1.前面的线性回归只有一个单一特征量，即房屋的面积大小x，我们希望用这个特征量来预测y值，即房屋的价格，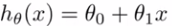
就是我们的假设函数。但是当我们有多个变量来来作为预测房屋的价格的一个特征或者一个变量，我们不仅知道了房屋的大小，还知道卧室的个数，楼层的数量以及房子的年龄，这就给了我们更多用来预测价格的信息。
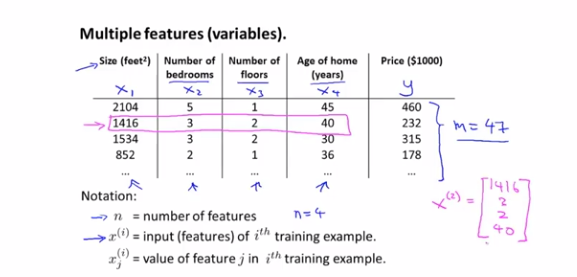
(1)我们在开始的时候提到过，要用这些变量，我们可以使用x1，x2，x3，x4等等来表示这四个特征，仍然用y来表示我们要预测的价格。
(2)n:表示特征量的数目
；x(i)：表示第i个训练样本的输入特征值，
比如x1表示第一个训练样本的特征向量，
,x1是我们用来预测第一个房子价格特征向量。
xij表示在第i个样本中的第j个特征向量的值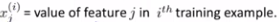
。比如：x(2)3表示第二个向量里第三个特征向量
2. 多个特征向量的特征表示式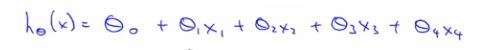
将所有的n个特征向量相加，比如一个房子的特征假设式为：
经过重写改写过的假设形式如下：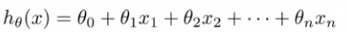
所以现在的特征向量x是一个从0开始标记的n+1维的向量
与此同时，我们将所有的参数都看做一个向量，也即将所有参数看成一个向量
对于这个式子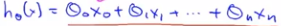
可以写成θ转置乘以X的形式，即
以上就是所谓的多元线性回归