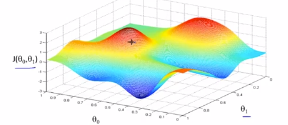
1.我们之前已经定义了代价函数J,可以将代价函数J最小化的方法,梯度下降是最常用的算法,它不仅仅用在线性回归上,还被应用在机器学习的众多领域中,在后续的课程中,我们将使用梯度下降算法最小化其他函数,而不仅仅是最小化线性回归的代价函数J。本节课中,主要讲用梯度下降的算法来最小化任意的函数J,下图是我们的问题:

(1)梯度下降的思路:
给定θ0和θ1的初始值,首先将θ0和θ1初始化为0,在梯度下降中我们要做的是不停的改变θ0和θ1,来使得J(θ0,θ1)变小,直到我们找到J的值的最小值或者局部最小值。
我们从θ0和θ1的某个值出发,对θ0和θ1赋以初值,就是对应于从下面这个函数的表面上某个点出发,一般情况下降θ0和θ1赋初值为0。
(2)梯度下降算法:

我们要更新参数θj,为θj减去α乘以这一部分,接下来详细解释该公式:
(1)赋值:符号 := 表示赋值,这是一个赋值运算符。具体的说,如果写成a:=b,在计算机中,表示不管a的原始值是是什么,将b赋值给a,这意味着我们设定a等于b的值,这就是赋值。
(2)α:α表示学习率,用来控制在梯度下降的时候,我们迈出多大的步子,α如果很大,那么梯度就下降的很迅速,我们就会用大步子下山;如果α值比较小,我们就会迈着很小的碎步下山
(3)θ0和θ1的更新,对于:
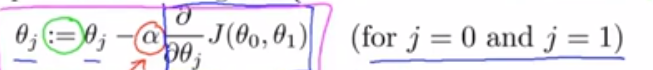
我们需要同时更新θ0和θ1,在这个式子中,就是讲θ0减去某项,将θ1减去某项,实现的方法是:计算右边的部分,对θ0和θ1进行计算,然后同时更新θ0和θ1,下面是正确的同步更新的方法。
