简要题意:
给定一个初始棋盘,每次一个马可以跳到空位(不考虑蹩腿问题)。求到达目标棋盘的最小步数。
本题其实是 八数码难题 的一个强化版,可以去看看 P1379 八数码难题 题解.
首先本题肯定是 搜索。
-
状态:棋盘压缩成字符串。
-
答案:记录步数。
-
如何实现:深度优先搜索,即 ( exttt{dfs}).
咦?( exttt{dfs}) 的效率不是严格不优于 ( exttt{bfs}) 的么?为什么还要用它呢?
嗯,只要我们加上一点点优化,( exttt{dfs}) 就不叫 ( exttt{dfs}) 了,它换了一个名字,叫做 ( ext{A*}) 算法;如果你再优化 亿点点,就可以再升级为 ( ext{IDA*}) 算法!
那么,这些优化是什么?为什么只有 ( exttt{dfs}) 才能用呢?而 ( ext{A* , IDA*}) 都是什么呢?
我们来一层层解决这个问题。
首先,我们画出一个搜索状态图(大概)。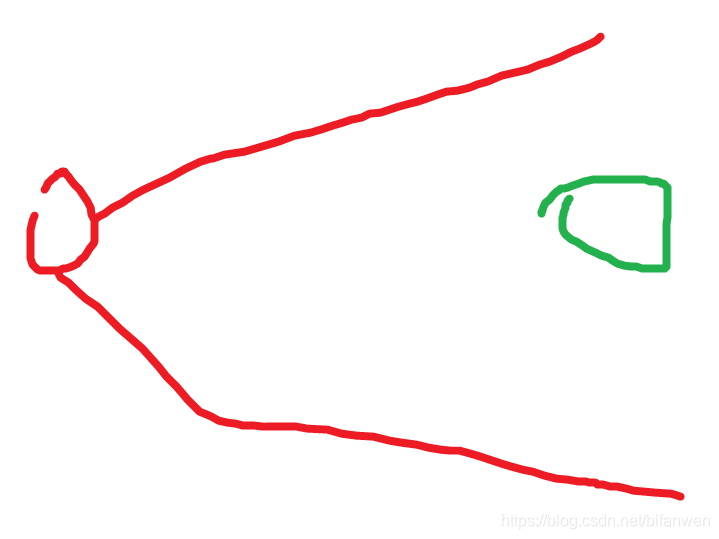
红色是起点状态,绿色是目标状态。在两红色轮廓线中的是我们要搜索的所有状态。
可是,你会发现有一些东西完全不用搜索。就比方说,如果跳了一步之后,反而比原来不跳更差了,那么这步就不用做了。
对,这就是一个有力的剪枝,这样的搜索方式被称为 ( ext{A*}).
那么,如果确定 当前状态的优劣性呢?
这时我们引进了 估价函数 (h) 的概念。
(h) 它的主要作用是估计当前状态到目标状态的步数。(与实际答案相差很大,但可作为参考)其特点在于,(h) 返回的是最小可能的步数,不可能从当前状态用 (<h) 步完成问题。
所以,如果当前状态为 (x),从起点走了 (g_x) 步到达 (x),然后其估价函数 咕值函数 为 (h_x),(f_x) 为起点的估价函数。此时我们力求满足:
此时搜索的效率就取决于 (h) 到底怎么写。如何快速估计最小步数?(小学数学估算题)
比方说,当前状态(左)与目标状态(右)如下:
1 1 1 1 1 -> 0 0 0 0 0
0 1 1 1 1 -> 1 0 0 0 0
0 0 * 1 1 -> 1 1 * 0 0
0 0 0 0 1 -> 1 1 1 1 0
0 0 0 0 0 -> 1 1 1 1 1
我们草率地估计,最少需要 (24) 步。为什么呢?
因为这两个状态有 (24) 个位置不同(除了空位都不同),那么 如果每一步都能让一个位置正确地归位(即达到目标状态),这样也需要 (24) 步才能让每个位置归位,这是我们能估算的较准确值了。 尽管与答案相差较大,但这是我们能估算的最大值了。
那么,如果当前走了一步之后有 (25) 个不同(就比方说你把 (1,2) 移到 (3,3) 空位上),那么这种搜索显然无效,只会变劣,直接停止。
所以你发现这个图如果用剪枝的话一步也走不了了(因为无论怎么走都是 (25) 个不同),返回无解。这比你 大力 ( ext{bfs}) 剪枝 要快得多吧!
下面我们引进 迭代加深搜索 的概念。
什么叫做迭代加深呢?
比方说,现在你可能搜索到的最大深度是 (10^9),但答案只有 (leq 10) 步,而宽度随着深度的增大也爆炸性增长. 此时,你无法用 ( ext{bfs}) 和 ( ext{dfs}) 任何一种解决。这时需要 迭代加深搜索。什么意思呢?
大概步骤是:
-
枚举当前深度(步数),进入 ( ext{dfs}).
-
如果当前搜索超过深度直接结束;否则向下一个状态搜索。
-
有解则结束返回当前深度;否则枚举下一个深度。
-
深度枚举到 一定范围 发现无解则返回无解。
也就是枚举搜索深度进行搜索,这样子一步步搜索,可以说是基于 ( ext{bfs}) 与 ( ext{dfs}) 之间的一种算法吧。
下面我们要将这两个算法结合,迭代加深搜索 与 ( ext{A*}) 结合就变成了 ( ext{IDA*}). 步骤:
-
枚举最大步数,进入 ( ext{A*}).
-
如果当前步数 (+ f) 值超过最大步数则结束;否则向下一个状态搜索。
-
有解则结束返回当前步数;否则枚举下一个步数。
-
步数枚举到 一定范围 发现无解则返回无解。
其实就是在 ( ext{A*}) 基础上限定深度,在 迭代加深搜索 上加一个有力剪枝。
那么,本题中这个 一定范围 是多少呢?其实你设成 (15) 就够了,因为题目说了:
如果能在 (15) 步以内(包括 (15) 步)到达目标状态,则输出步数,否则输出 (-1)。
如果最大步数超过 (15) 就不用再做了。
时间复杂度:(O(wys)).(很优却难以分析的复杂度一般这样称呼)
实际得分:(100pts).
#pragma GCC optimize(2)
#include<bits/stdc++.h>
using namespace std;
inline int read(){char ch=getchar();int f=1;while(ch<'0' || ch>'9') {if(ch=='-') f=-f; ch=getchar();}
int x=0;while(ch>='0' && ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x*f;}
int T,ans=1e9;
char end[6][6]={
{'1','1','1','1','1'},
{'0','1','1','1','1'},
{'0','0','2','1','1'},
{'0','0','0','0','1'},
{'0','0','0','0','0'},
} ; //结束状态
char a[6][6];
bool ok=0;
const int dx[8]={-2,-1,1,2,2,1,-1,-2};
const int dy[8]={-1,-2,-2,-1,1,2,2,1};
inline int g() {
int s=0; for(int i=0;i<5;i++)
for(int j=0;j<5;j++) s+=(a[i][j]!=end[i][j]);
return s;
} //不同的个数 , 即估价函数
inline void dfs(int dep,int x,int y,int bs) { //dep 是步数 , x 和 y 是空格位置(便于扩展状态) , bs 是当前枚举的最大步数
int t=g(); if(!t) {ok=1;return;} //如果完全相同则结束搜索
if(dep==bs) { //到达最大步数又没有到达终点 , 说明无解
return;
} for(int i=0;i<=8;i++) { //枚举马的走法
int nx=x+dx[i],ny=y+dy[i];
if(nx<0 || ny<0 || nx>4 || ny>4) continue;
swap(a[nx][ny],a[x][y]); //暴力交换
if(g()+dep<=bs) dfs(dep+1,nx,ny,bs); // A* 剪枝 , 进入下一层
swap(a[nx][ny],a[x][y]);
}
}
int main(){
T=read(); while(T--) {
int x,y; ok=0;
for(int i=0;i<5;i++) for(int j=0;j<5;j++) {
cin>>a[i][j];
if(a[i][j]=='*') x=i,y=j,a[i][j]='2';
} if(!g()) {puts("0");continue;} //不同的是 0 个 , 即起点与终点相同
for(int bs=1;bs<=15;bs++) { //迭代加深
dfs(0,x,y,bs); //枚举深度 , 进入 A*
if(ok) {printf("%d
",bs);goto fin;}
} puts("-1"); fin:;
}
return 0;
}
文末:还有一种非常卑鄙的优化,因为如果最后答案是 (-1) 时间较大(当然可以通过测试)而其余答案的耗时较小,采取 “只要程序执行超过某时间就返回 (-1) 的方式”,非常不严谨但很实用,可以大大提高效率。建议考试不要用,防止极限(如正好 (15) 步)数据。