多项式方程的输出

题目来源：https://www.luogu.org/problem/P1067

题目描述

一元nn次多项式可用如下的表达式表示：

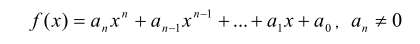
f(x)=a_nx^n+a_{n-1}x^{n-1}+cdots +a_1x+a_0,a_n e 0f(x)=an​xn+an−1​xn−1+⋯+a1​x+a0​,an​≠0

其中，a_ix^iai​xi称为ii次项，a_iai​ 称为ii次项的系数。给出一个一元多项式各项的次数和系数，请按照如下规定的格式要求输出该多项式：

1. 多项式中自变量为xx，从左到右按照次数递减顺序给出多项式。

2. 多项式中只包含系数不为00的项。

3. 如果多项式nn次项系数为正，则多项式开头不出现“+”号，如果多项式nn次项系数为负，则多项式以“-”号开头。

对于不是最高次的项，以“+”号或者“-”号连接此项与前一项，分别表示此项系数为正或者系数为负。紧跟一个正整数，表示此项系数的绝对值（如果一个高于00次的项，其系数的绝对值为11，则无需输出 11）。如果xx的指数大于11，则接下来紧跟的指数部分的形式为“x^bxb”，其中 bb为 xx的指数；如果 xx的指数为11，则接下来紧跟的指数部分形式为“xx”；如果 xx 的指数为00，则仅需输出系数即可。

多项式中，多项式的开头、结尾不含多余的空格。

输入格式

输入共有 22 行

第一行11 个整数，nn，表示一元多项式的次数。

第二行有 n+1n+1个整数，其中第ii个整数表示第n-i+1n−i+1 次项的系数，每两个整数之间用空格隔开。

输出格式

输出共 11 行，按题目所述格式输出多项式。

输入输出样例

输入 #1复制

5 
100 -1 1 -3 0 10

输出 #1复制

100x^5-x^4+x^3-3x^2+10

输入 #2复制

3 
-50 0 0 1 

输出 #2复制

-50x^3+1 

说明/提示

NOIP 2009 普及组 第一题

对于100%数据，0 le n le 1000≤n≤100,-100 le−100≤系数le 100≤100

#include<iostream>
#include<cstring>
using namespace std;

int main()
{ 
    int n,flag = 0;
    cin >> n;
    for(int i = n;i >= 0;i--)
    {
        int a;
        int temp = n;
        cin >> a;
        
        if(a == 0 || (a == 0 && i == 0))//系数为0或者系数为零同时0次幂为0时 
        {
            flag++;
            continue;
        }
        if(a > 0)//系数大于零时 
        {
            if(i == 0)//零次幂 
                cout << "+" << a;
            else if(i == n - flag)
                    if(a == 1)//最高次幂项的系数！！！并且系数为1时的情况，拎出来讨论 
                        cout << "x^" << i;//最高次幂项的系数 !!!!!!!!!!只需要执行一次！ 
                    else
                        cout << a << "x^" << i;//最高次幂项的系数！！！系数不为1时 
            else if(i == n - flag && a == 1)//非最高次幂项，系数为1时的情况 
                cout << "x^" << i;
            else if(i == 1 && a == 1)//系数和次幂均为一时 
                cout << "+x";
            else if(i == 1)//一次幂时且系数不为1时的情况 
                cout << "+" << a << "x";
            else if(a == 1)//系数为1时 
                cout << "+x^" << i;
            else
                cout << "+" << a << "x^" << i;//一般情况 
        }
        else
        {
            if(a < 0)//系数为负数的情况 
            {
                if(i == 0)
                    cout << a;
                else if(a == -1 && i == 1)
                    cout << "-x";
                else if(a == -1)
                    cout << "-x^" << i;
                else if(i == 1)
                    cout << a << "x";
                else
                    cout << a << "x^" << i;
            }
        }
    }
    if(flag == n + 1)//系数均为0时的情况 
        cout << "0";
    return 0;
}

/*
3
1 -100 0 0
*/

/*
3
0 0 0 1
*/

思路：切记将1与0拿出来分析，还有系数为“+”时的情况

此题不难，但是用这种方法的话绕的弯多，不是一个很好的题解，但可供参考