参考链接:http://dongxicheng.org/structure/union-find-set/ 作者Dong
算法介绍
LCA(Least Common Ancestors)问题的定义是这样的,给定2个点,求出离他们最近的也也就是深度最深(或者说是离树根最远的)的公共祖先。这个问题如果细细去想,也不算法是特别难的一个问题,最简单的办法就是,依次从2个点开始,往父亲节点上去寻找,如果存在2个父亲节点是一样的,这个父亲就是此2点的最近公共祖先。当然,这是最简单的也是很容易想到的方法。所以本文所描述的算法的执行效率当然是比这个要好很多的。LCA算法分为离线算法和在线算法2种。那么有人一定会想,他们之间的区别是什么呢,在线算法,顾名思义,就是请求数据输入一条,则输出一条结果,然后再输入一次请求查询,在输出结果,在线的意思,很好理解。而离线算法指的是一次性输入所有的请求查询条件,然后需要在算法执行结束的时候输出所有结果。因为平常说的比较多的是LCA的离线算法,所以今天我所写的也是LCA的求解的离线算法。
算法原理
LCA的离线算法采用的是Tarjan算法,Tarjan算法之前我也没有接触过,查了一下,是用来求有向图的强连通分量的。里面用了并查集和DFS深度优先算法的知识。DFS深度优先算法大家都知道是怎么回事,并查集估计听过的人不是很多。好,下面就先来介绍一下并查集的一些概念和操作。
并查集
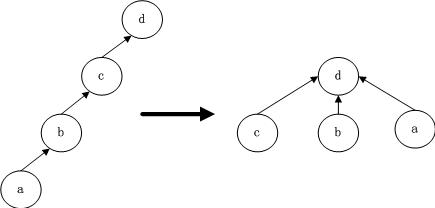
并查集操作主要有2个,1个是findSet(),用来查找节点的祖先的,祖先的特点是祖先的父亲等于他本身,以这个作为关键的判定条件,图示如下:
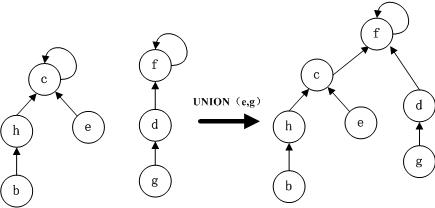
还有一个操作是unionSet(int a, int b),合并集合操作,找出2个节点的祖先,将其中的一个节点的祖先的父亲指向另一个节点。图示如下:
并查集的相关实现代码在后面的代码实现中会给出,请大家注意观察。
算法过程
算法的执行过程是采用DFS深度优先遍历的方式,每一次遍历完一个节点的时候,会重新将此点与父亲节点合并,这是算法的比较巧妙的操作。算法的执行非常的高,只要遍历过一遍整棵树,就能得到所有的结果,所有他的时间复杂度为O(n + q),n为节点总数,q为查询的数量,为线性级别。算法的伪代码如下:
LCA(u)
{
Make-Set(u)
ancestor[Find-Set(u)]=u
对于u的每一个孩子v
{
LCA(v)
Union(u)
ancestor[Find-Set(u)]=u
}
checked[u]=true
对于每个(u,v)属于Q
{
if checked[v]=true
then { 回答u和v的最近公共祖先为 ancestor[Find-Set(v)] }
}
}我在实现的时候略去了union下面的ancestor[Find-Set(u)] = u,这个操作我认为已经包含在union里面了,这点是我感觉比较费解的。下面给出算法的完整实现。
算法的实现
测试点数据dataFile:
1 2 3 4 5 6 7 8 9 10
为了准确测试遍历的整个过程,我列举了所有点构成查询对的可能,也就是是说有9 + 8 + 7 + .... + 1 = 45种可能。
1 2
1 3
1 4
1 5
1 6
1 7
1 8
1 9
1 10
2 3
2 4
2 5
2 6
2 7
2 8
2 9
2 10
3 4
3 5
3 6
3 7
3 8
3 9
3 10
4 5
4 6
4 7
4 8
4 9
4 10
5 6
5 7
5 8
5 9
5 10
6 7
6 8
6 9
6 10
7 8
7 9
7 10
8 9
8 10
9 10
package LCA;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;
import java.text.MessageFormat;
import java.util.ArrayList;
import java.util.concurrent.LinkedBlockingQueue;
/**
* LCA最近公共祖先算法
*
* @author lyq
*
*/
public class LCATool {
// 节点数据文件
private String dataFilePath;
// 查询请求数据文件
private String queryFilePath;
// 节点祖先集合,数组下标代表所对应的节点,数组组为其祖先值
private int[] ancestor;
// 标记数组,代表此节点是否已经被访问过
private boolean[] checked;
// 请求数据组
private ArrayList<int[]> querys;
// 请求结果值
private int[][] resultValues;
// 初始数据值
private ArrayList<String> totalDatas;
public LCATool(String dataFilePath, String queryFilePath) {
this.dataFilePath = dataFilePath;
this.queryFilePath = queryFilePath;
readDataFile();
}
/**
* 从文件中读取数据
*/
private void readDataFile() {
File file = new File(dataFilePath);
ArrayList<String[]> dataArray = new ArrayList<String[]>();
try {
BufferedReader in = new BufferedReader(new FileReader(file));
String str;
String[] tempArray;
while ((str = in.readLine()) != null) {
tempArray = str.split(" ");
dataArray.add(tempArray);
}
in.close();
} catch (IOException e) {
e.getStackTrace();
}
totalDatas = new ArrayList<>();
for (String[] array : dataArray) {
for (String s : array) {
totalDatas.add(s);
}
}
checked = new boolean[totalDatas.size() + 1];
ancestor = new int[totalDatas.size() + 1];
// 读取查询请求数据
file = new File(queryFilePath);
dataArray.clear();
try {
BufferedReader in = new BufferedReader(new FileReader(file));
String str;
String[] tempArray;
while ((str = in.readLine()) != null) {
tempArray = str.split(" ");
dataArray.add(tempArray);
}
in.close();
} catch (IOException e) {
e.getStackTrace();
}
int x = 0;
int y = 0;
querys = new ArrayList<>();
resultValues = new int[dataArray.size()][dataArray.size()];
for (int i = 0; i < dataArray.size(); i++) {
for (int j = 0; j < dataArray.size(); j++) {
// 值-1代表还未计算过LCA值
resultValues[i][j] = -1;
}
}
for (String[] array : dataArray) {
x = Integer.parseInt(array[0]);
y = Integer.parseInt(array[1]);
querys.add(new int[] { x, y });
}
}
/**
* 构建树结构,此处默认构造成二叉树的形式,真实情况根据实际问题需要
*
* @param rootNode
* 根节点参数
*/
private void createTree(TreeNode rootNode) {
TreeNode tempNode;
TreeNode[] nodeArray;
ArrayList<String> dataCopy;
LinkedBlockingQueue<TreeNode> nodeSeqs = new LinkedBlockingQueue<>();
rootNode.setValue(Integer.parseInt(totalDatas.get(0)));
dataCopy = (ArrayList<String>) totalDatas.clone();
// 移除根节点的首个数据值
dataCopy.remove(0);
nodeSeqs.add(rootNode);
while (!nodeSeqs.isEmpty()) {
tempNode = nodeSeqs.poll();
nodeArray = new TreeNode[2];
if (dataCopy.size() > 0) {
nodeArray[0] = new TreeNode(dataCopy.get(0));
dataCopy.remove(0);
nodeSeqs.add(nodeArray[0]);
} else {
tempNode.setChildNodes(nodeArray);
break;
}
if (dataCopy.size() > 0) {
nodeArray[1] = new TreeNode(dataCopy.get(0));
dataCopy.remove(0);
nodeSeqs.add(nodeArray[1]);
} else {
tempNode.setChildNodes(nodeArray);
break;
}
tempNode.setChildNodes(nodeArray);
}
}
/**
* 进行lca最近公共祖先算法的计算
*
* @param node
* 当前处理的节点
*/
private void lcaCal(TreeNode node) {
if (node == null) {
return;
}
// 处理过后的待删除请求列表
ArrayList<int[]> deleteQuerys = new ArrayList<>();
TreeNode[] childNodes;
int value = node.value;
ancestor[value] = value;
childNodes = node.getChildNodes();
if (childNodes != null) {
for (TreeNode n : childNodes) {
lcaCal(n);
// 深度优先遍历完成,重新设置祖先值
value = node.value;
//通过树型结构进行祖先的设置方式,易于理解
// setNodeAncestor(n, value);
if(n != null){
//合并2个集合
unionSet(n.value, value);
}
}
}
// 标记此点被访问过
checked[node.value] = true;
int[] queryArray;
for (int i = 0; i < querys.size(); i++) {
queryArray = querys.get(i);
if (queryArray[0] == node.value) {
// 如果此时另一点已经被访问过
if (checked[queryArray[1]]) {
resultValues[queryArray[0]][queryArray[1]] = findSet(queryArray[1]);
System.out.println(MessageFormat.format(
"节点{0}和{1}的最近公共祖先为{2}", queryArray[0],
queryArray[1],
resultValues[queryArray[0]][queryArray[1]]));
deleteQuerys.add(querys.get(i));
}
} else if (queryArray[1] == node.value) {
// 如果此时另一点已经被访问过
if (checked[queryArray[0]]) {
resultValues[queryArray[0]][queryArray[1]] = findSet(queryArray[0]);
System.out.println(MessageFormat.format(
"节点{0}和{1}的最近公共祖先为{2}", queryArray[0],
queryArray[1],
resultValues[queryArray[0]][queryArray[1]]));
deleteQuerys.add(querys.get(i));
}
}
}
querys.removeAll(deleteQuerys);
}
/**
* 寻找节点x属于哪个集合,就是寻找x的最早的祖先
*
* @param x
*/
private int findSet(int x) {
// 如果祖先不是自己,则继续往父亲节点寻找
if (x != ancestor[x]) {
ancestor[x] = findSet(ancestor[x]);
}
return ancestor[x];
}
/**
* 将集合x所属集合合并到y集合中
*
* @param x
* @param y
*/
public void unionSet(int x, int y) {
// 找到x和y节点的祖先
int ax = findSet(x);
int ay = findSet(y);
// 如果2个祖先是同一个,则表示是同一点,直接返回
if (ax != ay) {
// ax的父亲指向y节点的祖先ay
ancestor[ax] = ay;
}
}
/**
* 设置节点的祖先值
*
* @param node
* 待设置节点
* @param value
* 目标值
*/
private void setNodeAncestor(TreeNode node, int value) {
if (node == null) {
return;
}
TreeNode[] childNodes;
ancestor[node.value] = value;
// 递归设置节点的子节点的祖先值
childNodes = node.childNodes;
if (childNodes != null) {
for (TreeNode n : node.childNodes) {
setNodeAncestor(n, value);
}
}
}
/**
* 执行离线查询
*/
public void executeOfflineQuery() {
TreeNode rootNode = new TreeNode();
createTree(rootNode);
lcaCal(rootNode);
System.out.println("查询请求数剩余总数" + querys.size() + "条");
}
}
package LCA;
/**
* 树结点类
* @author lyq
*
*/
public class TreeNode {
//树结点值
int value;
//孩子节点,不一定只有2个节点
TreeNode[] childNodes;
public TreeNode(){
}
public TreeNode(int value){
this.value = value;
}
public TreeNode(String value){
this.value = Integer.parseInt(value);
}
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
public TreeNode[] getChildNodes() {
return childNodes;
}
public void setChildNodes(TreeNode[] childNodes) {
this.childNodes = childNodes;
}
}
package LCA;
/**
* LCA最近公共祖先算法测试类
* @author lyq
*
*/
public class Client {
public static void main(String[] args){
//节点数据文件
String dataFilePath = "C:\Users\lyq\Desktop\icon\dataFile.txt";
//查询请求数据文件
String queryFilePath = "C:\Users\lyq\Desktop\icon\queryFile.txt";
LCATool tool = new LCATool(dataFilePath, queryFilePath);
tool.executeOfflineQuery();
}
}
节点8和9的最近公共祖先为4
节点4和8的最近公共祖先为4
节点4和9的最近公共祖先为4
节点4和10的最近公共祖先为2
节点8和10的最近公共祖先为2
节点9和10的最近公共祖先为2
节点4和5的最近公共祖先为2
节点5和8的最近公共祖先为2
节点5和9的最近公共祖先为2
节点5和10的最近公共祖先为5
节点2和4的最近公共祖先为2
节点2和5的最近公共祖先为2
节点2和8的最近公共祖先为2
节点2和9的最近公共祖先为2
节点2和10的最近公共祖先为2
节点2和6的最近公共祖先为1
节点4和6的最近公共祖先为1
节点5和6的最近公共祖先为1
节点6和8的最近公共祖先为1
节点6和9的最近公共祖先为1
节点6和10的最近公共祖先为1
节点2和7的最近公共祖先为1
节点4和7的最近公共祖先为1
节点5和7的最近公共祖先为1
节点6和7的最近公共祖先为3
节点7和8的最近公共祖先为1
节点7和9的最近公共祖先为1
节点7和10的最近公共祖先为1
节点2和3的最近公共祖先为1
节点3和4的最近公共祖先为1
节点3和5的最近公共祖先为1
节点3和6的最近公共祖先为3
节点3和7的最近公共祖先为3
节点3和8的最近公共祖先为1
节点3和9的最近公共祖先为1
节点3和10的最近公共祖先为1
节点1和2的最近公共祖先为1
节点1和3的最近公共祖先为1
节点1和4的最近公共祖先为1
节点1和5的最近公共祖先为1
节点1和6的最近公共祖先为1
节点1和7的最近公共祖先为1
节点1和8的最近公共祖先为1
节点1和9的最近公共祖先为1
节点1和10的最近公共祖先为1
查询请求数剩余总数0条
我对算法的理解
LCA离线算法最大的奇妙之处在于,他用了并查集的相关知识,使得算法的时间复杂度优化了很多,但在最开始的时候我用的是通过判断树形结构来设定祖先,这样是比较好理解的,但是效率比较低,要一遍遍的遍历。如果大家暂时不理解并查集的函数操作,可以看看被我注释掉的setNodeAncestor(),,二者所要做的事情是一样的。LCA算法的特点在于并查集,所以我还是用了并查集的方法去实现。