动态规划入门秘籍

　　最近在学习DP，心里就一个感觉，难，这几天上课比较忙，就利用一些空闲时间看了n遍算法导论和n遍白书上面有关Dp的章节，现在感觉自己......萌萌哒......

　　回归正题，其实收获还是有一些的，今天准备开始做一些动态规划的入门级的水题...

　　先来让dsy大佬带领大家认识一下dp...脸黑.jpg

　　DP问题需要满足两个基本条件，即有相同的重叠子问题和最优子结构，听我下面详细道来(其实是抄袭西工大dsy大佬的呜呜呜......)......小声bb.jpg

　　关于最优子结构：

　　

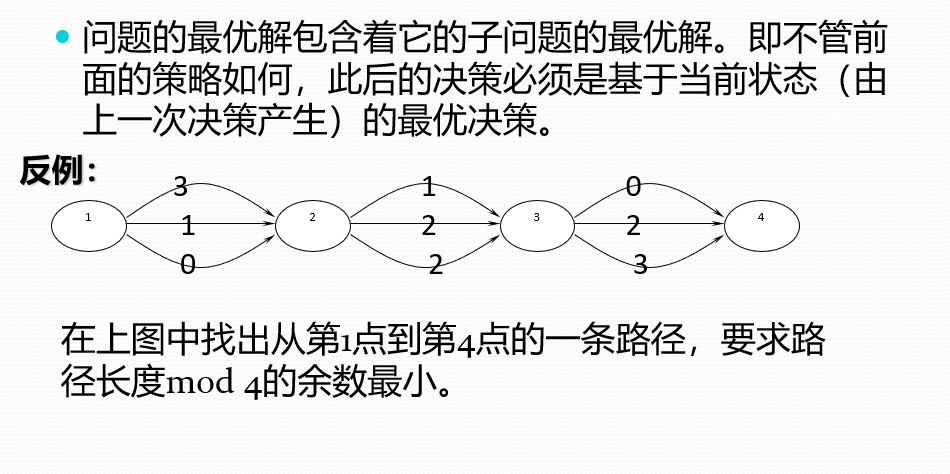
　　关于重叠子问题

下面是dsy大佬给出的DP一般做题思路：

 

先来看一些简单的入门级DP问题吧...

 

①：爬楼梯

　　给一个leetcode上面的题目链接吧:大体意思就是给你n阶台阶，每次只能上一格或者两格，问你共有多少种办法从第零层开始爬完整个楼梯。

　　这道题是很基础的DP问题，首先我们找出这个问题的最优子结构和重叠子问题，这个问题我自我赶脚没有最优子结构，因为这不是最优问题...但是具有重叠子问题，下面展开来说。

　　假设你现在正在第n阶台阶，你只需考虑你是如何到达这个台阶的，有两种方法就是从第n-1 或n-2 跨上来的,对于n - 1  和 n - 2 进行同样的思考，

　　n -------- n - 1 和  n - 2

　　n - 1 ---------- n - 2 和 n - 3

　　n - 2 -----------n - 3 和n - 4

　　...

　　...

　　...

　　第二层有2种方法，第一层只有1种方法

　　由上式很容易可以看出动态转移方程为dp[n] = dp[n - 1] + dp[n - 2], dp[1] = 1, dp[2] = 2。

　　参考代码：

#include <iostream>
#include <cstring>
using namespace std;

const int maxn = 1e6 + 5;
int dp[maxn];

int climbing (int n) {
    if(n == 1) return 1;
    if(n == 2) return 2;
    if(dp[n] != 0) return dp[n];
    return dp[n] = climbing(n - 1) + climbing(n - 2);
}

int main () {
    memset(dp, 0, sizeof dp);
    int n, ans;
    cin >> n;
    ans = climbing(n);
    cout << ans << endl;
    return 0;
}

②：最长不下降子序列（LIS）

　　一个经典的dp问题，题意就是给定你一个n长的数列，让你求出最长不下降子序列的长度。

　　这道题乍一看就想暴力，但是现在在学DP.....，下面展开来说。

　　我们依然从最特殊的第n个数开始看起，易得dp[ n ] = dp[n - 1] + 1（s[n - 1] <= s[n]）, 此时dp[ i ]表示以i为结尾的LIS，可以得出一个递推方程：dp[ i ] = max(dp[ i ], dp [ j ] + 1)(j < i)，初始dp[ i ]为1，下面给出两种写法，没有用单调队列优化。

参考代码：

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int maxn = 1e4;
int dp[maxn];
int a[] = {1, 2, 3, 2, 5, 8, 4, 3, 8, 2, 45, 23, 234, 23, 34, 235, 234, 5324,};
int n = sizeof a / sizeof a[0],  ans = 0;

int calcu1() {
    ans = 0;
    for(int i = 0; i < n; i ++) {
        dp[i] = 1;
        for(int j = 0; j < i; j ++) 
            if(a[j] <= a[i])
                dp[i] = max(dp[i], dp[j] + 1);
        ans = max(ans, dp[i]);
    }
    return ans;
}

int calcu2(int x) {
    if(dp[x] != 0) return dp[x];
    dp[x] = 1;
    for(int i = 0; i < x; i ++) {
        if(a[i] <= a[x]) {
            ans = calcu2(i);
            if(ans + 1 > dp[x]) dp[x] = ans + 1;
        }
    }
    return dp[x];
}

int main () {
    ans = calcu1();
    cout << ans << endl;
    ans = calcu2(n - 1);
    cout << ans << endl;
    return 0;
}

 

　　上面代码的复杂度为O(n^2)，那么有没有办法进行优化呢，有的...

　　我们可以重新考虑一下如何优化呢，我们想到如果用dp[ i ]表示长度为i的子序列的最后一个元素，那么我们每插入一个元素，都只需要找到第一个大于他的元素的位置，然后将其插入即可。刚好查找函数upper_bound复杂度为logn，那么具体就见代码咯...

单调队列优化代码：

int my_upper_bound(int left, int right, int x) {
    int mid;
    while(left <= right) {
        mid = left + (right - left) / 2;
        if(dp[mid] > a[x]) right = mid - 1;
        else left = mid + 1;
    }
    return left;
}

int calcu3() {
    int num = 1;
    dp[num] = a[0];
    for(int i = 1; i < n; i ++) {
        if(a[i] >= dp[num]) dp[++ num] = a[i];
        else dp[my_upper_bound(0, num, i)] = a[i];
        // else dp[upper_bound(dp + 1, dp + num + 1, a[i]) - dp] = a[i]; 
    }
    return num;
}

 　　那么要如何证明这样的重叠子问题是正确的呢，下面做详细解释吧......

　　用dp[ i ]表示长度为i的自序列的末尾元素，那么要如何证明dp[ i ]中的元素会随着 i 的增大而非递减呢，首先我们将第一个元素放入

dp[ 1 ]中，接着对随后的每个元素进行判断，如果当前元素不小于目前最长子序列的最后一个元素，就说明它会构成一个更长的

不下降子序列，那么我们就可以考虑直接将它存到dp[i + 1]中，否则我们就在当前已经存好的每个长度对应的所有元素中从前往后找，

保证了改数保存到了第一个大于它的序列中，这样的存储结构直接就可以将dp中的所有元素按照非递减的顺序排列起来。

③：数字三角形

　　这也是一个经典的二维DP的问题，假设dp[ i ] [ j ] 表示第 i 层在第 j 列的值，则dp[ i ] [ j ] 可以由 dp[i - 1][ j ] 和 dp[ i - 1] [j - 1]计算的来。

可得状态转移方程为dp[ i ] [ j ] = max (dp[i - 1][ j ] , dp[ i - 1] [j - 1]) + a[ i ][ j ]。

参考代码：

#include <iostream>
using namespace std;

const int maxn = 100 + 5;
int a[maxn][maxn], dp[maxn][maxn];

int main () {
    int n, num = 0, ans;
    cin >> n;
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= i; j ++)
            cin >> a[i][j];
    dp[1][1] = a[1][1];
    ans = dp[1][1];
    for(int i = 2; i <= n; i ++) {
        for(int j = 1; j <= i; j ++) {
            dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1]) + a[i][j];
            ans = max(ans, dp[i][j]);
        }
    }
    cout << ans << endl;
    return 0;
}

④：最长公共子序列

　　一个经典的DP问题，很显然它具有最优子结构，我们可以用dp[ i ][ j ]来表示分别在s1和s2中以 i 和 j 结尾的子串的公共子序列的长度，很容易可以得出dp[i + 1][j + 1]只会由dp[ i ][ j ]和dp[i + 1][ j ] 和dp[ i ][j + 1]中的一种的来，那么我们就可以得到状态转移方程，具体见代码咯。

#include <iostream>
#include <cstring>
using namespace std;

const int maxn = 1000;
char s1[maxn], s2[maxn];
int n, m;
int dp[maxn][maxn];

void solve() {
    for(int i = 0; i < n; i ++) 
        for(int j = 0; j < m; j ++) {
            if(s1[i] == s2[j]) dp[i + 1][j + 1] = dp[i][j] + 1;
            else dp[i + 1][j + 1] = max(dp[i + 1][j], dp[i][j + 1]);
        }
    cout << dp[n][m] << endl;
}

int main () {
    dp[0][0] = 0;
    while(cin >> s1 >> s2) {
        n = strlen(s1), m = strlen(s2);
        solve();
    }
    return 0;
}

后续更新dp题目，是时候暴露思维了......傲娇.jpg