几个基本概念
不包含任何结点的二叉树为空树
只包含一个结点的二叉树是一棵单点树
一棵二叉树可以包含任意(有穷个)个结点
一棵二叉树的根结点称为该树的子树根结点的父结点;与之对应,子树的根结点称为二叉树树根结点的子结点
父结点相同的两个结点称为兄弟结点,在二叉树中有些结点的两棵子树都空,没有子结点,这种结点称为树叶。树中其余结点称为分支几点。一个结点的子结点个数称为该结点的度数
一棵二叉树只能有五种形态:空二叉树;只有根结点;只有根结点和左子树;只有根结点和右子树;或者两棵子树俱全。
首尾相连的边称为树中的一条路径,路径汇总的边数称为该路径的长度;从一棵二叉树的根结点到该树中的任一结点都有路径,而且唯一。
二叉树是一种层次结构,从树根到树中任一结点的路径长度就是该结点所在的层数。一个二叉树的高度是树中结点的最大层数
满二叉树:如果二叉树中所有分支结点的度数都是2,则称他为一棵满二叉树。满二叉树里的叶结点比分支结点多一个
扩充二叉树:扩充二叉树中新增的结点称其为外部结点,原树的结点称为内部结点
完全二叉树:对于一个高为h的二叉树,如果其第0层至第h - 1 层的结点都满。如果最下一层的结点不满,则所有结点在最左边连续排列,空位都在右边。这样的二叉树是一棵完全二叉树。
二叉树的性质:
二叉树最重要的性质就是树的高度和树中可以容纳的最大结点输之间的关系。在肠胃n的表里只能容纳n个结点,里面搞为h的二叉树中则可能容纳大约n**h个结点,这是表与树的最大不同
性质:在飞空二叉树第i层中之多有2**i个结点(i>=0)
性质:高度为h的二叉树之多有(2**k-1) - 1 个结点
性质:对于任何非空二叉树T,如果其叶结点的个数n0,度数为2的结点度数为n2,那么 n0 = n2 + 1
性质:(完全二叉树)n个结点的完全二叉树高度为h = 【log2n】,即为不大于log2n 的最大整数
性质:(完全二叉树)如果n个结点的完全二叉树的结点按层次并按从左到右的顺序崇0开始编号,对任一结点i都有:
序号为0的结点是根
对于i>0,其腹肌诶单的编号是(i-1)/2
若2 x i + 2 < n,其左子结点序号为 2 x i+ 1,否则他无左子结点
若2 x i + 2 < n,其右子结点序号为 2 x i+ 2,否则他无右子结点
遍历二叉树
每棵二叉树都有唯一的根结点,可看做这个二叉树的唯一标示,也是处理树结构的入口。遍历二叉树一般存在两种方式:深度优先遍历,广度优先遍历
深度优先遍历:
需要做的三件事:遍历左子树,遍历右子树和访问根结点,以L,R,D为例
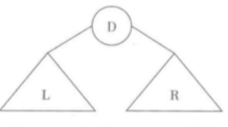
常见的三种遍历顺序:
先根序遍历(DLR)
中根序遍历(LDR)
后根序遍历(LRD)
示例:
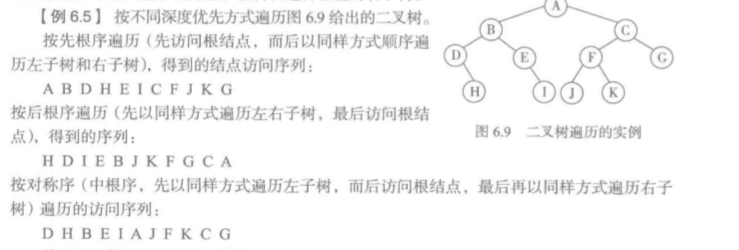
宽度优先遍历
宽度优先是按路径长度由近到远的访问(不能写成递归的过程),实现这一算法需要一个队列作为缓存
上图按宽度优先遍历的序列为:A B C D E F G H I J K