1.条件概率
事件A和事件B 事件A发生的前提下事件B发生的概率: P(AB) = P(B|A)P(A)
举例:
十个球其中 3 黑 7白,做两次不放回的取球,求两次都拿到黑球的概率(事件A为第一次取,事件B为第二次取。)
事件A 发生的概率 P(A) = 3/7,事件A发生的前提下B发生的概率: P(B|A) = 2/6
此时P(AB) = P(B|A)*P(A)
2.贝叶斯
贝叶斯公式:P(A|B) = P(B|A) * P(A) / P(B)
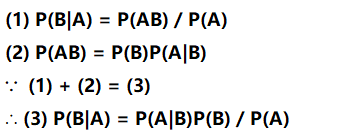
3.朴素贝叶斯
朴素贝叶斯分类是一种十分简单的分类算法,朴素贝叶斯的思想基础是这样的:对于给出的待分类项,求解在此项出现的条件下各个类别出现的概率,哪个最大,就认为此待分类项属于哪个类别。通俗来说,就好比这么个道理,你在街上看到一个黑人,我问你你猜这哥们哪里来的,你十有八九猜非洲。为什么呢?因为黑人中非洲人的比率最高,当然人家也可能是美洲人或亚洲人,但在没有其它可用信息下,我们会选择条件概率最大的类别,这就是朴素贝叶斯的思想基础。
假设给定x 判断 x 属于集合C中哪个y

其中p(x)是个给定的,所以 p(y | x) 正比于其分母项

4、朴素贝叶斯模型
朴素贝叶斯常用的三个模型有:
高斯模型:处理特征是连续型变量的情况
多项式模型:最常见,要求特征是离散数据
伯努利模型:要求特征是离散的,且为布尔类型,即true和false,或者1和0
5、贝叶斯算法使用示例
医院早上的六个病人情况如下:

现在又来了第七个病人,是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大?
求: p(感冒|工人, 打喷嚏) = p(工人, 打喷嚏|感冒) * p(感冒) / p(工人,打喷嚏)
= p(工人|感冒) * P(打喷嚏|感冒) * p(感冒) / p(工人) * p(打喷嚏)
= (1/3 * 2/3 * 3/6) / (2/6) * (3/6)
= 2/3