hdu1506——Largest Rectangle in a Histogram

Largest Rectangle in a Histogram

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 12019    Accepted Submission(s): 3326

Problem Description

A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:

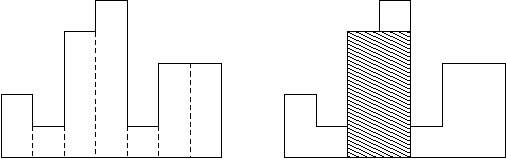
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

 

Input

The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1 <= n <= 100000. Then follow n integers h1, ..., hn, where 0 <= hi <= 1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.

 

Output

For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.

 

Sample Input

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

 

Sample Output

8
4000

 

Source

University of Ulm Local Contest 2003

 

Recommend

LL   |   We have carefully selected several similar problems for you:  1505 1058 1203 2870 1864

每一块木板的作用范围就夹在左右两边分别比他矮的木板之间。所以我们能够迭代地预处理出这两块木板的位置，之后仅仅须要for一遍就可以得到最大面积

一開始用递归的写法一直错，后来干脆改成非递归的了

#include <map>
#include <set>
#include <list>
#include <stack>
#include <queue>
#include <vector>
#include <cmath>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;
__int64 h[N];
int lp[N];
int rp[N];
int n;

int main()
{
    while (~scanf("%d", &n), n)
    {
        __int64 ans = 0;
        for (int i = 1; i <= n; ++i)
        {
            scanf("%I64d", &h[i]);
            ans = max(ans, h[i]);
        }
        lp[1] = 1;
        rp[n] = n;
        for (int i = 2; i <= n; ++i)
        {
            int p = i;
            while (p > 1 && h[i] <= h[p - 1])
            {
                p = lp[p - 1];
            }
            lp[i]= p;
        }
        for (int i = n - 1; i >= 1; --i)
        {
            int p = i;
            while (p < n && h[i] <= h[p + 1])
            {
                p = rp[p + 1];
            }
            rp[i]= p;
        }
/*        for (int i = 1; i <= n; ++i)
        {
           printf("%d ", lp[i]); 
        }
        printf("
");
        for (int i = 1; i <= n; ++i)
        {
           printf("%d ", rp[i]); 
        }
        printf("
");*/
        for (int i = 1; i <= n; ++i)
        {
            int l = lp[i];
            int r = rp[i];
            ans = max(ans, (r - l + 1) * h[i]);
        }
        printf("%I64d
", ans);
    }
    return 0;
}