机器学习的初步介绍，简单的线性回归问题时间，梯度下降的介绍

Tom Mitchell, 1996: Machine learning is the study of how to make programs improve their performance on certain tasks from (own) experience.机器学习是用数据或以往的经验,以此优化计算机程序的性能标准。这里面性能标准可以是速度、准确率，而以往的经验则就是数据。

一般机器学习的问题分为两大类，但是不论是分类还是回归，我们最终学习的都是一个函数：

回归问题：最后结果是一个数值

 分类问题：最后结果是一个类别

假定我已有数据集制图如下：

 

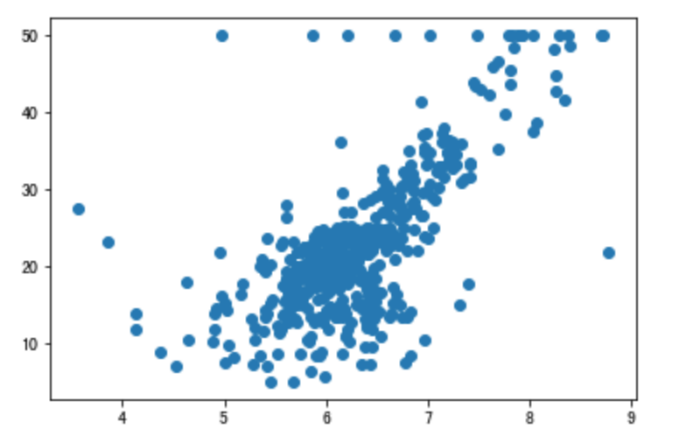
按我们回归问题的思路，现在我需要找到一个函数来拟合上面我原有的数据集，以方便后面预测新值。

那么我们如何找到最优函数？在这个函数由于x是给定的，那么其实我们需要调整的就是k与b的值。

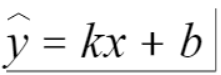
既然有调整那么肯定是有评测指标的，如何验证我的k、b是好是坏？我们可以计算我们以当前k、b计算出的值与数据集原真实值的误差是多少，然后取平均值，当这个误差最小时，则说明我们的k、b已经取到最优了。

在这里我们取的是预测值与真实值的误差平方，也可以用其他的方式，比如计算绝对值。

那么如何快速计算这个loss值呢？我们就需要要用到梯度下降方法。

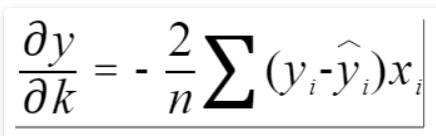
我们按照这个思路以自带数据集波士顿放假预测为例，以房间数设置为x，房间售价则是y实现代码如下：

#!/usr/bin/env python
# __author__ = '北方姆Q'
# -*- coding: utf-8 -*-


import random
from sklearn.datasets import load_boston


data_set = load_boston()
x, y = data_set['data'], data_set['target']
X_rm = x[:, 5]


def price(rm, k, b):
    return k * rm + b


def loss(y, y_hat):
    """
    绝对值平均
    :param y:
    :param y_hat:
    :return:
    """
    return sum((y_i - y_hat_i)**2 for y_i, y_hat_i in zip(list(y), list(y_hat)))/len(list(y))


def partial_derivative_k(x, y, y_hat):
    """
    k的导数
    :param x:
    :param y:
    :param y_hat:
    :return:
    """
    n = len(y)
    gradient = 0
    for x_i, y_i, y_hat_i in zip(list(x), list(y), list(y_hat)):
        gradient += (y_i-y_hat_i) * x_i
    return -2 * gradient / n


def partial_derivative_b(y, y_hat):
    """
    b的导数
    :param y:
    :param y_hat:
    :return:
    """
    n = len(y)
    gradient = 0
    for y_i, y_hat_i in zip(list(y), list(y_hat)):
        gradient += (y_i-y_hat_i)
    return -2 * gradient / n


def boston_loss():
    k = random.random() * 200 - 100
    b = random.random() * 200 - 100

    learning_rate = 1e-3

    iteration_num = 1000000
    losses = []
    for i in range(iteration_num):
        price_use_current_parameters = [price(r, k, b) for r in X_rm]

        current_loss = loss(y, price_use_current_parameters)
        losses.append(current_loss)
        print("Iteration {}, the loss is {}, parameters k is {} and b is {}".format(i, current_loss, k, b))

        k_gradient = partial_derivative_k(X_rm, y, price_use_current_parameters)
        b_gradient = partial_derivative_b(y, price_use_current_parameters)

        k = k + (-1 * k_gradient) * learning_rate
        b = b + (-1 * b_gradient) * learning_rate
    best_k = k
    best_b = b

boston_loss()