动态规划方法通常用来求解最优化问题。
适合使用动态规划求解最优化问题应具备的两个要素:
1、最优子结构:如果一个问题的最优解包含子问题的最优解,那么该问题就具有最优子结构。
2、子问题重叠(如果子问题不重叠就可以用递归的方法解决了)
具备上述两个要素的问题之所以用动态规划而不用分治算法是因为分治算法会反复的调用重叠的子问题导致,效率低下,而动态规划使用了运用了空间置换时间的思想,将每一个已解决的子问题保存起来,这样重复的子问题只需要计算1次,所以时间效率较高。
动态规划算法设计步骤:
1.刻画一个最优解的结构特征。
2.递归定义最优解的值。
3.计算最优解的值,通常采用自底向上的方法。
4.利用计算出的信息构造一个最优解。
其中发掘最优子结构的过程遵循下面的通用模式:
1. 证明问题最优解的第一个组成部分是做出一个选择。
2.
对于给定问题,在其可能的第一步选择中,假定已经知道哪种选择才会得到最优解,但并不关心这种选择具体是如何得到的,只是假定已经知道了这种选择。
3.
给定可获得最优解的选择后,确定这次选择会产生哪些子问题,以及如何最好地刻画子问题空间。
4. 利用
“剪切-粘贴”(cut-and-paste)技术证明:作为构成原问题最优解的组成部分,每个子问题的解就是它本身的最优解(利用反证法)。
动态规划的实现方法:
带备忘的自顶向下法:此方法仍按自然的递归形式编写过程,但过程会保存每个子问题的解(通常保存在一个数组或散列表中)。当需要一个子问题的解时,过程首先检查是否已经保存过此解。如果是,则直接返回保存的值,从而提高时间效率。
自底向上法:这种方法一般需要恰当定义子问题“规模”的概念,使得任何子问题的求解都依赖于“更小的”子问题的求解。因而我们可以将子问题按规模排序,按由小至大的顺序进行求解。当求解某个子问题时,它所依赖的那些更小的子问题都已经求解完毕,结果已经保存。每个子问题只需要求解一次,当我们求解它(也是第一次遇到它)时,它的所有前提子问题都已求解完成。
下面应用动态规划解决一个问题
serling公司购买长钢条,将其切割为锻钢条出售。切割工序没有成本。先给出出售一段长度为i的钢条的价格为p(i),对应关系如下表,求给一段长度为n(n<=10)的钢条,要切割多少次才能以最高的价格卖出?
| 长度i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 价格p(i) | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
首先这个问题求解要多少次才能以最高的价格卖出,是一个求最优化的问题,接下来分析下该问题是否具有适用于最优化问题的两个特征,假设n=5的话,要求解长度为5的钢条怎么切割才能获得最优解,首先我们知道将长度为5的钢条进行切割,第一刀可以选择0+5、1+4、2+3三种切割方案,然后在每一种切割方案中,将剩下的继续选择最优方案(和递归的思想一样,将原问题转换成更小的子问题),可以列出下列关系式:r(5)=max{p(1)+r(5-1),p(2)+r(5-2),p(3)+r(5-3),p(4)+r(5-4),p(5)+r(0)} 式中r(i)表示总长度为i时的最大收益。可以看出求解r(5)的最优解包含了求解其子问题r(4)、r(3)、r(2)、r(1)、r(0)的最优解,
更为通用的表达式就是r(n)=max{p(1)+r(n-1),p(2)+r(n-2),......p(n-1)+r(1),p(n)+r(0)}可以看出通用的表达式里面的最优解包含了其子问题的最优解,所以该问题符合最优子结构的特征,然后再看有没有第二个特征,还是以n=5进行分析,下图显示了求解子问题的递归树
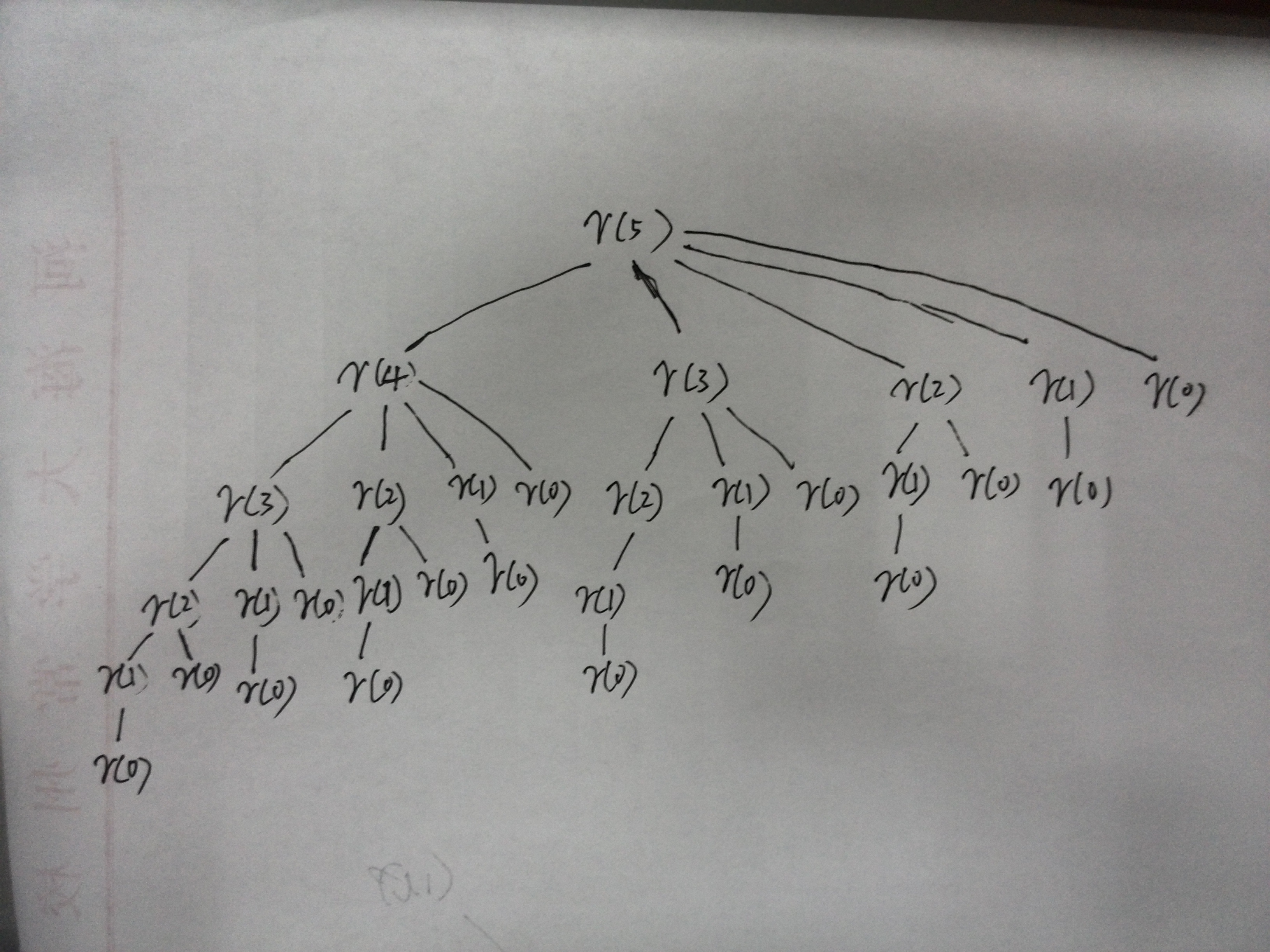
从递归树中可以看出有大量的求解都是重叠的,所以也满足动态规划的第二个特征,那么这个问题选择用动态规划的方法来求解很可能是一个很好的办法!
经过分析已经得出递归最优子结构:r(n)=max{p(1)+r(n-1),p(2)+r(n-2),......p(n-1)+r(1),p(n)+r(0)}
带备忘的自顶向下法伪代码:
1 memoized_cut(p,n) 2 let r[0...n]be a new array 3 for i=0 to n 4 r[i]=-1 5 return memoized_cut_digui(p,n,r) 6 7 8 9 memoized_cut_digui(p,n,r) 10 if(r[n]>=0) 11 return r[n] 12 if(0==n) 13 temp=0
14 else 15 temp=-1 16 for i=1 to n 17 if(p[i]+memoized_cut_digui(p,n-i,r)>temp) 18 temp=p[i]+memoized_cut_digui(p,n-i,r) 19 r[n]=temp 20 return temp 21 22
带备忘的自顶向下法C++程序:
1 #include<iostream> 2 using namespace std; 3 int memoized_cut_digui(int *p,int n,int *r) 4 { 5 int temp; 6 if(r[n]>=0) 7 { 8 return r[n]; 9 } 10 if(n==0) 11 { 12 temp=0; 13 } 14 else temp=-1; 15 for(int i=1;i<=n;i++) 16 { 17 if((p[i]+memoized_cut_digui(p,n-i,r))>temp) 18 { 19 temp=p[i]+memoized_cut_digui(p,n-i,r); 20 } 21 } 22 r[n]=temp; 23 return temp; 24 } 25 int memoized_cut(int *p,int n) 26 { 27 int *r=new int[n]; 28 memset(r,-1,n); //将r数组全部赋值为-1 29 return memoized_cut_digui(p,n,r); 30 } 31 int main() 32 { 33 int p[11]={0,1,5,8,9,10,17,17,20,24,30}; 34 int n; 35 cin>>n; 36 cout<<memoized_cut(p,n); 37 return 0; 38 }
自底向上法伪代码:
1 memoized_cut(p,n) 2 let r[0...n]be a new array 3 r[0]=0 4 for i=1 to n 5 temp=-1 6 for j=1 to i 7 if(p[j]+r[i-j]>temp) 8 temp=p[j]+r[i-j] 9 r[i]=temp 10 return r[n]
自底向上法C++代码
1 #include<iostream> 2 using namespace std; 3 int memoized_cut(int *p,int n) 4 { 5 int *r=new int[n+1]; 6 r[0]=0; 7 //从r[1]逐次求解一直到r[n] 8 for(int i=1;i<=n;i++) 9 { 10 int temp=-1; 11 //求解每一个r[i]的时候都需要将它及它之前的每一段先切第一刀的可能性都遍历一遍,然后求这次遍历中得到的最大值为这个i下的最优解 12 for(int j=1;j<=i;j++) 13 { 14 if(p[j]+r[i-j]>temp) 15 { 16 temp=p[j]+r[i-j]; 17 } 18 19 } 20 r[i]=temp; 21 } 22 return r[n]; 23 } 24 25 int main() 26 { 27 int p[11]={0,1,5,8,9,10,17,17,20,24,30}; 28 int n; 29 cin>>n; 30 cout<<memoized_cut(p,n); 31 return 0; 32 }
重构解
前面只求出了最优的收益值,并没有返回解的本身(没有给出最优的情况下,应该分成每个子段的长度值),为此我们可以在动态规划保存最优解的同时保存切割方案,然后对最优方案进行输出。
伪代码如下:
1 memoized_cut(p,n) 2 let r[0...n]be a new array 3 r[0]=0 4 for i=1 to n 5 temp=-1 6 for j=1 to i 7 if(p[j]+r[i-j]>temp) 8 temp=p[j]+r[i-j] 9 s[i]=j//保存最优解 10 r[i]=temp 11 return r[n] and s 12 13 14 15 16 print_zuiyoujie(s,n) 17 while n>0 18 cout s[n] 19 n=n-s[n]
C++程序如下:
1 #include<iostream> 2 using namespace std; 3 int memoized_cut(int *p,int n,int *s) 4 { 5 int *r=new int[n+1]; 6 r[0]=0; 7 //从r[1]逐次求解一直到r[n] 8 for(int i=1;i<=n;i++) 9 { 10 int temp=-1; 11 //求解每一个r[i]的时候都需要将它及它之前的每一段先切第一刀的可能性都遍历一遍,然后求这次遍历中得到的最大值为这个i下的最优解 12 for(int j=1;j<=i;j++) 13 { 14 if(p[j]+r[i-j]>temp) 15 { 16 temp=p[j]+r[i-j]; 17 *(s+i)=j; 18 } 19 20 } 21 r[i]=temp; 22 } 23 return r[n]; 24 } 25 26 int main() 27 { 28 int p[11]={0,1,5,8,9,10,17,17,20,24,30}; 29 int *s=NULL; 30 s=new int [11]; 31 int n; 32 cin>>n; 33 cout<<"最大的收益为"<<memoized_cut(p,n,s)<<endl; 34 cout<<"最佳切割方案是:"<<endl; 35 while(n) 36 { 37 cout<<s[n]<<endl; 38 n=n-s[n]; 39 } 40 return 0; 41 }