剑指offer13

地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

分析：该题分析是一个矩阵的遍历过程，但是不可以直接使用两个嵌套for循环来遍历，求取满足条件的坐标点个数，因为存在着某些点满足条件，但是其周围的点都是不可达的，那么该点还是不可达。所以判断点是否可达应该一个点一个点的来看，我想到的是使用回溯法的方法，用stack来记录当前的坐标点，栈不为空就pop栈顶坐标，分析该坐标是否可达，之后分别分析将该点下移和右移是否满足条件（为啥只需要下移和右移后面分析,这个问题是我做这题的时候一个很难想的问题），满足则push入栈，否则跳过。其实我觉得也可以使用队列，也是可以的。

问题：为什么只需要看向下移动和向右移动，而不需要看向上移动和向左移动？题目中的数位之和记为f()

若相邻的三个数分别为x-1，x，x+1,一定只会x-1满足条件，其他x，x+1满足不满足均有可能，一定不会x-1不满足，x，x+1满足条件
当x+1不发生十位上的进位时，则f(x-1)<f(x)<f(x+1)，当x-1不满足的时候，x,x+1肯定也不满足
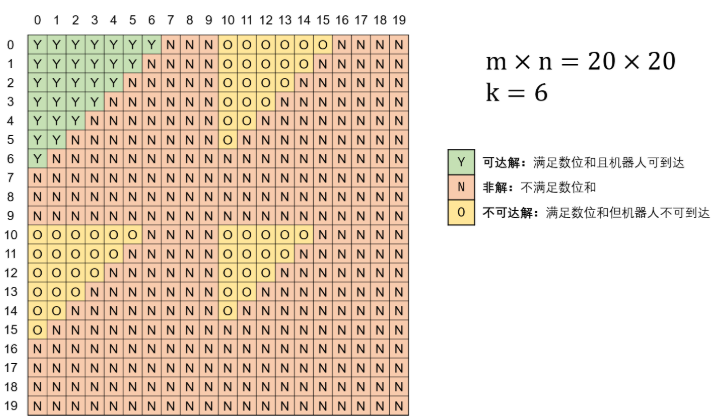
当x+1发生个位上的进位时，f(x+1)+8 = f(x),f(x-1)+1 = f(x)，所以可以发现解的情况应该是如上图所示的，从坐标领零点开始，下面一行的解总是比上一行的少一个，而且第一行的解也会在个位发生进位的时候发生突变，这样原本本来一直不满足的点，经过进位可能就满足了，但是尽管这样解也同样是一个上图的三角形，最好的情况也是第一行的两个三角形连起来，但这样同样只需要向下，向右遍历即可，若两个三角形的解不相连更不用说，我在做这题的时候这个地方困扰了我好久，开始一直想着应该四个方向，但是这样就会发生死循环，经过回过头的分析，以后做题想不通的要学会手动推导一下，不要仅仅画一些简单的示意图。

算法代码：

class Solution {

    public int movingCount(int m,int n,int k){
        // 状态矩阵用来记录某一个点是否已经检测可达，可达标为1，默认为零，不可达为-1
        int[][] state = new int[m][n];
        int num = 0; // 记录可达的数量

        // 定义初始的坐标x,y变量
        int x=0,y=0;
        Stack<int[]> stack = new Stack();
        stack.push(new int[]{x,y});

        while(!stack.empty()){
            int[] temp = stack.pop();
            x = temp[0];y = temp[1];
            // 判断pop出的坐标是否符合,不符合就不用看向前后左右移动
            if(isOk(temp[0],temp[1],k)){
                if(state[x][y] != 1) {num++; state[x][y] = 1;}
                // 向下，如何合规就push
                if(x+1<m&&isOk(x+1,y,k)&&state[x+1][y]==0) stack.push(new int[]{x+1,y});

                // 向右，如果合规就push
                if(y+1<n&&isOk(x,y+1,k)&&state[x][y+1]==0) stack.push(new int[]{x,y+1});
            }
        }

        return num;
    }


    // 判断（x,y）是否是合法的位置
    public static boolean isOk(int x,int y,int k){
        int sum = 0;
        while(x>=10){sum += x%10; x/=10;}
        while(y>=10){sum += y%10; y/=10;}

        return sum+x+y<=k?true:false;
    }
}