BFS

BFS

所谓宽度优先，就是每次都尝试访问同一层的节点。 如果同一层都访问完了，再访问下一层。

这样做的结果是，BFS 算法找到的路径是从起点开始的 最短 合法路径。换言之，这条路所包含的边数最小。

在 BFS 结束时，每个节点都是通过从起点到该点的最短路径访问的。

实现

bfs(s) {
  q = new queue()
  q.push(s), visited[s] = true
  while (!q.empty()) {
    u = q.pop()
    for each edge(u, v) {
      if (!visited[v]) {
        q.push(v)
        visited[v] = true
      }
    }
  }
}

应用场景

• 迷宫图求最短路，求连通性
• 图论
  1. 树的层序遍历
  2. 图的最短路，连通性（求图的联通分量，跑多次BFS，例题：flood fill)
• 隐式图搜索 ，找最短路
  1. 建立显示图
  2. 通过状态转移找点
• 拓扑排序
• 分层图

0-1 BFS（双端队列BFS）

详细教程

 边权值为可能有，也可能没有（由于 BFS 适用于权值为 1 的图，所以一般是 0 or 1），或者能够转化为这种边权值的最短路问题。

一般情况下，我们把没有权值的边扩展到的点放到队首，有权值的边扩展到的点放到队尾。这样即可保证在整个队列中，像普通 BFS 一样，越靠近队首，权值越小，且权值零一之间有分隔。

while (队列不为空) {
  int u = 队首;
  弹出队首;
  if (vis[u]) continue;
  vis[u] = 1;
  for (枚举 u 的邻居) {
    更新数据
    if (...)
      添加到队首;
    else
      添加到队尾;
  }
}

优先队列BFS 

优先队列，相当于一个二叉堆，STL 中提供了 std::priority_queue，可以方便我们使用优先队列。

在基于优先队列的 BFS 中，我们每次从队首取出代价最小的结点进行进一步搜索。容易证明这个贪心思想是正确的，

因为从这个结点开始扩展的搜索，一定不会更新原来那些代价更高的结点。换句话说，其余那些代价更高的结点，我们不回去考虑更新它。

当然，每个结点可能会被入队多次，只是每次入队的代价不同。当该结点第一次从优先队列中取出，以后便无需再在该结点进行搜索，直接忽略即可。

所以，优先队列的 BFS 当中，每个结点只会被处理一次。

相对于普通队列的 BFS，时间复杂度多了一个$log$，毕竟要维护这个优先队列嘛。不过普通 BFS 有可能每个结点入队、出队多次，时间复杂度会达到$O(n^2)$，不是$O(n)$。所以优先队列 BFS 通常还是快的。

诶？这怎么听起来这么像堆优化的 Dijkstra 算法呢？事实上，堆优化 Dijkstra 就是优先队列 BFS。

LC102. Binary Tree Level Order Traversal

层序遍历二叉树，按层输出

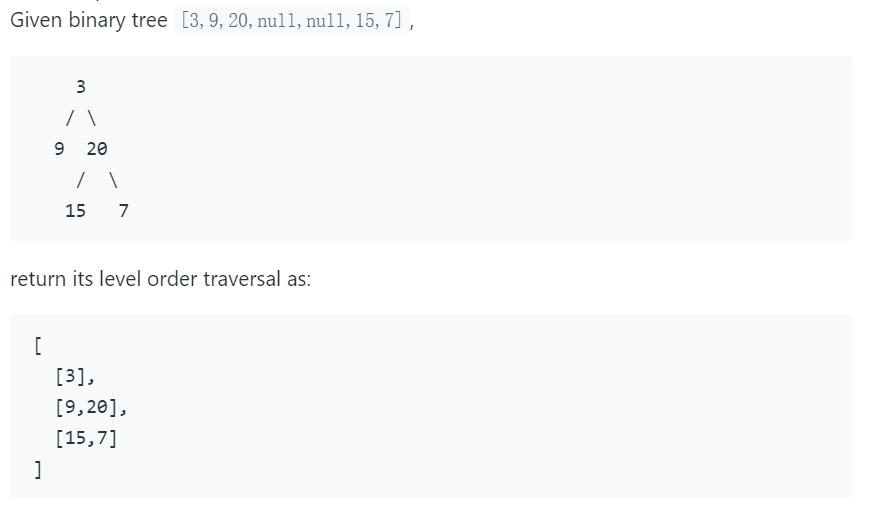
 方法一：BFS

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res;
        if (!root) return res;
        queue<TreeNode*> q;
        q.push(root);
        while (!q.empty()) {
            int levelNum = q.size();
            vector<int> level;
            for (int i = 0; i < levelNum; ++i) {
                TreeNode* t = q.front(); q.pop();
                level.push_back(t->val);
                if (t->left) q.push(t->left);
                if (t->right) q.push(t->right);
            }
            res.push_back(level);
        }
        return res;
    }
};

方法二：DFS

由于是每一层放入一个vector，因此可以用dfs，用一个参数记录深度信息，将当前节点插入对应深度的结果vector中

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> res;
    void dfs(TreeNode* u, int dep) {
        if (!u) return;
        if (res.size() == dep) res.emplace_back();
        res[dep].push_back(u->val);
        dfs(u->left, dep + 1);
        dfs(u->right, dep + 1);
    }
    vector<vector<int>> levelOrder(TreeNode* root) {
        dfs(root, 0);
        return res;
    }
};

本题类似题目

LC429. N-ary Tree Level Order Traversal n叉树层序遍历

LC1091. Shortest Path in Binary Matrix 迷宫图问题，记住此模板

class Solution {
public:
    typedef pair<int, int> PII;
    int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
        int n = grid.size();
        if (grid[0][0] || grid[n - 1][n - 1]) return -1;
        grid[0][0] = 1;
        queue<PII> q;
        q.emplace(0, 0);
        while (!q.empty()) {
            PII u = q.front();
            q.pop();
            int x = u.first, y = u.second;
            for (int i = -1; i <= 1; ++i) {
                for (int j = -1; j <= 1; ++j) {
                    int nx = x + i;
                    int ny = y + j;
                    if (nx < 0 || nx >= n || ny < 0 || ny >= n || grid[nx][ny]) continue;
                    grid[nx][ny] = grid[x][y] + 1;
                    q.emplace(nx, ny);
                }
            }
        }
        return grid[n - 1][n - 1] == 0 ? -1 : grid[n - 1][n - 1];
    }
};

LC279. Perfect Squares

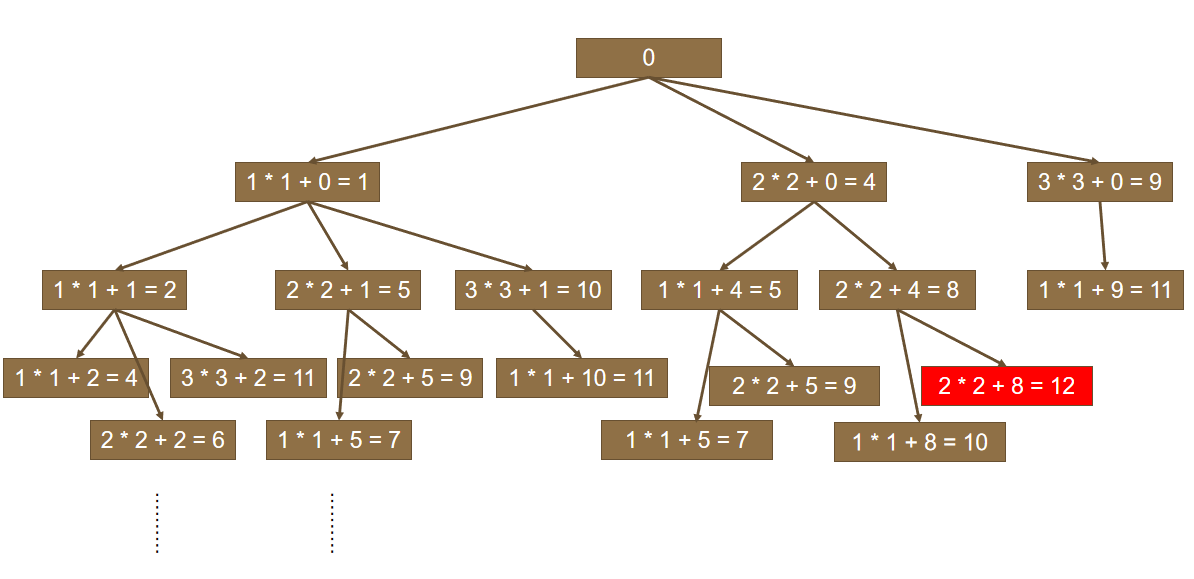
完美平方数为1，4，9，16，···，给定n，求和为n的完美平方数的最小个数。

这道题可以转换为完全背包问题，也可以用BFS做。从节点0开始，下一层能到的数入队，以此类推，直到遇到节点n，结果就是层数。

class Solution {
public:
    int numSquares(int n) {
        queue<int> q;
        unordered_set<int> vis;
        q.push(0);
        vis.insert(0);
        int d = 0;
        while (!q.empty()) {
            d++;
            int size = q.size();
            for (int i = 0; i < size; i++) {
                int f = q.front();
                q.pop();
                for (int j = 1; j * j + f <= n; ++j) {
                    int next = j * j + f;
                    if (next == n) return d;
                    if (!vis.count(next)) {
                        q.push(next);
                        vis.insert(next);
                    }
                }
            }
        }
        return 0;
    }
};

LC1368. Minimum Cost to Make at Least One Valid Path in a Grid

 方法一：Dijkstra算法

Dijkstra算法适合用来求出无负权边图中的单源最短路径。由于所有边的权值均为0或1，并且我们只需要求出从$(0, 0)$到$(m - 1, n - 1)$的最短路，因此可以直接套用Dijkstra算法得到答案。

class Solution {
private:
    static constexpr int dirs[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};

public:
    int minCost(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<int> dist(m * n, INT_MAX);
        vector<int> seen(m * n, 0);
        dist[0] = 0;
        priority_queue<PII, vector<PII>, greater<PII>> q;
        q.emplace(0, 0);
        
        while (!q.empty()) {
            auto [cur_dis, cur_pos] = q.top();
            q.pop();
            if (seen[cur_pos]) {
                continue;
            }
            seen[cur_pos] = 1;
            int x = cur_pos / n;
            int y = cur_pos % n;
            for (int i = 0; i < 4; ++i) {
                int nx = x + dirs[i][0];
                int ny = y + dirs[i][1];
                int new_pos = nx * n + ny;
                int new_dis = cur_dis + (grid[x][y] != i + 1);
                
                if (nx >= 0 && nx < m && ny >= 0 && ny < n && new_dis < dist[new_pos]) {
                    dist[new_pos] = new_dis;
                    q.emplace(new_dis, new_pos);
                }
            }
        }

        return dist[m * n - 1];
    }
};

方法二：0-1 BFS

class Solution {
private:
    static constexpr int dirs[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};

public:
    int minCost(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<int> dist(m * n, INT_MAX);
        vector<int> seen(m * n, 0);
        dist[0] = 0;
        deque<int> q;
        q.push_back(0);
        
        while (!q.empty()) {
            auto cur_pos = q.front();
            q.pop_front();
            if (seen[cur_pos]) {
                continue;
            }
            seen[cur_pos] = 1;
            int x = cur_pos / n;
            int y = cur_pos % n;
            for (int i = 0; i < 4; ++i) {
                int nx = x + dirs[i][0];
                int ny = y + dirs[i][1];
                int new_pos = nx * n + ny;
                int new_dis = dist[cur_pos] + (grid[x][y] != i + 1);
                
                if (nx >= 0 && nx < m && ny >= 0 && ny < n && new_dis < dist[new_pos]) {
                    dist[new_pos] = new_dis;
                    if (grid[x][y] == i + 1) {
                        q.push_front(new_pos);
                    }
                    else {
                        q.push_back(new_pos);
                    }
                }
            }
        }

        return dist[m * n - 1];
    }
};

 

LC407. Trapping Rain Water II

$m imes n$矩阵代表二维高度图中每个单元的高度，计算图中形状最多能接多少体积的雨水。

解法：优先队列BFS

class Solution {
public:
    int trapRainWater(vector<vector<int>>& heightMap) {
        if (heightMap.size() == 0) return 0;
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>>q;
        int row = heightMap.size(), col = heightMap[0].size();
        vector<vector<int>> visited(row, vector<int>(col, 0));
        int ans = 0, Max = INT_MIN;
        for (int i = 0; i < row; ++i) {
            for (int j = 0; j < col; ++j) {
                if (!(i == 0 || i == row - 1 || j == 0 || j == col - 1)) continue;
                q.emplace(heightMap[i][j], i * col + j);
                visited[i][j] = 1;
            }
        }
        vector<vector<int>> dir{{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
        while (!q.empty()) {
            auto val = q.top();
            q.pop();
            int height = val.first, x = val.second / col, y = val.second % col;
            Max = max(Max, height);
            for (auto& d : dir) {
                int x2 = x + d[0], y2 = y + d[1];
                if (x2 >= row || x2 < 0 || y2 >= col || y2 < 0 || visited[x2][y2]) continue;
                visited[x2][y2] = 1;
                if (heightMap[x2][y2] < Max) ans += Max - heightMap[x2][y2];
                q.emplace(heightMap[x2][y2], x2 * col + y2);
            }
        }
        return ans;
    }
};

 LC301. Remove Invalid Parentheses

一个字符串，包含括号和字母，删除最少的括号，使字符串合法，输出所有可能的结果。

分析：用BFS，初始点为原字符串，第一层，从原字符串删去任意一个括号，将所有可能结果加入队列，判断该层是否有有效字符串，如果有，找到所有有效字符串即可，如果没有，取出队首字符串，开始第二层遍历。

class Solution {
public:
    vector<string> removeInvalidParentheses(string s) {
        vector<string> res;
        if(s.empty()) return {""};
        unordered_set<string> vis;
        queue<string> q;
        q.push(s);
        vis.insert(s);
        bool found = false;
        while (!q.empty()) {
            auto  f = q.front();
            q.pop();
            if (isValid(f)) {
                res.push_back(f);
                found = true;
            }
            if (found) continue;
            for (int i = 0; i < f.size(); ++i) {
                if (f[i] != '(' && f[i] != ')') continue;
                string t = f.substr(0, i) + f.substr(i + 1);
                if (!vis.count(t)) {
                    q.push(t);
                    vis.insert(t);
                }
            }
        }
        return res;
    }
    
    bool isValid(string& s) {
        int cnt = 0; 
        for (char& c : s) {
            if (c == '(') cnt++;
            if (c == ')' && cnt-- == 0) return false;
        }
        return cnt == 0;
    }
};