There is an m by n grid with a ball. Given the start coordinate (i,j) of the ball, you can move the ball to adjacent cell or cross the grid boundary in four directions (up, down, left, right). However, you can at most move N times. Find out the number of paths to move the ball out of grid boundary. The answer may be very large, return it after mod 109 + 7.
Example 1:
Input:m = 2, n = 2, N = 2, i = 0, j = 0
Output: 6
Explanation:
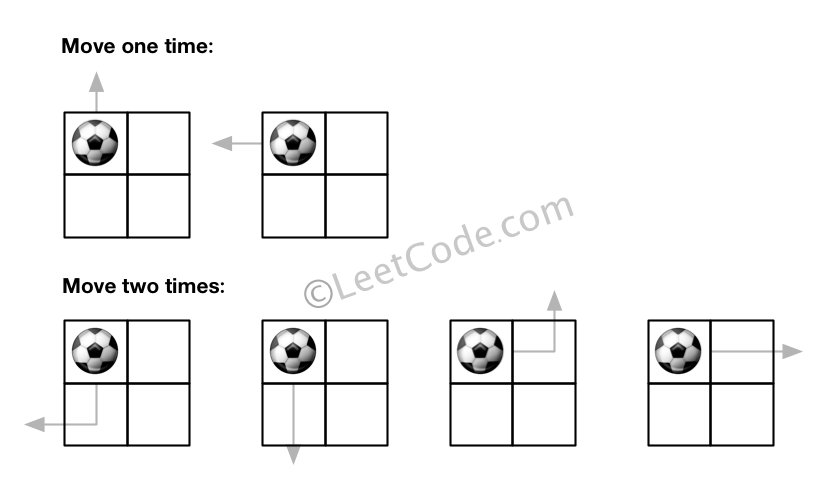
Example 2:
Input:m = 1, n = 3, N = 3, i = 0, j = 1
Output: 12
Explanation:
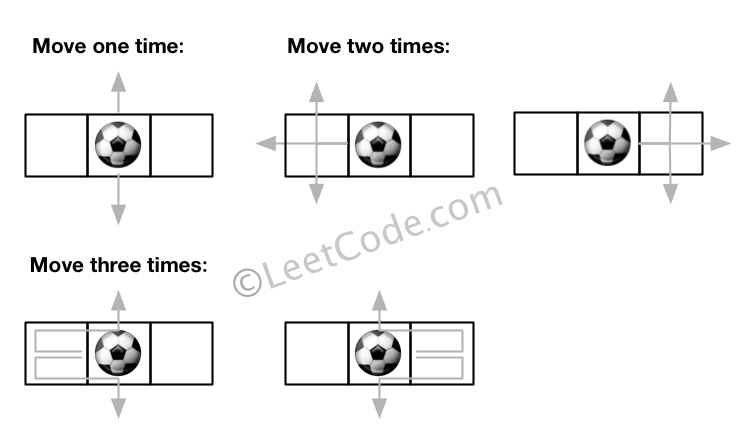
Note:
- Once you move the ball out of boundary, you cannot move it back.
- The length and height of the grid is in range [1,50].
- N is in range [0,50].
Solution1:(TLE)
class Solution:
def findPaths(self, m, n, N, i, j):
"""
:type m: int
:type n: int
:type N: int
:type i: int
:type j: int
:rtype: int
"""
if i==-1 or j==-1 or i==m or j==n:
return 1
if N==0:
return 0
return self.findPaths(m,n,N-1,i-1,j) + self.findPaths(m,n,N-1,i+1,j) + self.findPaths(m,n,N-1,i,j+1) + self.findPaths(m,n,N-1,i,j-1)
Solution2:
class Solution:
def findPaths(self, m, n, N, i, j):
"""
:type m: int
:type n: int
:type N: int
:type i: int
:type j: int
:rtype: int
"""
if N==0:
return 0
MOD = 1000000000 + 7
res = 0
dp = [[[0 for p in range(N+1)]for q in range(n) ]for t in range(m)]
for t in range(1,N+1):
for p in range(m):
for q in range(n):
left = 1 if p==0 else dp[p-1][q][t-1]
right = 1 if p==m-1 else dp[p+1][q][t-1]
up = 1 if q==0 else dp[p][q-1][t-1]
down = 1 if q==n-1 else dp[p][q+1][t-1]
dp[p][q][t] = (left + right + up + down)%MOD
return dp[i][j][N]
对于一个起始点为i,j,N步可以走出的点的路径个数,等于该点周围的4个点,N-1步可以走出的路径个数之和,知道了这个之后,我们就可以以这个公式作为状态转移方程。