二分查找法在算法家族大类中属于“分治法”,二分查找的过程比较简单,代码见我的另一篇日志,戳这里!因二分查找所涉及的有序表是一个向量,若有插入和删除结点的操作,则维护表的有序性所花的代价是O(n)。
就查找性能而言,二叉查找树和二分查找不分伯仲,但是,就维护表的有序性而言,二叉排序树无须移动结点,只需修改指针即可完成插入和删除操作,且其平均的执行时间均为O(lgn),因此更有效。二叉查找树,顾名思义,是一种可以用来二分查找的树数据结构,其左孩子比父节点小,右孩子比父节点大,还有一个特性就是”中序遍历“可以让结点有序。在对关键字进行查找的时候,根据关键字与根节点的关键字比较的结果,分别选择继续与其左子树或者右子树进行比较,直到找到所查找的关键字或者访问节点的左右子树不存在(没找到关键字)则退出!
二叉查找树的主要操作有:插入关键字,查找关键字,删除关键字。下面分别对这三个步骤做详细描述和算法实现。
为了方便,我将二叉查找树实现为一个类,结构如下:
typedef struct Node_ { struct Node_ *parent; struct Node_ *left; struct Node_ *right; T data; }Node; class BinaryTree { public: BinaryTree():root(NULL){}; ~BinaryTree(); bool insertNode(T data); bool deleteNode(T data); Node* findNode(T data); private: Node *root; };
1. 插入关键字的过程如下所示:
插入过程的代码如下:
bool BinaryTree::insertNode(T data) { Node *x = NULL, *current, *parent; /*********************************************** * allocate node for data and insert in tree * ***********************************************/ /* find x's parent */ current = root; parent = NULL; while (current) { if (compEQ(data, current->data)) return true; parent = current; current = compLT(data, current->data) ? current->left : current->right; } /* setup new node */ if ((x = (Node*)malloc(sizeof(*x))) == 0) { cout << "Insufficient memory (insertNode)!" << endl; return false; } x->data = data; x->parent = parent; x->left = NULL; x->right = NULL; /* insert x in tree*/ if(parent) if(compLT(x->data, parent->data)) parent->left = x; else parent->right = x; else root = x; return true; }
其中的compEQ和compLT为2个宏定义,用来比较两个关键字的大小。
2. 查找关键字的过程比较简单,和二分查找方法类似,代码如下:
Node* BinaryTree::findNode(T data) { /******************************* * find node containing data * *******************************/ Node *current = root; while(current != NULL) if(compEQ(data, current->data)) return current; else current = compLT(data, current->data) ? current->left : current->right; return NULL; }
3. 删除关键字的过程分为2种情况讨论:单孩子的情况和左右孩子的情况。
1> 单孩子情况分析:
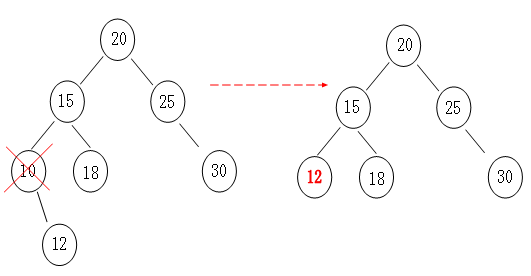
如果删除的节点有左孩子那就把左孩子顶上去,如果有右孩子就把右孩子顶上去,so easy!如图所示:
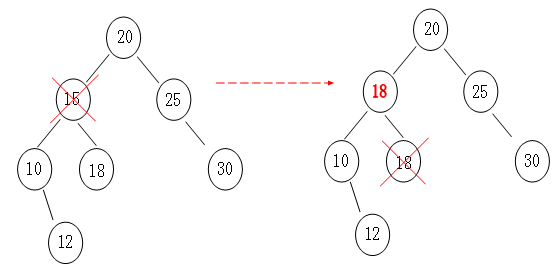
2> 左右孩子情况分析:
首先可以这么想象,如果我们要删除一个数组的元素,那么我们在删除后会将其后面的一个元素顶到被删除的位置,如下图所示:
那么二叉树操作同样也是一样,我们根据“中序遍历(inorder tree walk)”找到要删除结点的后一个结点,然后顶上去就行了,原理跟“数组”一样一样的。
好了,贴代码:
bool BinaryTree::deleteNode(T data) { Node* pNode = findNode(data); if (pNode == NULL) { cout << "Cannot find this data in BST!" << endl; return false; } Node *x, *y; /* find tree successor */ if (pNode->left == NULL || pNode->right == NULL) y = pNode; else { y = pNode->right; while (y->left != NULL) y = y->left; } /* x is y's only child */ if (y->left != NULL) x = y->left; else x = y->right; /* remove y from the parent chain */ if (x) x->parent = y->parent; if (y->parent) if (y == y->parent->left) y->parent->left = x; else y->parent->right = x; else root = x; /* y is the node we're removing */ /* z is the data we're removing */ /* if z and y are not the same, replace z with y. */ if (y != pNode) { y->left = pNode->left; if (y->left) y->left->parent = y; y->right = pNode->right; if (y->right) y->right->parent = y; y->parent = pNode->parent; if (pNode->parent) if (pNode == pNode->parent->left) pNode->parent->left = y; else pNode->parent->right = y; else root = y; free (pNode); } else { free (y); } return true; }
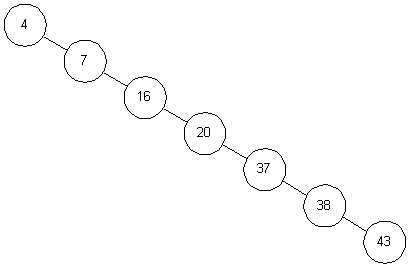
好了,二叉查找树的代码告一段落,我们在来分析一下二叉查找树的插入过程,假如有以下序列:<4, 17, 16, 20, 37, 38, 43>,则会生成如下所示二叉树:
这已经完全退化成了一个单链表,势必影响到关键字的查找过程。不过总会有解决办法的,下一篇博客我将继续这个话题,对普通二叉树经过旋转,即使用平衡二叉树,使其保持最坏复杂度在O(logN)。
谢谢大家的阅读,希望能够帮到大家!PS:文章中部分图片利用了博客园另外一篇文章的插图(戳这里)!
Published by Windows Live Write!