Tarjan求LCA（离线）

基本思想

把要求的点对保存下来，在dfs时顺带求出来。

方法

将每个已经遍历的点指向它回溯的最高节点(遍历它的子树时指向自己),
每遍历到一个点就处理它存在的询问
如果另一个点已经遍历,则lca就是另一个点指向的点。否则跳过

例如在下图中询问4,5和4,3的lca，遍历顺序为1,2,4,5,3

遍历到4时,各个点的指向如图

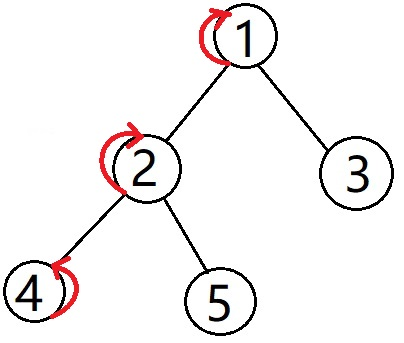
处理询问4,5和4,3。发现3和5没有遍历,跳过

回溯到3，然后遍历5。

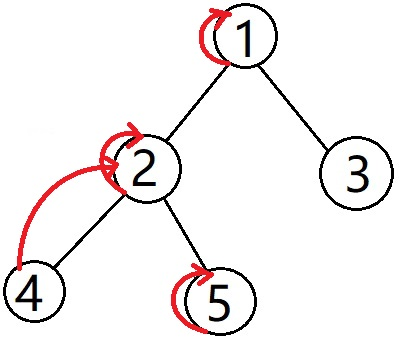
发现4遍历过了，4,5的lca为2

然后回溯到1，遍历3

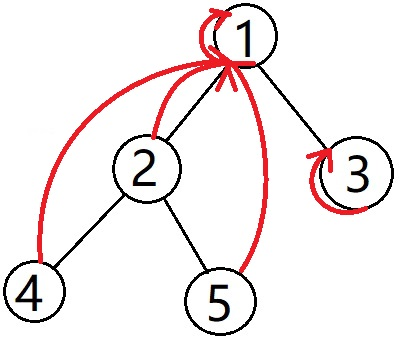
发现4遍历过了，4,3的lca为1

具体每个点的指向可以用并查集实现,每个询问可以用邻接表存储

具体实现

 P3379 【模板】最近公共祖先（LCA）

#include<cstdio>
#define maxn 500005
struct Edge{
    int next,to;
}edge[maxn*2],q[maxn*2];
int n,m,fi[maxn],se,qi[maxn],sq=1,find[maxn],lca[maxn];
bool vis[maxn];
inline void add_edge(int u,int v){
    edge[++se].next=fi[u],edge[se].to=v,fi[u]=se,
    edge[++se].next=fi[v],edge[se].to=u,fi[v]=se;
}
inline void add_q(int u,int v){
    q[++sq].next=qi[u],q[sq].to=v,qi[u]=sq,
    q[++sq].next=qi[v],q[sq].to=u,qi[v]=sq;
}
int search(int x){//查找x指向的节点 
    if(find[x]==x)return x;
    return find[x]=search(find[x]);
}
void Tarjan(int x,int f){//Tarjan求LCA 
    find[x]=x,vis[x]=1;//当前节点已经遍历，并指向自己 
    for(int i=fi[x];i;i=edge[i].next){
        int v=edge[i].to;
        if(v==f)continue;
        Tarjan(v,x);
    }
    for(int i=qi[x];i;i=q[i].next){
        int v=q[i].to;
        if(vis[v])lca[i>>1]=search(v);//如果询问的另一个点已经遍历过,则LCA=search(v) 
    }
    find[x]=f;//当前节点及子树指向父亲 
}
int main(){
    int u,v,s;
    scanf("%d%d%d",&n,&m,&s);
    for(int i=1;i<n;i++){
        scanf("%d%d",&u,&v);
        add_edge(u,v);
    }
    for(int i=0;i<m;i++){
        scanf("%d%d",&u,&v);
        add_q(u,v);//将询问用邻接表存储 
    }
    Tarjan(s,0); 
    for(int i=1;i<=m;i++)printf("%d
",lca[i]);
    return 0;
}