一,概念
1,定义:树状数组是一种修改和查询的复杂度都为log(n)的数据结构。
2,应用:可以用来查询任意两位之间的所有元素的和,但是只能修改一个元素的值。
3,应用拓展:可以在简单的修改下,可以以log(n)的复杂度去修改一定范围内的值,但是此时只能查询一个元素的值
4,横向比较:与线段树相比,树状数组可以解决的问题,线段树都可以解决;但是线段树可以解决的问题,树状数组不一定能够解决。
但是相较而言,树状数组效率较高。
二,基本实现与应用代码框架。
图片自己去百度,怎么上传这么慢...
1,树状数组来进行求和。
其对应的很重要的公式,看了图片你就明白有一个A[i],有一个C[i]。
那么出来个公式C[i]=A[i-2^k+1]+A[i-2^k+2]....A[i]。
①k为i对应的二进制下末尾连续零的个数
②A[i-2^k+n]里面的序号数i-2^k+n若大于i,则直接退出。
既然我们要求和
那么还有求和公式
sum[i]=C[i]+C[i-2^k1]+C[i-2^k1-2^k2]....
①同理C[n]里面的值要大于0;
如sum[7]=c[7]+c[6]+c[4]...(里面再往下减就小于0也就没有意义了)
至于比较重要的2^k值怎么算,肯定不可能让你手算555555
记点口诀吧
羽一火一,
int qiuk(int k)
{
return x&(x^(x-1));
}
或者
羽反(逆)
int qiuk(int x)
{
return x&(-x);
}
呵呵,写这么一长串,至于C[n]怎么算,自己看看呗。
appendix:《关于lowbit的实现原理》(即return x&(-x)怎么出来的)
这里利用的负数的存储特性,负数是以补码存储的,对于整数运算 x&(-x)有
● 当x为0时,即 0 & 0,结果为0;
●当x为奇数时,最后一个比特位为1,取反加1没有进位,故x和-x除最后一位外前面的位正好相反,按位与结果为0。结果为1。
●当x为偶数,且为2的m次方时,x的二进制表示中只有一位是1(从右往左的第m+1位),其右边有m位0,故x取反加1后,从右到左第有m个0,第m+1位及其左边全是1。这样,x& (-x) 得到的就是x。
●当x为偶数,却不为2的m次方的形式时,可以写作x= y * (2^k)。其中,y的最低位为1。实际上就是把x用一个奇数左移k位来表示。这时,x的二进制表示最右边有k个0,从右往左第k+1位为1。当对x取反时,最右边的k位0变成1,第k+1位变为0;再加1,最右边的k位就又变成了0,第k+1位因为进位的关系变成了1。左边的位因为没有进位,正好和x原来对应的位上的值相反。二者按位与,得到:第k+1位上为1,左边右边都为0。结果为2^k。
总结一下:x&(-x),当x为0时结果为0;x为奇数时,结果为1;x为偶数时,结果为x中2的最大次方的因子。
反正我没看~
这个东西有专门的称呼lowbit.
其实吧,我来给你总结一下,树状数组的核心的几个东西
①C[i]=A[i-2^k+1]+A[i-2^k+2].....A[i];这个可以记忆成
②sum[i]=C[i-2^k1]+C[i-2^k1-2^k2].....(while(i>0)
③A[i]涉及到,C[i],C[i+2^k],C[(i+2^k)+2^k]....
下图可完美展示这三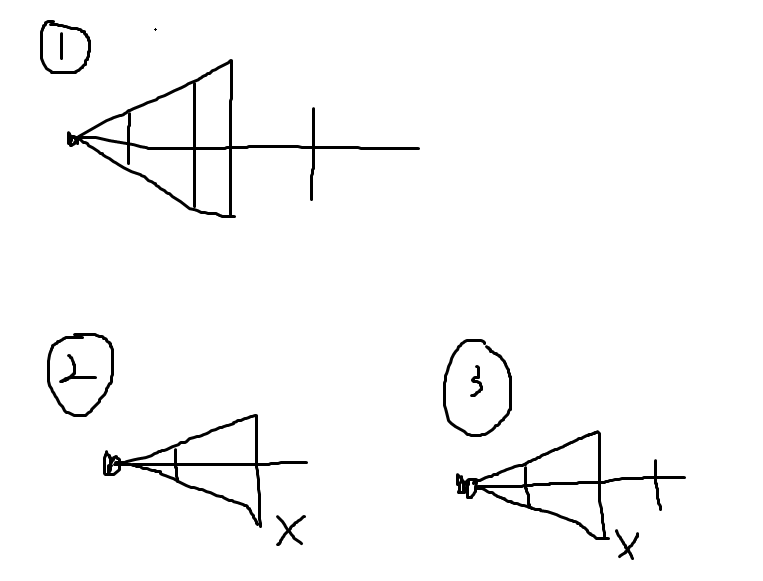 个公式
个公式
模板
1 int n; 2 int A[100000005];//原数组 3 int C[100000005];//树状数组 4 int lowbit(int x) 5 { 6 return x&(-x);//return x&(x^(x-1));这个也行 7 } 8 int update(int i,int x)//在i位置上加上k 9 { 10 //i是位置,x是该位置的值为 11 while(i>=0&&i<=n) 12 { 13 C[i]+=x; 14 i+=lowbit(i); 15 } 16 } 17 int getsum(int i)//求前i项的和 18 { 19 int sum=0; 20 while(i>0) 21 { 22 sum+=C[i]; 23 i-=lowbit(i);//竟然出错了,看来还是要应用一下似乎 24 } 25 return sum; 26 }