决策树是机器学习的常见算法,分为分类树和回归树。当对一个样本的分类进行预测时使用分类树,当对样本的某一个值进行预测时使用回归树。本文是有关决策树的第一部分,主要介绍分类树的几种构建方法,以及如何使用分类树测试分类。
目录如下:
1、分类树的基本概念
2、采用数据集说明
3、划分数据集的几种方式
4、构造分类树
5、使用分类树测试分类
6、写在后面的话
一 分类树的基本概念
分类树(classification tree)简单地说,就是根据训练数据集构造一个类似树形的分类决策模型,然后用这个模型来辅助决策。
例如下图是一个简单的是否举行某个活动的决策树(分类树):
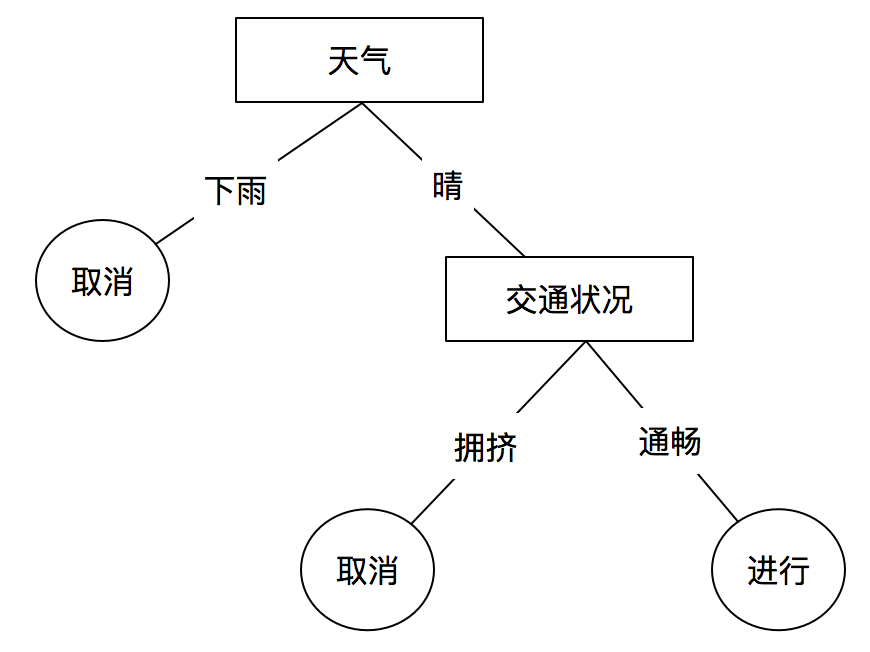
我们可以通过上面的决策树进行预测,当天气晴朗,交通畅通时,我们预测该活动很可能要举办;当天下小雨交通拥挤时,我们预测活动很可能被取消。
这只是一个简单的小例子,真实中的决策树方法包括以下几个步骤:
(1) 收集数据:可以使用任何方法。
(2)准备数据:树构造算法只适用于标称型数据,因此数值型数据必须离散化。
(3)选取划分算法:根据数据的特点,选取合适的划分算法
(4)构造决策树:使用选取的划分算法构造树形的决策模型
(5)测试算法:使用经验树计算错误率
(6)使用算法:使用决策树模型预测决策
二 采用数据集说明
UCI数据集 是机器学习不错的数据集网站,本文选取其中的 Balloons 数据集,将其内容用中文表示如下。
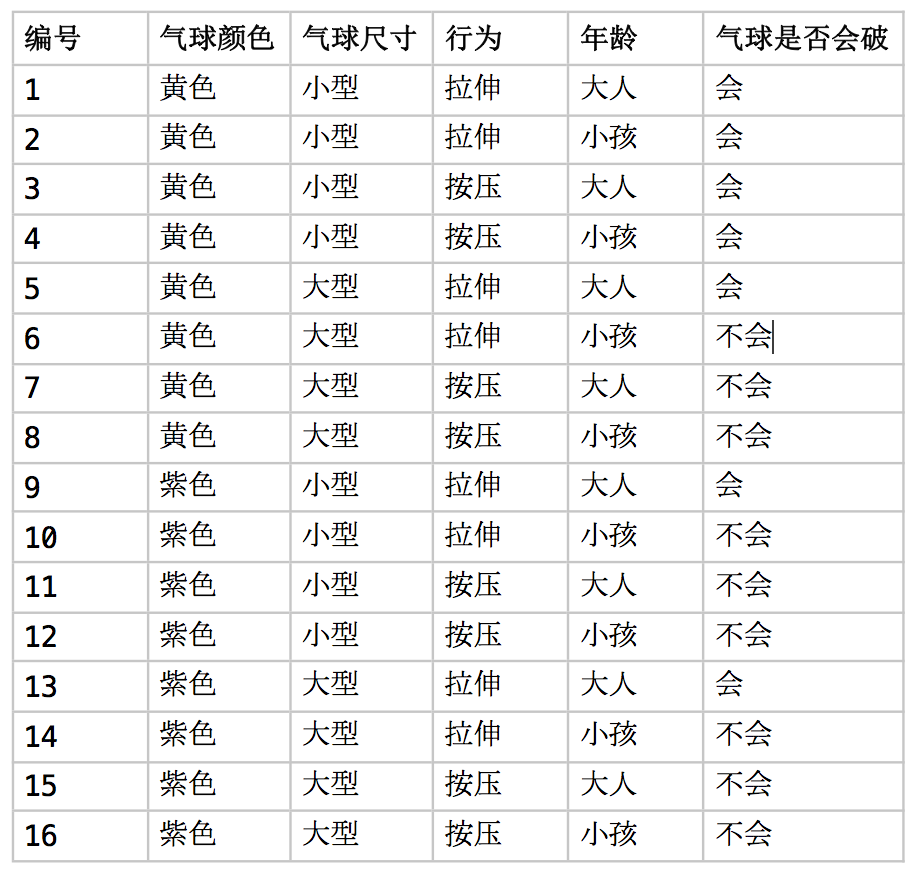
该数据主要是根据几个因素预测气球是否会破。
三 划分数据集的几种方式
决策树的几种经典实现方式是ID3,C4.5 和 CART
其中C4.5是对ID3的改进,C4.5和ID3都是分类树,CART 即可用作分类树,又可用于回归树,当CART用作分类时使用基尼指数作为划分依据,当CART用作回归时使用最小方差作为划分依据。
信息熵
熵(entropy),也即信息熵,是度量样本集合纯度的一种指标。一个数据集的熵越大,则说明该数据分类的纯度越纯。
D表示数据集,假设D共有m个类别,Pk 表示第k个类别占样本总数的比例,数据集熵的公式如下:
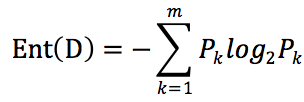
如上面给出的关于气球的数据集,只有 “会” 和 “不会”两种分类,“会”有7个,“不会”有9个,占比分别是 P1 =7/16 , P2=9/16
按照熵的公式 可得 Ent(D) = -P1 * log2P1 - P2*log2P2 = 0.989
代码实现:
1 from math import log 2 import operator 3 4 def calc_entropy(data_set): 5 """计算数据集的熵""" 6 count = len(data_set) 7 label_counts = {} 8 9 # 统计数据集中每种分类的个数 10 for row in data_set: 11 label = row[-1] 12 if label not in label_counts.keys(): 13 label_counts[label] = 1 14 else: 15 label_counts[label] += 1 16 17 # 计算熵 18 entropy = 0.0 19 for key in label_counts: 20 prob = float(label_counts[key]) / count 21 entropy -= prob * log(prob, 2) 22 return entropy
信息增益法
ID3算法使用信息增益作为划分数据集的依据。整个数据集的熵称作 原始熵,数据集D根据某个特征划分之后的熵为条件熵,信息增益 = 原始熵 - 条件熵 。用信息增益划分的具体做法是:计算每一类特征V对应的信息增益,然后挑选信息增益最小的特征进行划分。
信息增益公式为:
![]()
其中v 为特征a的一个分类,pv 为 v分类占特征a总个数的比例,Dv 根据特征a 的v分类进行划分之后的数据集。
代码实现:
1 def choose_best_feature_1(data_set): 2 """选取信息增益最高的特征""" 3 feature_count = len(data_set[0]) - 1 4 # 数据集的原始熵 5 base_entropy = calc_entropy(data_set) 6 # 最大的信息增益 7 best_gain = 0.0 8 # 信息增益最大的特征 9 best_feature = -1 10 11 # 遍历计算每个特征 12 for i in range(feature_count): 13 feature = [example[i] for example in data_set] 14 feature_value_set = set(feature) 15 new_entropy = 0.0 16 17 # 计算信息增益 18 for value in feature_value_set: 19 sub_data_set = split_data_set(data_set, i, value) 20 prob = len(sub_data_set) / float(len(data_set)) 21 new_entropy += prob * calc_entropy(sub_data_set) 22 gain = base_entropy - new_entropy 23 24 # 比较得出最大的信息增益 25 if gain > best_gain: 26 best_gain = gain 27 best_feature = i 28 29 return best_feature
增益率法
ID3所采用的信息增益划分数据集是可能对数目较多的属性有偏好,C4.5 算法避免了这个问题,使用“增益率”来选择最优化分属性。
信息增益率公式:
![]()
其中Gain_ratio(D,a) 表示 根据特征 a 划分之后的信息增益率, IV(a)为 特征a 的固有值
代码实现:
1 def choose_best_feature_2(data_set): 2 """根据增益率选取划分特征""" 3 feature_count = len(data_set[0]) - 1 4 # 数据集的原始熵 5 base_entropy = calc_entropy(data_set) 6 # 最大的信息增益率 7 best_gain_ratio = 0.0 8 # 信息增益率最大的特征 9 best_feature = -1 10 11 # 遍历计算每个特征 12 for i in range(feature_count): 13 feature = [example[i] for example in data_set] 14 feature_value_set = set(feature) 15 new_entropy = 0.0 16 # 固有值 17 intrinsic_value = 0.0 18 19 # 计算信息增益 20 for value in feature_value_set: 21 sub_data_set = split_data_set(data_set, i, value) 22 prob = len(sub_data_set) / float(len(data_set)) 23 new_entropy += prob * calc_entropy(sub_data_set) 24 intrinsic_value -= prob * log(prob, 2) 25 gain = base_entropy - new_entropy 26 gain_ratio = gain / intrinsic_value 27 28 # 比较得出最大的信息增益率 29 if gain_ratio > best_gain_ratio: 30 best_gain_ratio = gain_ratio 31 best_feature = i 32 33 return best_feature
基尼指数法
当CART用做分类树时,使用“基尼指数”来选择划分特征。基尼指数是另外一种表示数据集纯度的指标。
基尼值:
![]()
基尼指数:
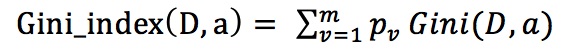
代码实现:
1 def calc_gini(data_set): 2 """计算数据集的基尼值""" 3 count = len(data_set) 4 label_counts = {} 5 6 # 统计数据集中每种分类的个数 7 for row in data_set: 8 label = row[-1] 9 if label not in label_counts.keys(): 10 label_counts[label] = 1 11 else: 12 label_counts[label] += 1 13 14 # 计算基尼值 15 gini = 1.0 16 for key in label_counts: 17 prob = float(label_counts[key]) / count 18 gini -= prob * prob 19 return gini 20 21 22 def choose_best_feature_3(data_set): 23 """根据基尼指数选择划分特征""" 24 feature_count = len(data_set[0]) - 1 25 # 最小基尼指数 26 min_gini_index = 0.0 27 # 基尼指数最小的特征 28 best_feature = -1 29 30 # 遍历计算每个特征 31 for i in range(feature_count): 32 feature = [example[i] for example in data_set] 33 feature_value_set = set(feature) 34 35 # 基尼指数 36 gini_index = 0.0 37 # 计算基尼指数 38 for value in feature_value_set: 39 sub_data_set = split_data_set(data_set, i, value) 40 prob = len(sub_data_set) / float(len(data_set)) 41 gini_index += prob * calc_gini(sub_data_set) 42 43 # 比较得出最小的基尼指数 44 if gini_index < min_gini_index or min_gini_index == 0.0: 45 min_gini_index = gini_index 46 best_feature = i 47 48 return best_feature
四 构造分类树
每次根据划分算法选出最佳的划分特征进行划分,然后对子数据集进行递归划分,直到所有子集的纯度都为1,即构成了决策树。
构造决策树代码:
1 def create_division_tree(data_set, labels): 2 """创建决策树""" 3 class_list = [example[-1] for example in data_set] 4 5 # 所有分类相同时返回 6 if class_list.count(class_list[0]) == len(class_list): 7 return class_list[0] 8 9 # 已经遍历完所有特征 10 if len(data_set[0]) == 1: 11 return get_top_class(class_list) 12 13 # 选取最好的特征 14 best_feat = choose_best_feature_1(data_set) 15 best_feat_label = labels[best_feat] 16 17 # 划分 18 my_tree = {best_feat_label: {}} 19 del (labels[best_feat]) 20 value_set = set([example[best_feat] for example in data_set]) 21 for value in value_set: 22 sub_labels = labels[:] 23 my_tree[best_feat_label][value] = create_division_tree(split_data_set(data_set, best_feat, value), sub_labels) 24 return my_tree
构造的决策树存在在Python 字典类型中,不能直观地看清决策树层次,这里我们使用Matplotlib 模块提供的绘图工具绘制出决策树的模型如下:
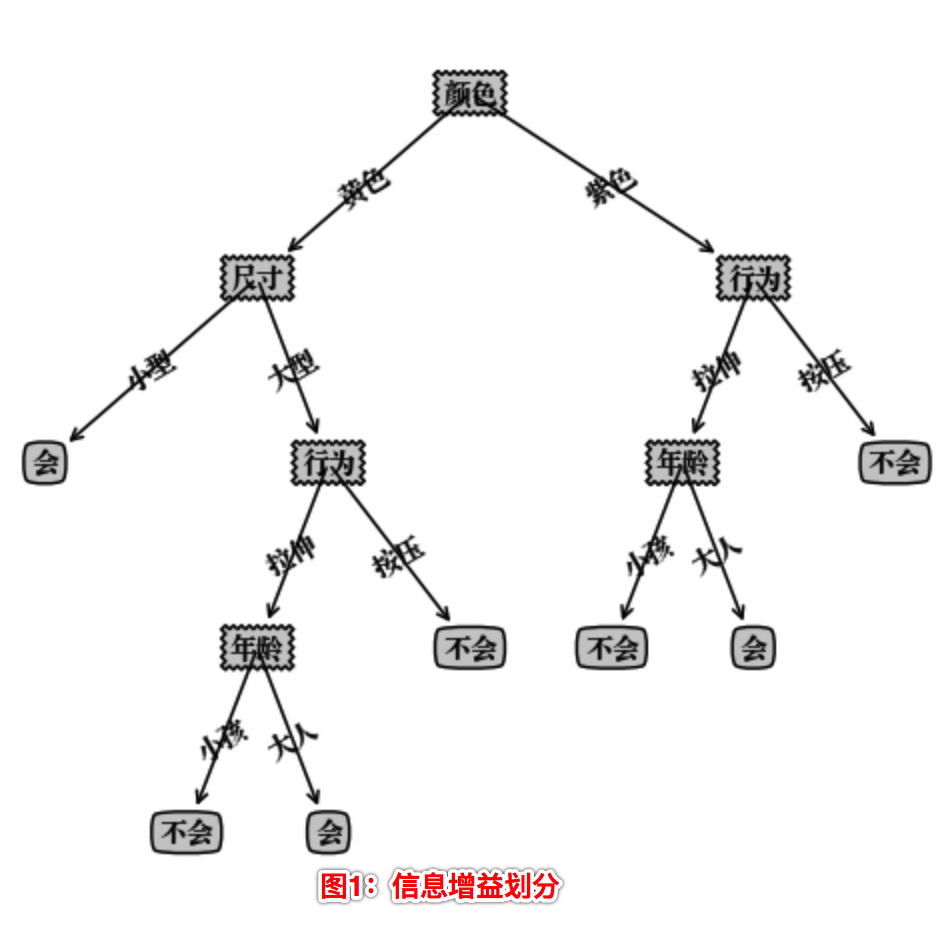
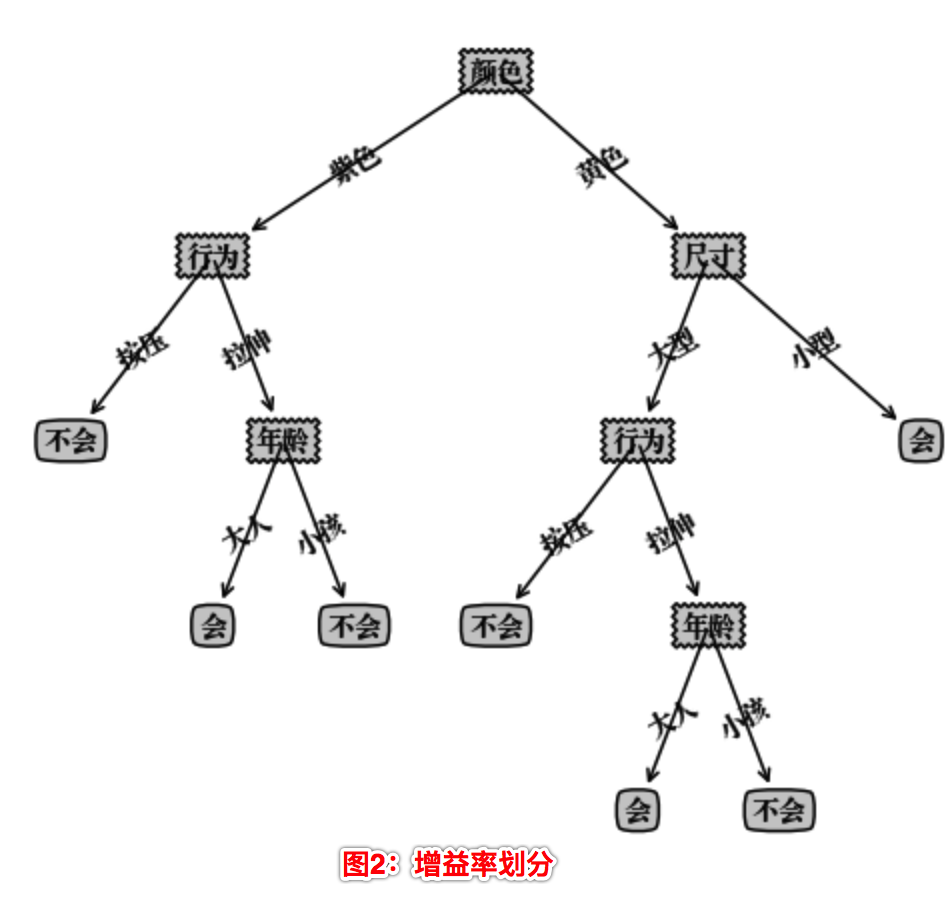
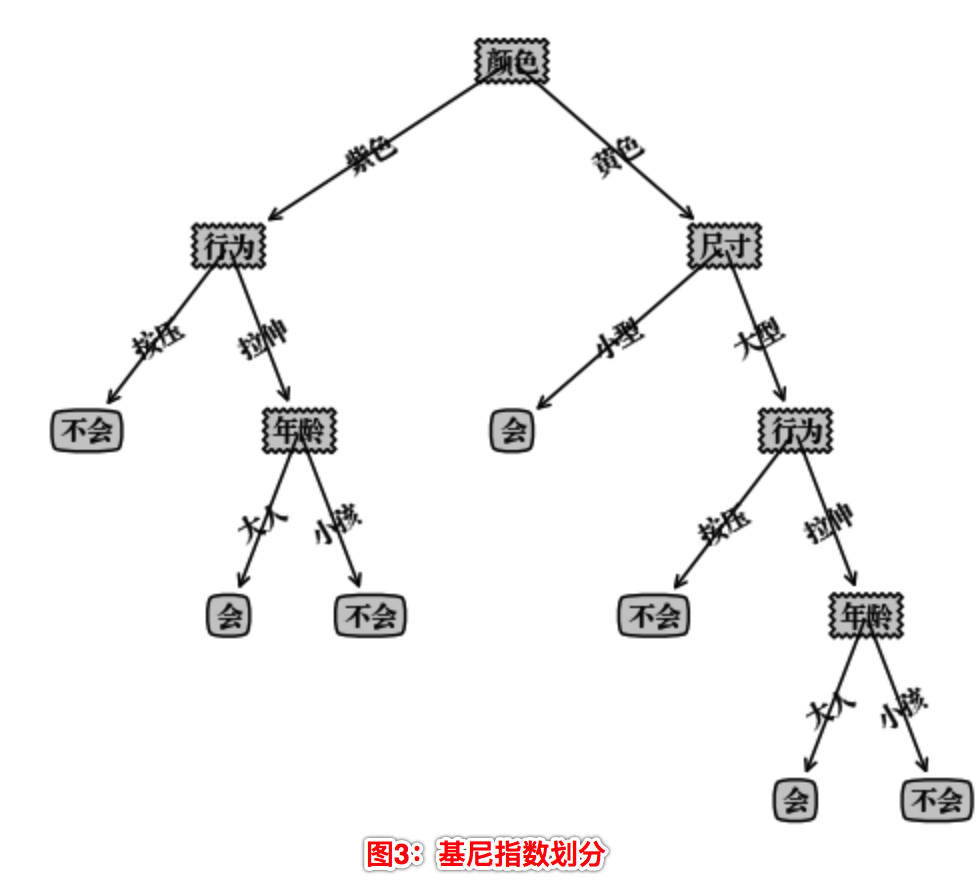
我们可以看到使用不同的划分算法,构造的决策树是不一样的。
五 使用决策树测试分类
通过决策树预测测试样本时,就是根据测试样本的特征属性 从决策树根节点开始不断向下遍历,直到叶子节点。
1 def classify(division_tree, feat_labels, test_vector): 2 """遍历决策树对测试数据进行分类""" 3 first_key = list(division_tree.keys())[0] 4 second_dict = division_tree[first_key] 5 6 feat_index = feat_labels.index(first_key) 7 test_key = test_vector[feat_index] 8 9 test_value = second_dict[test_key] 10 11 if isinstance(test_value, dict): 12 class_label = classify(test_value, feat_labels, test_vector) 13 else: 14 class_label = test_value 15 return class_label
六 写在后面的话
本文完整代码见https://gitee.com/beiyan/machine_learning/tree/master/decision_tree,本文只是分类树方法的简单实现,关于回归树的介绍,以及决策树的剪枝算法,数值型数据离散方法等 将在后序文章中介绍。