排序算法
Mysql中当order by不能使用索引进行排序时,将使用排序算法进行排序:
- 若排序内容能全部放入内存,则仅在内存中使用快速排序;
- 若排序内容不能全部放入内存,则分批次将排好序的内容放入文件,然后将多个文件进行归并排序
- 若排序中包含limit语句,则使用堆排序优化排序过程
代码实现地址:
https://github.com/xiaof-github/learn-alg
用go语言实现
时间复杂度
最基础的四个算法:冒泡、选择、插入、快排中,快排的时间复杂度最小O(n*log2n),其他都是O(n^2)
| 排序法 | 平均时间 | 最差情形 | 稳定度 | 额外空间 | 备注 |
| 冒泡 | O(n^2) | O(n^2) | 稳定 | O(1) | n小时较好 |
| 选择 | O(n^2) | O(n^2) | 不稳定 | O(1) | n小时较好 |
| 插入 | O(n^2) | O(n^2) | 稳定 | O(1) | 大部分已排序时较好 |
| 基数 | O(d(r+n)) | O(d(r+n)) | 稳定 | O(rd+n) |
B是真数(0-9), R是基数(个十百) |
| Shell | O(nlogn) | O(ns) 1<s<2 | 不稳定 | O(1) | s是所选分组 |
| 快速 | O(nlogn) | O(n^2) | 不稳定 | O(log2n)~O(n) | n大时较好 |
| 归并 | O(nlogn) | O(nlogn) | 稳定 | O(n) | n大时较好 |
| 堆 | O(nlogn) | O(nlogn) | 不稳定 | O(1) | n大时较好 |
执行速度比较
选用10万个随机数,进行排序
冒泡排序,耗时13411ms
归并排序,耗时34ms
快速排序,耗时9ms
对比这个数据来看,快速排序性能最好,实际要看数据分布。归并和快速排序的性能是一个量级的。
堆排序,耗时20248ms,还需要优化
优化后堆排序耗时 9ms:
冒泡排序实现
思路:
从第一个数开始,依次和后面的数比较,通过交换的方法,将最大的数交换到最后的位置。再继续从头以上述方式调整最大数的位置,直到调整到第二个数。
实现:
package main
import "log"
func main(){
var a = []int{45,145,245,32,5,2,69,239,12,40}
log.Print("before: ",a)
bubblesort(a)
log.Print("after: ",a)
}
/**
* 思路:从第一个数开始,依次和后面的数比较,通过交换的方法,将最大的数交换到最后的位置。再继续从头以上述方式调整最大数的位置,直到调整到第二个数。
*/
func bubblesort(arr []int){
for i:=len(arr);i>0;i-- {
for j:=0;j<i-1;j++ {
if (arr[j] > arr[j+1]){
swap(arr, j, j+1)
}
}
}
}
func swap(arr []int, j int, k int){
tmp := arr[j]
arr[j] = arr[k]
arr[k] = tmp
}
快速排序实现
思路:
以轴心调整数组中的数的位置,将小于轴心的数移动到左边,大于轴心的数移动到右边。
轴心将数分成两堆,再继续按上述的方法调整两堆数的位置,直到不能调整,此时排序完成。
以第一个数为轴心的实现:
package main
import "log"
func main(){
var a = []int{45,145,245,32,5,2,69,239,12,40}
log.Print("before: ", a)
quicksort(a)
log.Print("after: ", a)
}
/**
* 思路:以轴心调整数组中的数的位置,将小于轴心的数移动到左边,大于轴心的数移动到右边。
* 轴心将数分成两堆,再继续按上述的方法调整两堆数的位置,直到不能调整,此时排序完成。
*/
func quicksort(array []int){
left := 1
right := len(array)-1
swapedL := false
swapedR := false
// 轴心
zhou := array[0]
if(len(array) == 1){
log.Println(array)
return
}
if (len(array) == 2) {
if (array[0] > array[1]){
swap(array,0,1)
}
log.Println(array)
return
}
for ;left<right;{
if (zhou < array[left]){
swapedL = true
}else {
left++
}
if (zhou > array[right]){
swapedR = true
} else {
right--
}
if (swapedL && swapedR){
swap(array, left, right)
left++
right--
swapedL = false
swapedR = false
}
}
log.Println(left, right, array)
// 如果不交换,轴的大小顺序和数组中大小顺序不一致
if (zhou > array[right]){
swap(array, 0, right)
}
log.Println(array)
quicksort(array[0:right])
quicksort(array[right:len(array)])
}
func swap(array []int, i int, j int){
var tmp int
tmp = array[i]
array[i] = array[j]
array[j] = tmp
}
归并排序实现
实现了一版非递归的方式,思路是:
1.逐层分割原数组为两个元素的子序列,记录每个子序列中包含元素的个数
2.从最下一层开始,对每一层的子序列进行排序,并合并为上一层的子序列个数
3.重复步骤2,直到合并完第一层序列。
分割子序列个数举例:
* 切分子序列:确定每层的分割序列个数,直到子序列都为1个元素为止
10个元素:
1层:[[5,5]]
2层:[[2,3],[2,3]]
3层:[[1,1],[1,2],[1,1],[1,2]]
4层:[[1,1],[1],[1,1],[1,1],[1],[1,1]]
19个元素:
1层:[[9,10]]
2层:[[4,5],[5,5]]
3层:[[2,2],[2,3],[2,3],[2,3]]
4层:[[1,1],[1,1],[1,1],[1,2],[1,1],[1,2],[1,1],[1,2]]
5层:[[1,1],[1,1],[1,1],[1],[1,1],[1,1],[1],[1,1],[1,1],[1],[1,1]]
实现:
package main
import (
"log"
"math"
)
func main(){
var a = []int{45,145,245,32,5,2,69,239,12,40}
log.Print("before: ", a)
mergesort(a)
log.Print("after: ", a)
}
/**
* 思路: 逐层分割为两个元素的子序列,对子序列进行排序,对排序完的子序列从下到上进行合并
* 切分子序列:确定每层的分割序列个数,直到子序列都为1个元素为止
* 10个元素:[[5,5]],[[2,3],[2,3]],[[1,1],[1,2],[1,1],[1,2]],[[1,1],[1],[1,1],[1,1],[1],[1,1]]
* 19个元素:[[9,10]],[[4,5],[5,5]],[[2,2],[2,3],[2,3],[2,3]],[[1,1],[1,1],[1,1],[1,2],[1,1],[1,2],[1,1],[1,2]],[[1,1],[1,1],[1,1],[1],[1,1],[1,1],[1],[1,1],[1,1],[1],[1,1]]
* 排序和归并:两个游标移动,对两个切片中的数据排序后,合为一个切片
*/
func divide(arr []int) map[int][][]int {
subPos := make(map[int][][]int)
seqUnit := make([]int, 2)
seqUnit[0] = len(arr)/2
seqUnit[1] = len(arr) - len(arr)/2
subPos[0] = append(subPos[0], seqUnit)
lastLayerLen := 1
layerLen := lastLayerLen*2
layerNum := int(math.Ceil(math.Log2(float64(len(arr)))))
log.Print("layerNum: ", layerNum)
for i:=1;i<layerNum;i++ {
seq := subPos[i]
for j:=0;j<lastLayerLen;j++{
lastSeqUnit := subPos[i-1][j]
var seqUnit1,seqUnit2 []int
if (lastSeqUnit[0] == 1 && lastSeqUnit[1] == 2){
seqUnit1 = make([]int, 1)
seqUnit1[0] = 1
seqUnit2 = make([]int, 2)
seqUnit2[0] = 1
seqUnit2[1] = 1
} else if (lastSeqUnit[0] == 1 && lastSeqUnit[1] == 1){
seqUnit1 = make([]int, 2)
seqUnit1[0] = 1
seqUnit1[1] = 1
seqUnit2 = nil
} else {
seqUnit1 = make([]int, 2)
seqUnit1[0] = lastSeqUnit[0]/2
seqUnit1[1] = lastSeqUnit[0]-lastSeqUnit[0]/2
seqUnit2 = make([]int, 2)
seqUnit2[0] = lastSeqUnit[1]/2
seqUnit2[1] = lastSeqUnit[1]-lastSeqUnit[1]/2
}
seq = append(seq, seqUnit1)
if (seqUnit2 != nil){
seq = append(seq, seqUnit2)
}
}
lastLayerLen = lastLayerLen*2
layerLen = layerLen*2
subPos[i] = seq
log.Print("divide: ", subPos[i])
}
return subPos
}
func mergesort(arr []int) {
layer := divide(arr)
lenM := len(layer)
for i:=lenM-1;i>=0;i-- {
seq := layer[i]
base := 0
for j:=0;j<len(seq);j++ {
if (len(seq[j]) == 2) {
arrL := arr[base : base + seq[j][0]]
arrR := arr[base + seq[j][0] : base + seq[j][0] + seq[j][1]]
sort(arrL,arrR)
base += seq[j][0] + seq[j][1]
}else{
base += 1
}
}
}
return
}
func sort(arrL []int, arrR []int) {
tempSlice := make([]int, 0, len(arrL)+len(arrR))
for i,j:=0,0;;{
if ( i == len(arrL)) {
for ;j<len(arrR);j++ {
tempSlice = append(tempSlice, arrR[j])
}
break
}
if ( j == len(arrR)) {
for ;i<len(arrL);i++ {
tempSlice = append(tempSlice, arrL[i])
}
break
}
if (arrL[i] <= arrR[j]){
tempSlice = append(tempSlice, arrL[i])
i++
} else {
tempSlice = append(tempSlice, arrR[j])
j++
}
}
copy(arrL, tempSlice[0:len(arrL)])
copy(arrR, tempSlice[len(arrL):len(arrL) + len(arrR)])
// log.Print("tempSlice: ", tempSlice)
}
递归方式:
思路:
准备一个辅助数组。
1.将原数组分成两个序列,依次递归遍历两个序列,再对两个序列排序归并
2.归并时,将排序后的合并序列放入到辅助数组中,并以结果序列为起始再次排序归并
实现:
package main
import (
"log"
"math"
"time"
)
var sort2result []int
func main(){
var a = []int{45,145,245,32,5,2,69,239,12,40}
sort2result = make([]int, len(a))
// sort2result = make([]int, len(b))
log.Print("before: ", a)
start := time.Now().UnixNano()
mergesort2(a, 0, len(a) - 1)
// mergesort2(b, 0, len(b) - 1)
end := time.Now().UnixNano()
log.Print("after: ", a)
Milliseconds:= float64((end - start) / 1e6)
log.Print("start_time, end_time, cost: ", start, end, Milliseconds)
}
/*
* 递归思路: 准备一个辅助数组。
* 1.将原数组分成两个序列,依次递归遍历两个序列,再对两个序列排序归并
* 2.归并时,将排序后的合并序列放入到辅助数组中,并以结果序列为起始再次排序归并
*/
func mergesort2(arr []int, left int, right int) {
if (right == left){
return
}
if (right > left){
mergesort2(arr, left, (left+right)/2)
mergesort2(arr, (left+right)/2 + 1, right)
}
for i,j,k:=left,(left+right)/2 + 1,left;k<right + 1;k++{
if (i>(left+right)/2){
sort2result[k] = arr[j]
j++
continue
}
if (j>right){
sort2result[k] = arr[i]
i++
continue
}
if (arr[i] > arr[j]){
sort2result[k] = arr[j]
j++
} else {
sort2result[k] = arr[i]
i++
}
}
copy(arr[left:right+1], sort2result[left:right+1])
}
对比非递归方式,递归方式确实简单易懂很多。
堆排序实现
堆的定义:堆是完全二叉树,树里面的所有父节点都大于(或小于)左右子节点
堆举例:排序成数组时,从每一层按层序遍历将节点值填入数组,如最大堆可表示为数组:[9,7,6,3,2,5]
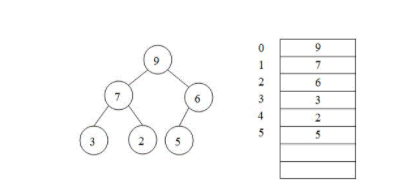
堆排序的过程是首先建立大顶堆(或者小顶堆),这个堆的特征是根节点不大于(或者不小于)任何子节点。建立之后就可以通过每次取出堆中的第一个元素(这个堆的最小值或最大值)然后将新的堆调整从而下次再取第一个这种循环操作来得到一个有序的序列。
实现思路:
1.首先将当前数组交换位置变成一个大顶堆,然后取大顶堆的堆首,交换到堆尾。
此时最大的数已被排序到数组尾,接下来将数组的元素减少一个,对arr[0:len-1]继续排序
2.将当前数组调整成一个最大堆,然后取最大堆的堆首,交换到堆尾。
3.重复步骤2,直到数组元素都排序完
实现:
package main
import (
"log"
"time"
)
func main(){
var a = []int{45,145,245,32,5,2,69,239,12,40}
log.Print("before: ", a)
start := time.Now().UnixNano()
heapsort(a)
end := time.Now().UnixNano()
log.Print("after: ", a)
Milliseconds:= float64((end - start) / 1e6)
log.Print("start_time, end_time, cost: ", start, end, Milliseconds)
}
func heapsort(arr []int) {
len := len(arr)
buildMaxHeap(arr)
swap(arr, 0, len-1)
for i := len-1;i>0;i-- {
heapify(arr[0:i], 1)
swap(arr[0:i], 0, i-1)
}
}
func buildMaxHeap(arr []int) {
lenH := len(arr)
for i:=lenH/2;i>0;i-- {
heapify(arr,i)
}
}
func swap(arr []int, i int, j int) {
temp := arr[i]
arr[i] = arr[j]
arr[j] = temp
}
/*
* 指定位置的节点按最大堆调整
*
*/
func heapify(arr []int, heap int) {
if (heap>len(arr) || heap*2>len(arr)){
return
}
// 比较左子节点
if (arr[heap-1] < arr[2*heap-1]) {
swap(arr, heap-1, 2*heap-1)
}
// 比较右子节点
if (heap*2+1>len(arr)) {
return
}
if (arr[heap-1] < arr[2*heap]) {
swap(arr, heap-1, 2*heap)
}
// 子节点
heapify(arr, 2*heap)
heapify(arr, 2*heap+1)
}
优化后的实现:
package main
// package test
import (
"log"
"time"
)
func main(){
var a = []int{45,145,245,32,5,2,69,239,12,40}
log.Print("before: ", a)
start := time.Now().UnixNano()
// heapsort(bA)
heapsort(a)
end := time.Now().UnixNano()
// log.Print("after: ", bA)
log.Print("after: ", a)
Milliseconds:= float64((end - start) / 1e6)
log.Print("start_time, end_time, cost: ", start, end, Milliseconds)
}
func heapsort(arr []int) {
len := len(arr)
buildMaxHeap(arr)
for i := len-1;i>0;i-- {
swap(arr, 0, i)
heapify1(arr, 0, i)
}
}
func buildMaxHeap(arr []int) {
lenH := len(arr)
for i:=lenH/2-1;i>=0;i-- {
// heapify(arr,i)
heapify1(arr, i, lenH)
}
}
func swap(arr []int, i int, j int) {
temp := arr[i]
arr[i] = arr[j]
arr[j] = temp
}
/*
* 指定位置的节点按最大堆调整
*
*/
func heapify(arr []int, heap int) {
if (heap>len(arr) || heap*2>len(arr)){
return
}
// 比较左子节点
if (arr[heap-1] < arr[2*heap-1]) {
swap(arr, heap-1, 2*heap-1)
}
// 比较右子节点
if (heap*2+1>len(arr)) {
return
}
if (arr[heap-1] < arr[2*heap]) {
swap(arr, heap-1, 2*heap)
}
// 子节点
heapify(arr, 2*heap)
heapify(arr, 2*heap+1)
}
func heapify1(arr []int, i int, length int) {
tmp := arr[i]
for k:=2*i+1;k<length;k=k*2+1 { //从i节点的左子节点开始,从2i+1处开始
if (k+1<length && arr[k] < arr[k+1]) { //如果左子节点小于右子节点,k指向右子节点
k++;
}
if (arr[k] > tmp) { //如果子节点大于父节点,将子节点的值赋给父节点(不用进行交换)
arr[i] = arr[k]
i = k
}else{
break
}
}
arr[i] = tmp //最后交换
}