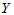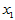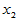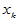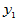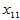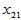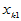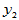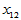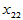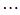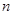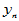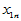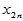4.1 一元回归分析
4.1.1 回归方程的计算
在高等数学中,研究函数两个变量的关系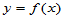 ,它们是确定的关系,当自变量
,它们是确定的关系,当自变量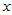 取定后,
取定后,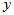 随之唯一确定。现实中,两个变量
随之唯一确定。现实中,两个变量 与
与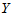 经常有相关关系。
经常有相关关系。
例4.1 研究化肥用量与小麦产量之间的关系,试种7块,每块一亩,得到实验数据(单位kg):
化肥用量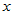 :15, 20, 25, 30, 35, 40, 45
:15, 20, 25, 30, 35, 40, 45
小麦产量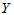 :330, 345, 365, 405, 445, 490, 455
:330, 345, 365, 405, 445, 490, 455
做出散点图,发现这些散点大致在一条直线附近,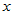 与
与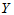 有近似关系式
有近似关系式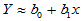 ,误差
,误差 可以认为是其它随机因素引起的。即:
可以认为是其它随机因素引起的。即:
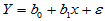 (4-1)
(4-1)
将上述模型称为一元线性回归模型,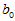 与
与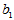 称为回归系数,直线
称为回归系数,直线
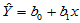 (4-2)
(4-2)
称为回归直线,对于固定的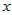 值,称
值,称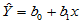 为回归值,
为回归值,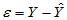 称为随机误差。将
称为随机误差。将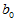 与
与 看成是可以选择的自变量,对于实验数据
看成是可以选择的自变量,对于实验数据
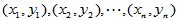
考虑随机误差的平方和,即
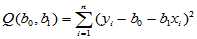 (4-3)
(4-3)
利用二元函数求极大值的方法,将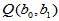 对两个自变量分别求偏导数,为求驻点,解方程组:
对两个自变量分别求偏导数,为求驻点,解方程组:
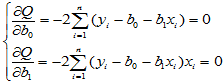
易得
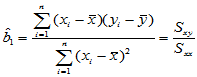 ,
,  (4-4)
(4-4)
由此确定的值能够使得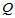 取极小值,从而确定回归方程
取极小值,从而确定回归方程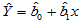 ,这种确定回归方程的方法称为最小二乘法。以下用Matlab命令求例4.1的回归方程:
,这种确定回归方程的方法称为最小二乘法。以下用Matlab命令求例4.1的回归方程:
x=[15, 20, 25, 30, 35, 40, 45];
y=[330, 345, 365, 405, 445, 490, 455];
xx=x-mean(x);
yy=y-mean(y);
sxy=sum(xx.*yy);
sxx=sum(xx.^2);
b1=sxy/sxx
b0=mean(y)-b1*mean(x)
经计算,得到回归系数,回归方程为
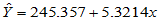
4.1.2 回归方程的显著性检验
上面给出了回归方程的计算方法,从化肥用量-小麦产量的回归方程中可以看出,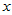 与
与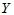 有正相关关系,在一定范围内,化肥多则产量高。由于回归方程的计算对于任意一组散点都能进行,很可能
有正相关关系,在一定范围内,化肥多则产量高。由于回归方程的计算对于任意一组散点都能进行,很可能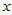 与
与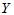 客观上没有正(负)相关关系,我们也会有模有样地计算出一个回归方程来。为此,我们进行如下的假设检验:
客观上没有正(负)相关关系,我们也会有模有样地计算出一个回归方程来。为此,我们进行如下的假设检验:
H0: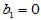 ; H1:
; H1: ;
;
这样,当我们拒绝原假设的时候,就可以说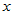 与
与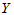 确有相关关系,回归方程是有意义的。
确有相关关系,回归方程是有意义的。
为了进行上述检验,首先必须保证随机误差 ,其中方差有如下估计量:
,其中方差有如下估计量:
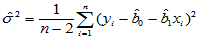 (4-5)
(4-5)
在前述Matlab命令已经执行的基础上,继续例4.1的计算
n=length(x);
yh=b0+b1*x;
s2=sum((y-yh).^2)/(n-2);
s1=sqrt(s2)
得到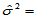 465.5357,
465.5357,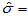 21.5763
21.5763
可以证明,当H0成立时,检验统计量
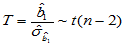 (4-6)
(4-6)
其中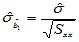 。
。
取临界值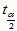 ,当
,当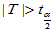 时拒绝H0成,认为
时拒绝H0成,认为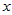 与
与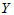 存在相关关系,回归方程有意义。
存在相关关系,回归方程有意义。
继续例4.1的计算:
sb1=s1/sqrt(sxx);
T=b1/sb1;
alpha=0.05;
t0=tinv(1-alpha/2,n-2);
Tt=[T,t0]
得到结果为 T=6.5253>t0=2.5706,因此拒绝H0成,认为 与
与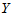 存在相关关系,回归方程有意义。
存在相关关系,回归方程有意义。
以下将上述过程编制一个函数文件,求一元线性回归方程,连带进行显著性检验。调用格式为:
[b0,b1,H]=reg1(x,y,alpha)
其中为x,y实验数据,注意保证个数相等。alpha是检验的显著性水平,常用值为0.05。三个输入变量必须赋值后才可调用此函数。三个输出:b0为回归常数,b1为回归系数,H为显著性检验判定值,H=1表示回归方程显著有意义,H=0表示回归方程不显著、无意义。
function [b0,b1,H]=reg1(x,y,alpha)
m=length(x);
n=length(y);
if m~=n
disp('Be sure Nx=Ny>>>>>>>>>>>>>STOP');
else
[m,n]=size(x);
if m>n
x=x';
end
[m,n]=size(y);
if m>n
y=y';
end
xx=x-mean(x);
yy=y-mean(y);
sxy=sum(xx.*yy);
sxx=sum(xx.^2);
b1=sxy/sxx;
b0=mean(y)-b1*mean(x);
n=length(x);
yh=b0+b1*x;
s2=sum((y-yh).^2)/(n-2);
s1=sqrt(s2);
sb1=s1/sqrt(sxx);
T=b1/sb1;
t0=tinv(1-alpha/2,n-2);
H=0;
if T>t0
H=1;
end
end
至此函数文件结束。
4.2 多元回归分析
4.2.1 多元回归方程的计算
高等数学中有多元函数的概念,类似地变量 可能与多个变量
可能与多个变量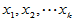 具有线性相关关系,即满足如下的多元线性模型:
具有线性相关关系,即满足如下的多元线性模型:
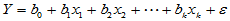 ,
, 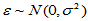 (4-7)
(4-7)
其中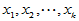 是可控变量,我们常常可以选择这些变量的值做实验,不是随机变量。
是可控变量,我们常常可以选择这些变量的值做实验,不是随机变量。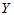 由于受到了随机误差的干扰,因而是随机变量,即使诸
由于受到了随机误差的干扰,因而是随机变量,即使诸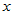 都确定,
都确定, 也会有随机波动。样本容量为
也会有随机波动。样本容量为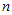 的实验数据如表4-1所示。
的实验数据如表4-1所示。
表4-1 多元线性模型数据表
实验序号 |
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
| |||||
|
|
|
|
|
|
上述关系可用矩阵的形式表示为
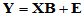 (4-8)
(4-8)
其中
 ,
, 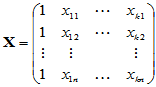 ,
, 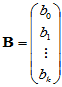 ,
, 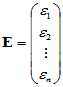
对此,仿照一元线性回归的方法,令误差平方和
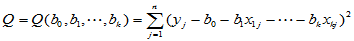 (4-9)
(4-9)
取得极小值,通过求偏导数,令每个偏导数为零解方程组,可得极小值点,即回归系数的最小二乘估计:
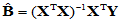 (4-10)
(4-10)
由此可以确定多元线性模型中的系数,得到多元线性回归方程:
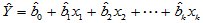 (4-11)
(4-11)
由此计算出的数值
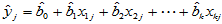 ,
, 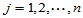 (4-12)
(4-12)
称为回归值。
(4-10)式为矩阵形式,特别适合Matlab计算。
4.2.2 显著性检验
(1)回归方程的显著性检验
H0: 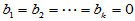 ; H1: 至少有一个
; H1: 至少有一个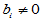
记
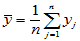 ,
,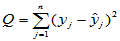 ,
,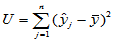 (4-13)
(4-13)
取检验统计量为:
 (4-14)
(4-14)
可以证明, H0成立时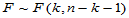 ,找临界值
,找临界值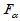 ,使得
,使得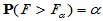 。当
。当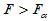 时拒绝H0,认为回归方程有意义。
时拒绝H0,认为回归方程有意义。
(2)每个回归系数的显著性检验
对于回归方程的显著性检验即使通过,也不能保证每个变量的系数都不为零,或许有滥竽充数者,为此,需要对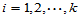 逐个检验如下假设:
逐个检验如下假设:
H0:  ; H1:
; H1: 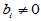
记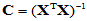 ,这是一个
,这是一个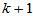 阶方阵,将其对角元记为
阶方阵,将其对角元记为
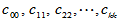
可以证明,当H0成立时
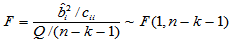 (4-15)
(4-15)
对于给定的显著性水平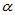 ,
,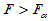 时拒绝H0,认为
时拒绝H0,认为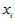 对
对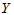 有显著影响。也可计算
有显著影响。也可计算
pi=1-fcdf(F,1,n-k-1)
此值小于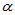 时拒绝H0,认为
时拒绝H0,认为 对
对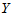 有显著影响。pi越小,
有显著影响。pi越小,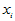 对
对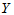 影响越显著,由此可以排列各自变量的重要程度。
影响越显著,由此可以排列各自变量的重要程度。
以下将回归方程的求法及显著性检验合并起来,定义函数regk.m文件保存。
function [NBP,H]=regk(yx,alpha)
[n,K]=size(yx);
k=K-1;
P=zeros(K,1);
y=yx(:,1);
x=yx;
x(:,1)=ones(n,1);
B=inv(x'*x)*(x'*y);
my=mean(y);
yc=x*B;
yu=yc-my;
U=yu'*yu;
E=y-x*B;
Q=E'*E;
F=(U/k)/(Q/(n-k-1));
Fa=finv(1-alpha,k,n-k-1);
H=0;
if F>Fa
H=1;
end
C=inv(x'*x);
for i=2:K
G(i)=(B(i)^2/C(i,i))/(Q/(n-K));
P(i)=1-fcdf(G(i),1,n-K);
end
BP=[B,P];
N=0:K-1; N=N';
NBP=[N,BP];
[PP,I]=sort(P);
NBP=NBP(I,:);
例4.2 某观测区域内连续13年观测某种害虫的成虫数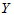 ,发现与如下四个因素有关:
,发现与如下四个因素有关: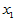 为冬季积雪周数,
为冬季积雪周数,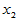 化雪日期(2月1日记为1),
化雪日期(2月1日记为1),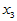 二月平均气温(oC),
二月平均气温(oC),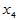 三月平均气温(oC)。试建立用诸
三月平均气温(oC)。试建立用诸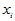 预测该种害虫成虫数的回归方程,并做显著性检验。
预测该种害虫成虫数的回归方程,并做显著性检验。
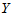
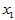
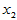
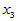
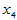
9.0000 10.0000 26.0000 0.2000 3.6000
17.0000 12.0000 26.0000 -1.4000 4.4000
34.0000 14.0000 40.0000 -0.8000 1.7000
42.0000 16.0000 32.0000 0.2000 1.4000
40.0000 19.0000 51.0000 -1.4000 0.9000
27.0000 16.0000 33.0000 0.2000 2.1000
4.0000 7.0000 26.0000 2.7000 2.7000
27.0000 7.0000 25.0000 1.0000 4.0000
13.0000 12.0000 17.0000 2.2000 3.7000
56.0000 11.0000 24.0000 -0.8000 3.0000
15.0000 12.0000 16.0000 -0.5000 4.9000
8.0000 7.0000 16.0000 2.0000 4.1000
20.0000 11.0000 15.0000 1.1000 4.7000
解 鼠标选中复制上述数据方阵,在Matlab命令窗口中输入yx=[],将光标点到方括号中间,粘贴,回车执行。于是数据输入完毕。在上述regk.m文件已经保存的前提下,键入命令:
[NBP,H]=regk(yx,0.05)
得到输出结果。
NBP =
0 138.0710 0
3.0000 -11.1886 0.0204
4.0000 -16.9790 0.0295
2.0000 -1.6584 0.0805
1.0000 -1.0088 0.4990
H =
1
上面的输出结果说明回归方程为:
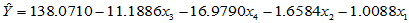
回归方程显著。依照影响的重要程度, 与
与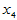 显著,
显著,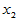 不显著,
不显著,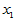 最不显著。
最不显著。
4.2.3 逐步回归分析
例4.2给出了回归方程,方程显著,但存在两个不显著的变量。逐步回归的想法是,有不显著的变量,则删除最不显著的一个变量,看看剩余的变量是否显著,如果有不显著的继续删除,直到剩余的全部显著为止。前面已经删除的变量还可继续引入,直到所有的变量都显著,并且再添加任意一个变量都不显著,到此结束。
先给出单纯删除变量的函数regcut.m,其中yes是输入变量,也是输出变量,为k+1阶行向量,其中元素为0或者1,第一个数yes(1)永为1,表示常数项不删除,其余表示各个自变量是否入选。cut为输出变量,取值为0表示入选的自变量都显著,不能删除,取值1表示删除一个变量完毕,用输出的yes记录删除了哪个变量。仅仅剩余一个变量时,返回cut=0,表示就算不显著也不能删除了,最后根据逐步回归主程序判定是否保留。
function [cut,yes]=regcut(yes,yx,alpha)
% lenth(yes)=K=k+1, (1,K), yes(1)=1;
[n,K]=size(yx);
s=sum(yes);
if s<2.5
cut=0;
else
YX=[];
for i=1:K
if yes(i)>0
YX=[YX,yx(:,i)];
end
end
NBP=regk(YX,alpha);
[j,t]=size(NBP);
if NBP(j,3)<=alpha
cut=0;
else
cut=1;
ii=NBP(j,1);
S=0; kk=2;
while S<(ii-0.1)
S=S+yes(kk);
kk=kk+1;
end
kk=kk-1;
yes(kk)=0;
end
end
以下函数regadd.m给出了单纯添加变量的功能,输出变量add记录了添加变量的个数,yes记录了添加哪些变量。add=0表示无法添加任何变量。需要用到regcut.m,请依次保存。
function [add,yes]=regadd(yes,yx,alpha)
% lenth(yes)=K=k+1, (1,K), yes(1)=1;
[n,K]=size(yx);
s=sum(yes);
YES=yes;
add=0;
if s<K
YX=[];
for i=1:K
if yes(i)>0
YX=[YX,yx(:,i)];
end
end
for j=2:K
if yes(i)<0.5
YES(i)=1;
[cut,YES]=regcut(YES,yx,alpha);
if cut<0.5
add=add+1;
yes(i)=1;
else
YES(i)=0;
end
end
end
end
有了前两个基础,下面给出逐步回归的函数,调用比较简单,返回的NBP有三列,分别记录了自变量原始标号,回归系数,显著性概率值p,并依照p由小到大逐行排列,反映了个自变量的重要程度依次排序。
function [yes,NBP]=regstep(yx,alpha)
[n,K]=size(yx);
k=K-1;
yes=ones(1,K);
cut=1;
add=0;
while (cut+add)>0.5
[cut,yes]=regcut(yes,yx,alpha);
if cut<0.5
[add,yes]=regadd(yes,yx,alpha);
end
end
YX=[];
for i=1:K;
if yes(i)>0.5
YX=[YX,yx(:,i)];
end
end
NBP=regk(YX,alpha);
[s,t]=size(NBP);
for i=2:s
SS=0; k=2;
while SS<NBP(i,1);
SS=SS+yes(k);
k=k+1;
end
NBP(i,1)=k-2;
end