第九章 几何连续性
关于参数曲线的光滑性有两种不同的度量,其一是多年来沿用的函数曲线的可微性,即通过参数曲线上一点处直到 阶的连续导矢来度量,这类连续性称之为
阶的连续导矢来度量,这类连续性称之为 连续。另一种称为几何连续性,即通过参数曲线上一点处满足不同于
连续。另一种称为几何连续性,即通过参数曲线上一点处满足不同于 的某一组约束条件来度量,称之为
的某一组约束条件来度量,称之为 连续。
连续。
9.1 参数连续性分析
由第四章的讨论,我们知道参数连续与所选取的参数有关。整体参数下的参数连续性条件与局部参数下的连续性条件就不相同。一方面,当各曲线段的Bézier点给定之后,各段曲线的形状随之完全确定。由此构成的B样条曲线的形状亦完全确定,自然在连接点处的光滑度亦确定不变,它与所选取参数节点矢量无关;另一方面,当两段曲线的公共连接点 与前后相邻Bézier点
与前后相邻Bézier点 重合时,那么B样条曲线在
重合时,那么B样条曲线在 处有零切矢,那么不管对于局部参数还是整体参数,曲线在该点都是
处有零切矢,那么不管对于局部参数还是整体参数,曲线在该点都是 连续的。然而,B样条曲线可能在该连接点处形成一尖角,因而是不光滑的。这表明,可微的参数曲线有可能是不光滑的。下面我们通过几个具体的例子进一步予以说明。
连续的。然而,B样条曲线可能在该连接点处形成一尖角,因而是不光滑的。这表明,可微的参数曲线有可能是不光滑的。下面我们通过几个具体的例子进一步予以说明。

例1对于曲线

 ,曲线在
,曲线在 处有零切矢,但却
处有零切矢,但却 连续。
连续。

例2 给定三个不重合的共线点 ,且
,且
 ,定义下述直线段:
,定义下述直线段:

则:
 ,
,
因此,直线段 在
在 不是
不是 连续,仅为
连续,仅为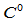 连续。
连续。

例3 给定曲线段:

在 处做
处做 的镜面映射得到曲线
的镜面映射得到曲线 ,那么
,那么 与
与 在公共连接点
在公共连接点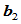 处具有连续的切线、曲率和法矢,但却不是
处具有连续的切线、曲率和法矢,但却不是 连续的。因为,如果
连续的。因为,如果 连续,则
连续,则 与
与 为同一抛物线的两段,而抛物线不可能有平行切矢。
为同一抛物线的两段,而抛物线不可能有平行切矢。
由此可以看出,采用参数连续性作为参数曲线的光滑性之度量具有以下明显的缺陷:
① 参数连续性与所选取的参数有关;
② 参数可微的曲线几何上不一定光滑;
③ 几何上光滑的曲线有可能是不可微的。
因之,参数连续性不能客观、准确地度量参数曲线的光滑性,而形状的客观内在几何特征是不依赖于参数的选取和具体参数化。正是由于此,CAD/CAM中人们才引入了称之为视觉连续的几何连续性,它与参数的选取和具体参数化无关,排除了由参数选取引起的非正则情况,只要求较弱的限制条件,且为形状定义和形状控制提供了额外的自由度。
9.2  连续性条件
连续性条件
曲率连续但非 连续的曲线称为
连续的曲线称为 连续。设
连续。设 是
是 连续的正则曲线,即
连续的正则曲线,即 ,
, 为
为 的弧长,那么对
的弧长,那么对 重新参数化,使得
重新参数化,使得 。曲率连续意味着
。曲率连续意味着 关于弧长的二阶导矢连续,即:
关于弧长的二阶导矢连续,即: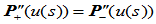 。由链导法则,有
。由链导法则,有

因
 连续且
连续且 ,所以
,所以 ,
,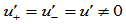 ,从而:
,从而:

即:

令 ,则有:
,则有:
 (9.2.1)
(9.2.1)
这就是曲线 的
的 连续条件,其几何意义如下:左右二阶导矢的差向量平行于
连续条件,其几何意义如下:左右二阶导矢的差向量平行于 。显然,正则的
。显然,正则的 连续的曲线都是
连续的曲线都是 连续的,此时
连续的,此时 。
。
对于分段多项式曲线 来说,若分割点为
来说,若分割点为 ,那么
,那么
 连续的条件是:
连续的条件是:
 (9.2.2)
(9.2.2)
此时,式(9.2.1)中的函数 可定义如下:
可定义如下:
 (9.2.3)
(9.2.3)
值得注意的是, 不是仿射不变量,因为若对
不是仿射不变量,因为若对 用
用 重新参数化,则有
重新参数化,则有 。
。
9.3 Nu三次样条曲线
给定 个型值点
个型值点 及参数分割
及参数分割 ,我们构造插值这些点的
,我们构造插值这些点的 三次样条曲线
三次样条曲线 。在区间
。在区间 上,
上, 被表示成三次Hermite形式:
被表示成三次Hermite形式:

其中 是三次Hermite基函数,
是三次Hermite基函数,  ,
, 是
是 处的切矢,是未知量。根据
处的切矢,是未知量。根据 连续性条件,在连接点
连续性条件,在连接点 处有:
处有:

这里 是任意常数,从而有:
是任意常数,从而有:
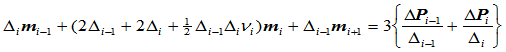 (9.3.1)
(9.3.1)
添加两个边界条件,即可求出所有未知的切矢 ,这样得到的三次样条曲线称为Nu样条曲线。
,这样得到的三次样条曲线称为Nu样条曲线。
Nu样条曲线比标准的 三次插值曲线更一般,一般情况下不再是
三次插值曲线更一般,一般情况下不再是 连续的。若令
连续的。若令 ,
, ,则得到标准的
,则得到标准的 三次样条曲线。
三次样条曲线。
如果令 ,则
,则 。由此可见,
。由此可见, 增大的效果是切矢
增大的效果是切矢 的模长减小。若所有的
的模长减小。若所有的 ,则所有的
,则所有的 ,样条曲线便趋于通过数据点的分段直线。所有
,样条曲线便趋于通过数据点的分段直线。所有 这种情况将使得样条曲线不再是
这种情况将使得样条曲线不再是 的,与最初假设曲线是正则的条件相背离。
的,与最初假设曲线是正则的条件相背离。
从 的值对曲线形状的影响来看,
的值对曲线形状的影响来看, 称为张力参数(tension parameter)。张力参数越大,曲线被拉得越紧。这些特性使其特别适合交互图形环境。
称为张力参数(tension parameter)。张力参数越大,曲线被拉得越紧。这些特性使其特别适合交互图形环境。
前面讨论 连续条件是从
连续条件是从 出发的,如直接从
出发的,如直接从 出发,那
出发,那 连续条件又是什么呢?
连续条件又是什么呢?
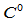 连续的参数曲线
连续的参数曲线 是
是 连续的,如果它是切向连续、曲率连续的,即:
连续的,如果它是切向连续、曲率连续的,即:

由链导规则,有:
 (9.3.2)
(9.3.2)
基于条件(9.3.2)构造的 三次插值样条曲线称为Manning三次插值曲线。若所有
三次插值样条曲线称为Manning三次插值曲线。若所有 ,则得到标准的
,则得到标准的 三次样条曲线。若所有
三次样条曲线。若所有 ,则得到Nu三次插值样条曲线。与Nu样条曲线相比,Manning样条曲线中,除了张力参数
,则得到Nu三次插值样条曲线。与Nu样条曲线相比,Manning样条曲线中,除了张力参数 外,还多出一个位移参数
外,还多出一个位移参数 (bias)。
(bias)。
9.4 参数曲线几何连续性定义
在讨论了特殊几何连续性的基础上,我们现在可进一步讨论它的一般定义。由于形状与描述它所选取的参数无关,因而作为形状内在几何特征的光滑性及其量度光滑性的几何连续定义自然应建立在独立于具体参数化的基础之上。
前面的讨论已给出了二阶几何连续性的定义,即: 连续与
连续与 连续一致;若两曲线在公共连接点处具有公共的单位切矢(切线方向),则称它们在该点处
连续一致;若两曲线在公共连接点处具有公共的单位切矢(切线方向),则称它们在该点处 连续;若在公共连接点处还具有公共的曲率矢,则称它们在该点处
连续;若在公共连接点处还具有公共的曲率矢,则称它们在该点处 连续。由此出发,即可定义一般的几何连续性。
连续。由此出发,即可定义一般的几何连续性。
为了保证几何连续性的定义与具体的参数化无关,只要将几何连续性的定义建立在曲线内在几何量的基础上即可。由微分几何可知,弧长是曲线的内在几何量,因而可借助弧长参数来建立几何连续性的定义。
定义9.1 如果两段曲线在相应弧长参数化下在公共连接点处 连续,则称它们在该点处
连续,则称它们在该点处 连续。或者换一种提法:一条曲线是
连续。或者换一种提法:一条曲线是 连续的,如果它关于弧长参数化是
连续的,如果它关于弧长参数化是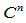 连续的。
连续的。
弧长是曲线的内在几何量,取弧长参数化使曲线的定义与参数无关。在弧长参数化下,切矢模长恒为1,这排除了非正则情况的出现。定义9.1表明,在弧长参数化下,几何连续性 与参数连续性
与参数连续性 是一致的,同时亦表明,对于一般参数表示的两段曲线,如果能够通过参数变换使它们在公共连接点处具有一致的直到
是一致的,同时亦表明,对于一般参数表示的两段曲线,如果能够通过参数变换使它们在公共连接点处具有一致的直到 阶的关于弧长的导矢,则它们在该点的连续阶就是
阶的关于弧长的导矢,则它们在该点的连续阶就是 的。然而,遗憾的是,并非所有的参数都能取自身的弧长作为参数。例如,非正则曲线就不能,CAD/CAM中广泛采用的参数多项式曲线和参数有理多项式曲线亦不能取自身的弧长作为参数,这就限制了这一定义的使用范围。为此,我们基于参数变换给出下面的几何连续性定义。
的。然而,遗憾的是,并非所有的参数都能取自身的弧长作为参数。例如,非正则曲线就不能,CAD/CAM中广泛采用的参数多项式曲线和参数有理多项式曲线亦不能取自身的弧长作为参数,这就限制了这一定义的使用范围。为此,我们基于参数变换给出下面的几何连续性定义。
定义9.2
若能将两曲线段之一经参数变换,重新参数化后使得它们在公共连接点处具有正则的 连续,则称它们在该点处是
连续,则称它们在该点处是 连续的。
连续的。
该定义有两层含义,其一是如果两正则曲线段在公共连接点处是 的,则必然是
的,则必然是 的;其二是如果两正则曲线段在公共连接点处是
的;其二是如果两正则曲线段在公共连接点处是 的,则总可以经过重新参数化使它们在公共连接点处
的,则总可以经过重新参数化使它们在公共连接点处 连续。
连续。
定义9.2的应用依赖于重新参数化,未给出现成可用的结果,仍然不够直接。为此,还需引入具有可操作性的等价定义。在给出等价定义之前,我们先介绍Beta约束。
Beta约束
由定义9.2,若两段曲线在公共连接点 处是
处是 的,则可对其中之一经过重新参数化使它们在该点具有正则的
的,则可对其中之一经过重新参数化使它们在该点具有正则的 连续。假设对公共点
连续。假设对公共点 左侧的曲线段
左侧的曲线段 做参数变换
做参数变换 ,使其重新参数化为
,使其重新参数化为 。那么,
。那么, 关于参数
关于参数 的直到
的直到 阶的导矢在
阶的导矢在 处应等于右侧曲线段
处应等于右侧曲线段 在
在 处关于参数
处关于参数 的直到
的直到 阶的导矢,因而由链导法则,可得到以下结果:
阶的导矢,因而由链导法则,可得到以下结果:

这里, 为曲线段
为曲线段 关于参数
关于参数 在
在 处的各阶导矢,
处的各阶导矢, 为曲线段
为曲线段 关于参数
关于参数 在
在 处的各阶导矢,
处的各阶导矢, 为参数变换
为参数变换 在
在 关于参数
关于参数 的各阶导数。
的各阶导数。
令 ,则可得到如下的用矩阵表示的一组关系式:
,则可得到如下的用矩阵表示的一组关系式:
 (9.4.1)
(9.4.1)
其中, ,
, 与
与 为公共连接点两侧的
为公共连接点两侧的 阶导矢。式(9.4.1)表明,在正则的公共连接点处,一侧的
阶导矢。式(9.4.1)表明,在正则的公共连接点处,一侧的 阶导矢可以表示成另一侧的直到
阶导矢可以表示成另一侧的直到 阶导矢的线性组合,这一组关系称为Beta约束,右端的
阶导矢的线性组合,这一组关系称为Beta约束,右端的 阶方阵称为关联矩阵。
阶方阵称为关联矩阵。
根据链导法则, 阶导矢
阶导矢 可显式地表示为:
可显式地表示为:
 (9.4.2)
(9.4.2)
其中:
 (9.4.3)
(9.4.3)
其求和是遍历整数 的分割
的分割 。如果
。如果 的一个分割中包含有
的一个分割中包含有 个不同元素,对应的重数为
个不同元素,对应的重数为 ,则
,则
 (9.4.4)
(9.4.4)
同样的参数曲线,若采用不同的整体参数或局部参数,仅仅关联矩阵中的非零元素不同而已。更确切地说, 取不同的值,它们由所选取的参数变换决定。这表明Beta约束与参数无关。
取不同的值,它们由所选取的参数变换决定。这表明Beta约束与参数无关。
几何连续性
利用Beta约束,我们可以定义一般地几何连续性。
定义9.3
当且仅当存在实数 ,使得两曲线段在正则的公共连接点处的直到
,使得两曲线段在正则的公共连接点处的直到 阶左、右导矢满足Beta约束(9.4.1)时,则称它们在该点处是
阶左、右导矢满足Beta约束(9.4.1)时,则称它们在该点处是 连续的。
连续的。
Beta约束的应用有以下几个方面:①
用于检查两曲线段在公共连接点处是否达到 连续;②
设计人员可以通过改变
连续;②
设计人员可以通过改变 的值来控制相邻两段曲线之一的形状,同时由使Beta约束得到满足,即曲线段间连接的光滑性得到保证。因之,
的值来控制相邻两段曲线之一的形状,同时由使Beta约束得到满足,即曲线段间连接的光滑性得到保证。因之, 称之为形状参数。这样当曲线用控制多边形定义时,无需改变控制多边形,只要改变参数
称之为形状参数。这样当曲线用控制多边形定义时,无需改变控制多边形,只要改变参数 便可改变曲线的形状。两曲线段间的
便可改变曲线的形状。两曲线段间的 连续性提供了
连续性提供了 个形状参数,对于参数多项式曲线而言,可调的形状参数不超过其次数。这些可调的形状参数提供了控制曲线形状的额外自由度,特别适合于人机交互环境下的曲线设计;③
构造Beta样条曲线。
个形状参数,对于参数多项式曲线而言,可调的形状参数不超过其次数。这些可调的形状参数提供了控制曲线形状的额外自由度,特别适合于人机交互环境下的曲线设计;③
构造Beta样条曲线。
采用Beta约束的几何连续性定义,尽管提供了直接可用的结果,但应当注意的是几何连续性定义是用代数形式的Beta约束给出的,其中的形状参数 几何意义不明显。那么,能否用纯几何的方式来刻画几何连续性呢?下面就来回答这一问题。
几何意义不明显。那么,能否用纯几何的方式来刻画几何连续性呢?下面就来回答这一问题。
实际上,定义9.3就是微分几何中的 阶切触。根据切触的定义,两曲线段在公共连接点处具有
阶切触。根据切触的定义,两曲线段在公共连接点处具有 阶切触,则它们在该点具有一致的直到
阶切触,则它们在该点具有一致的直到 阶的关于弧长的导矢,这与定义9.1相吻合。而两曲线段在公共连接点处的
阶的关于弧长的导矢,这与定义9.1相吻合。而两曲线段在公共连接点处的 阶切触,亦可由与两曲线段在该点处有
阶切触,亦可由与两曲线段在该点处有 公共点的一条
公共点的一条 次密切抛物线来定义,这在解析上意味着两曲线段之一能被重新参数化,一致于它们是
次密切抛物线来定义,这在解析上意味着两曲线段之一能被重新参数化,一致于它们是 连续的,这与定义9.2完全一样。
连续的,这与定义9.2完全一样。
执行重新参数化过程,设对公共连接点 左侧的那一段曲线
左侧的那一段曲线 进行重新参数化
进行重新参数化 ,将其在
,将其在 处Taylor展开:
处Taylor展开:

其中, 。与前述相同,使重新参数化后的左侧曲线段
。与前述相同,使重新参数化后的左侧曲线段 与右侧的曲线段
与右侧的曲线段 在公共点
在公共点 处
处 连续,即
连续,即 在
在 处关于参数
处关于参数 的直到
的直到 阶导矢与
阶导矢与 关于
关于 的直到
的直到 阶导矢相同。由链导法则就可得到一组约束,即Beta约束,这就是定义9.3。因而,本质上说,两曲线段在公共连接点的
阶导矢相同。由链导法则就可得到一组约束,即Beta约束,这就是定义9.3。因而,本质上说,两曲线段在公共连接点的 连续就是几何意义下的
连续就是几何意义下的 阶切触,故便有下述的等价定义。
阶切触,故便有下述的等价定义。
定义9.4
当且仅当两曲线段在公共连接点处具有 阶切触,则称它们在该点
阶切触,则称它们在该点 连续。
连续。
CAD/CAM中常用的曲线是参数多项式曲线及由几何连续拼接而成的样条曲线。由于参数多项式曲线在一点的Tayor展开是精确的,因此如果两段参数 曲线在公共连接点处具有直到
曲线在公共连接点处具有直到 阶的相同导矢,则它们实际上是同一条曲线。
阶的相同导矢,则它们实际上是同一条曲线。
三维空间的参数曲线在一点处的 阶切触的几何意义是:设
阶切触的几何意义是:设 分别为曲线上该点处的单位切矢、主法矢和副法矢,它们构成曲线上该点的Frenet标架,
分别为曲线上该点处的单位切矢、主法矢和副法矢,它们构成曲线上该点的Frenet标架, 分别表示曲线在该点的曲率和挠率,那么曲线在该点处关于弧长的二、三、四阶导矢分别为:
分别表示曲线在该点的曲率和挠率,那么曲线在该点处关于弧长的二、三、四阶导矢分别为:

显然,二阶切触等价于连续的Frenet标架和连续的曲率,三阶切触等价于连续的Frenet标架、 连续的曲率和连续的挠率,四阶切触等价于连续的Frenet标架、
连续的曲率和连续的挠率,四阶切触等价于连续的Frenet标架、 连续的曲率和
连续的曲率和 连续的挠率。因此,
连续的挠率。因此, 阶切触等价于连续的Frenet标架、
阶切触等价于连续的Frenet标架、 连续的曲率和
连续的曲率和 连续的挠率。
连续的挠率。
由此可见,用Beta约束定义的几何连续性与 阶切触相一致,讨论了数十年之久的连续性问题由回到了经典微分几何中早已给出的答案之上来,但这不是简单地重复,而是认识真理过程的螺旋上升运动。
阶切触相一致,讨论了数十年之久的连续性问题由回到了经典微分几何中早已给出的答案之上来,但这不是简单地重复,而是认识真理过程的螺旋上升运动。
几何连续的组合Bézier曲线
9.5.1 Bézier曲线 连续的几何关系
连续的几何关系
给定两条n次Bézier曲线:

在公共连接点 处
处 连续条件为:
连续条件为:
 或
或 (9.5.1)
(9.5.1)
即三点 共线,且顺序排列。
共线,且顺序排列。

两曲线在公共连接点 处的曲率分别为
:
处的曲率分别为
:

其中 ,
, 分别为
分别为 和
和 到
到 处公切线的距离,如图9.4所示。
处公切线的距离,如图9.4所示。
视 为直角三角形的直角顶点,
为直角三角形的直角顶点, 为斜边的高,分斜边成长为
为斜边的高,分斜边成长为 和
和 两部分,则有
两部分,则有 。类似地,有
。类似地,有 。于是有:
。于是有:

那么,在公共连接点 处两曲线段曲率相等的条件除式(9.5.1)外,还满足下述条件:
处两曲线段曲率相等的条件除式(9.5.1)外,还满足下述条件:
 或
或  或
或  (9.5.2)
(9.5.2)
要使 处两曲线段的曲率矢量相同,不仅曲率相等还应有公共的密切平面。这意味着五点
处两曲线段的曲率矢量相同,不仅曲率相等还应有公共的密切平面。这意味着五点 共面,且
共面,且 位于
位于 处切线的同侧,这便是
处切线的同侧,这便是 连续性条件。
连续性条件。
在保持公共连接点处 连续,且曲率值与
连续,且曲率值与 位置不变的条件下,顶点
位置不变的条件下,顶点 可分别在平行于公共切线的直线上移动。欲使
可分别在平行于公共切线的直线上移动。欲使 移动到
移动到 而保持公共连接点处的曲率不变,则必须同时使点
而保持公共连接点处的曲率不变,则必须同时使点 在平行于公共切线的另一直线上移动。
在平行于公共切线的另一直线上移动。
现假设这两条n次Bézier曲线采用整体参数表示,相应的参数分别为 ,且约定在公共连接点
,且约定在公共连接点 处关于整体参数
处关于整体参数 是
是 连续的,那么:
连续的,那么:

即: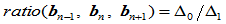 。
。
如果还要求是 连续的,则有:
连续的,则有:

两边用 做叉乘,有:
做叉乘,有:

由此得到:

根据 连续条件
连续条件 ,可知:
,可知:

代入上式,有

因而可得整体参数下 连续曲线,其
连续曲线,其 连续条件为
连续条件为
 (9.5.3)
(9.5.3)
其中area表示有向面积。
第一式意味着五点 共面,第二式隐含了点且
共面,第二式隐含了点且 与
与 位于
位于 处切线的同侧。
处切线的同侧。
9.5.2  组合三次Bézier曲线的构造
组合三次Bézier曲线的构造
回顾设4.5节关于 组合三次Bézier曲线的构造,当时是给定节点序列
组合三次Bézier曲线的构造,当时是给定节点序列 和控制顶点
和控制顶点 ,其构造过程是利用
,其构造过程是利用 连续条件,由控制顶点
连续条件,由控制顶点 求出内Bézier点
求出内Bézier点 :
:

然后,由 连续条件求出连接点
连续条件求出连接点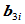 :
:

与此类似,为了构造 组合三次Bézier曲线,我们这里亦基于给定的节点序列
组合三次Bézier曲线,我们这里亦基于给定的节点序列 和控制顶点
和控制顶点 ,利用
,利用 连续性条件求出组合三次Bézier曲线所需要的Bézier点。特别,
连续性条件求出组合三次Bézier曲线所需要的Bézier点。特别, 组合三次Bézier曲线的构造要比
组合三次Bézier曲线的构造要比 组合三次Bézier曲线的构造条件弱,设计者无需预先给定节点序列
组合三次Bézier曲线的构造条件弱,设计者无需预先给定节点序列 ,它可由构造过程自动选取。
,它可由构造过程自动选取。
⑴ 开曲线的构造
Step1.  ;
;
Step2. 在边 上任意选择一点
上任意选择一点 ,在边
,在边 上任意选择一点
上任意选择一点 ;
;
Step3. 在边 ,上任意选择两点
,上任意选择两点 ;
;
Step4. 由 连续条件:
连续条件:

确定节点:

其中 。
。
Step5.  连续条件确定连接点:
连续条件确定连接点:

⑵ 闭曲线的构造
关于闭曲线其构造过程与上述算法的区别是无需Step1和 Step2,Step3的计算对 进行。
进行。
在交互设计过程中, 组合三次Bézier曲线的使用分为两步:①
按上述方法构造的
组合三次Bézier曲线的使用分为两步:①
按上述方法构造的 控制多边形作为曲线的草图;②
调整内Bézier点来精化曲线设计。
控制多边形作为曲线的草图;②
调整内Bézier点来精化曲线设计。
值得注意的是, 组合三次Bézier曲线与
组合三次Bézier曲线与 组合三次Bézier曲线之间的差异。对于
组合三次Bézier曲线之间的差异。对于 组合三次Bézier曲线来说,每一条
组合三次Bézier曲线来说,每一条 组合三次Bézier曲线都具有一个B样条控制多边形,而
组合三次Bézier曲线都具有一个B样条控制多边形,而 组合三次Bézier曲线并非都具有
组合三次Bézier曲线并非都具有 控制多边形。
控制多边形。
Gamma样条曲线
根据 组合三次Bézier曲线的构造可知,两段三次Bézier曲线在公共连接点
组合三次Bézier曲线的构造可知,两段三次Bézier曲线在公共连接点 处关于整体参数
处关于整体参数 连续,则一定存在辅助顶点
连续,则一定存在辅助顶点 ,使得:
,使得:

如果按照此比例得到不重合的两个辅助顶点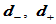 ,则它们将仅仅是
,则它们将仅仅是 连续的,不可能
连续的,不可能 连续,然而可能是
连续,然而可能是 连续。为此,引入以下记号:
连续。为此,引入以下记号:

若要求两段曲线在 处
处 连续,那么由
连续,那么由 连续条件(9.5.3),我们有:
连续条件(9.5.3),我们有:

设 是分别通过
是分别通过 和
和 的两直线之交点,令:
的两直线之交点,令:
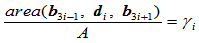
则有:
 (9.6.1)
(9.6.1)
当满足这一组比例关系时, 连续的两段Bézier曲线在公共连接点
连续的两段Bézier曲线在公共连接点 处
处 连续。
连续。
基于这一条件构造的 组合三次Bézier曲线称之为Gamma样条连续,它是由Boehm于1987年提出的,揭示了
组合三次Bézier曲线称之为Gamma样条连续,它是由Boehm于1987年提出的,揭示了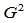 样条曲线和经典B样条曲线之间的本质联系。
样条曲线和经典B样条曲线之间的本质联系。
给定控制顶点 ,节点序列
,节点序列 及形状参数
及形状参数 ,Gamma样条曲线的构造过程如下:
,Gamma样条曲线的构造过程如下:
Step1.  ;
;
Step2.  ;
;
Step3. 在边 ,按照比例关系
,按照比例关系 确定内Bézier点
确定内Bézier点 ,
, :
:

其中, ;
;
Step4. 由 连续条件确定连接点
连续条件确定连接点 :
:

由此得到一条由 ,节点序列
,节点序列 及形状参数
及形状参数 定义的
定义的 组合三次Bézier曲线,它由
组合三次Bézier曲线,它由 段三次Bézier曲线构成。
段三次Bézier曲线构成。
当所有 时,Gamma样条退化为
时,Gamma样条退化为 三次样条曲线;当
三次样条曲线;当 取负值时,曲线上将出现环,曲线亦不再具有凸包性。通常,
取负值时,曲线上将出现环,曲线亦不再具有凸包性。通常, 的取值范围是
的取值范围是 ;当
;当 时,公共连接点
时,公共连接点 及其曲线段被拉向顶点
及其曲线段被拉向顶点 ;当
;当 时,由
时,由 定义的那段曲线被拉成连接
定义的那段曲线被拉成连接 和
和 的直线。因此,
的直线。因此, 可看作是对应于顶点
可看作是对应于顶点
 处的张力参数。
处的张力参数。
在用Gamma样条进行曲线设计时,通常采用以下的设计方法:由设计人员指定一控制多边形,并在除去首末各两条边的剩余每一条边上指定一对不重合的点,作为内Bézier点,由系统自动算出所需要的形状参数、参数节点序列及连接点。
Gamma样条曲线与Nu样条曲线都是 三次样条曲线,且对整体参数
三次样条曲线,且对整体参数 而言均为
而言均为 连续。因此,Gamma样条曲线中的形状参数
连续。因此,Gamma样条曲线中的形状参数 与Nu样条曲线中的形状参数
与Nu样条曲线中的形状参数 应有何种对应关系呢?对此问题的回答,我们留在下节讨论。
应有何种对应关系呢?对此问题的回答,我们留在下节讨论。
