随机向量的定义:
随机试验的样本空间为S={w},若随机变量X1(w),X2(w),…,Xn(w)定义在S上,则称(X1(w),X2(w),…,Xn(w))为n维随机变量(向量)。简记为(X1,X2,…,Xn)。
二维随机向量(X,Y),它可看作平面上的随机点。
对(X,Y)研究的问题:
1.(X,Y)视为平面上的随机点。研究其概率分布——联合分布率、联合分布函数、联合概率密度;Joint
2.分别研究各个分量X,Y的概率分布——边缘(际)分布律、边缘分布函数、边缘概率密度;
marginal
3.X与Y的相互关系;
4.(X,Y)函数的分布。
§ 3.1 二维随机变量的分布
一.离散型随机变量
1.联合分布律
定义3.1 若二维随机变量(X,Y)可能取的值(向量)是有限多个或可列无穷多个,则称(X,Y) 为二维离散型随机变量。
设二维离散型随机变量(X,Y)可能取的值(xi,yj), i,j=1,2…,取这些值的概率为
pij=P{(X,Y)=(xi,yi)}=p{X=xi,Y=yi}i,j=1,2,…
——(3.1)
称 (3.1)式为(X,Y)的联合分布律。
(X,Y)的联合分布律可以用表格的形式表示如下:
|
Y X |
y1 y2 … yj … |
X的边缘分布率 |
|
X1 |
p11 p12 p1j … |
P1·. |
|
X2 |
p21 p22 p2j … |
P2· |
|
M |
M M M |
M |
|
xi |
pi1 pi2 pij … |
Pi· |
|
M |
M M M |
M |
|
Y的边缘分布率 |
P·1 p·2 M p·j … |
1 |
性质:
(1) pij ³ 0,i, j=1,2,…
(2)  =1
=1
2.边缘分布律
设二维离散型随机变量(X,Y) 的联合分布律为
pij= P{X=xi,Y=yi} i, j=1,2,…
分量X和Y的分布律分别为
pi.=P{X=xi} i=1,2,… 满足①pi.³0②S pi.=1
p.j= p{Y=yi}j=1,2,… ①p.j³0②S p.j=1
我们称pi.和p.j分别为(X,Y)关于X和Y的边缘分布律,简称为(X,Y)的边缘分布律。
二维离散型随机变量(X,Y) 的联合分布律与边缘分布率有如下关系:
pi.=P{X=xi}=P{X=xi, S}=P{X=xi,
 (Y=yj)} =
(Y=yj)} =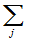 P{X=xi,Y=yj}=
P{X=xi,Y=yj}= pij (3.4)
pij (3.4)
同理可得
p.j = pij (3.5)
pij (3.5)
例1:一整数X随机地在1,2,3三个整数中任取一值,另一个整数Y随机地在1到X中取一值。试求(X,Y)的联合分布率及边缘分布率。
解:
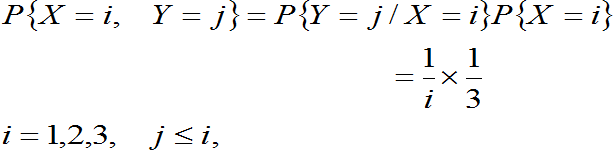
|
Y X |
1 |
2 |
3 |
X的边缘分布率 |
||||
|
1 |
1/3 |
0 |
0 |
1/3 |
p1· |
|||
|
2 |
1/6 |
1/6 |
0 |
1/3 |
p2· |
|||
|
3 |
1/9 |
1/9 |
1/9 |
1/3 |
p3· |
|||
|
Y的边缘分布率 |
11/18 |
5/18 |
1/9 |
1 |
||||
|
P·1 |
p·2 |
p·3 |
||||||
二.联合分布函数与边缘分布函数
1.定义3.2 设(X,Y)是二维随机变量,对任意的实数x,y令
F(x,y)=P{X£x,Y£y} (3.7)
则称 F(x,y)为(X,Y)的联合分布函数。

2.F(x,y)的性质:
性质1 对于x和y,F(x,y)都是单调不减函数,即若x1<x2,对任意的实数y,则有 F(x1,y)£F(x2,y);
若y1<y2,对任意的实数x,则有 F(x,y1)£F(x,y2)。
性质2 对于任意的实数x,y,均有
0£F(x,y)£1, 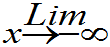 F(x,y)=0,
F(x,y)=0,
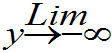 F(x,y)=0,
F(x,y)=0,  F(x,y)=1。
F(x,y)=1。
性质3 对于x和y,F(x,y)都是右连续的,即对任意的实数x0和y0,均有
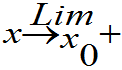 F(x,y)=F(x0,y),
F(x,y)=F(x0,y),
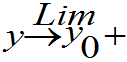 F(x,y)=F(x,y0)。
F(x,y)=F(x,y0)。
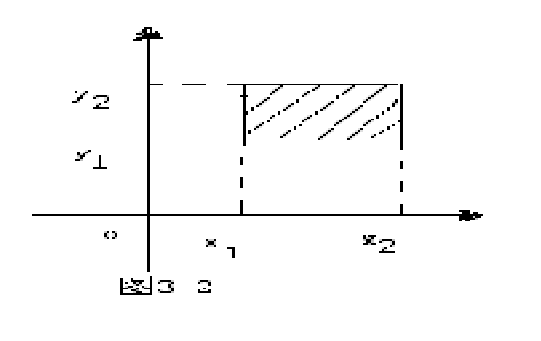
性质4 若x1<x2, y1<y2, 则
F(x2,,y2)-F(x2,y1) -F(x1,y2)+F(x1,y1)³0
(X,Y)落于下图阴影部分的矩形区域内的概率为:
F(x2,,y2)-F(x2,y1)-F(x1,y2)+F(x1,y1)
=P{x1<X£x2,y1<Y£y2}
例 2 P71,
照书上讲。
3.边缘分布
(X,Y)的分量X,Y的分布函数分别为FX(x)和FY(y),称它们为X,Y的边缘分布函数。它们与F(x,y)的关系如下:
FX(x)=P{X£x}=P{X£x,-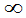 <Y<+
<Y<+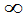 }=F(x,+
}=F(x,+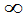 ),
),
FY(y)=P{Y£y}=P{-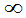 <X<+
<X<+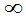 ,Y£y}=F(+
,Y£y}=F(+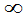 ,y)。
,y)。
例2:(第一版)设
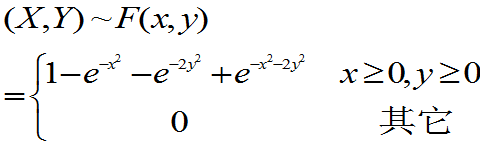 ,
,
求:(1) (X,Y)的边缘分布函数;
(2)P(1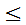 x
x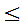 2,-1
2,-1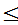 y
y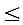 3)。
3)。
(3)P(X>2,Y>3)= 1- P(X
1- P(X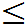 2,Y
2,Y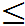 3)
3) ?
?
