第三讲 线性变换及其矩阵
一、线性变换及其运算
定义:设V是数域K上的线性空间,T是V到自身的一个映射,使得对于V中的任意元素x均存在唯一的y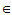 V与之对应,则称T为V的一个变换或算子,记为
V与之对应,则称T为V的一个变换或算子,记为
Tx=y
称y为x在变换T下的象,x为y的原象。
若变化T还满足
T(kx+ly)=k(Tx)+l(Ty)
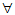 x,y
x,y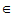 V, k,l
V, k,l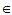 K
K
称T为线性变换。
[例1] 二维实向量空间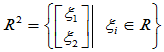 ,将其绕原点旋转
,将其绕原点旋转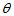 角的操作就是一个线性变换。
角的操作就是一个线性变换。
[证明] 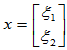
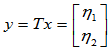
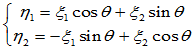
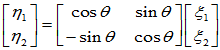
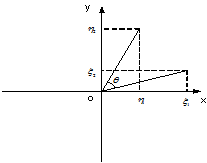
可见该操作T为变换,下面证明其为线性变换
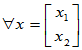
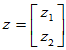
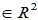 ,k,l
,k,l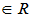
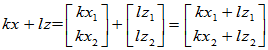
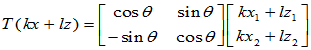
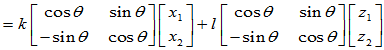
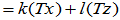
 T是线性变换。
T是线性变换。
[例2] 次数不超过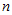 的全体实多项式
的全体实多项式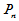 构成实数域上的一个
构成实数域上的一个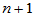 维的线性空间,其基可选为
维的线性空间,其基可选为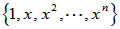 ,微分算子
,微分算子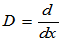 是
是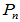 上的一个线性变换。
上的一个线性变换。
[证明] 显然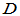 对
对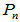 而言是变换,
而言是变换,
要证明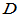 满足线性变换的条件
满足线性变换的条件
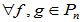 ,k,l
,k,l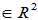
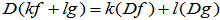
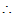
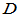 是
是 上的线性变换。
上的线性变换。
2. 性质
- 线性变换把零元素仍变为零元素
- 负元素的象为原来元素的象的负元素
- 线性变换把线性相关的元素组仍变为线性相关的元素组
[证明] 线性变换T(kx+ly)=k(Tx)+l(Ty)
(1)T(0)=T(0x)=0(Tx)=0
(2)T(-x)=(-1)(Tx)=-(Tx)
(3)元素组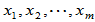 线性相关,即存在一组不全为零的数
线性相关,即存在一组不全为零的数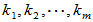 使
使
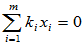
则 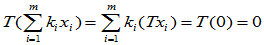
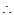
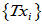 线性相关。
线性相关。
[得证]
应该注意,线性无关的元素组经过线性变换不一定再是线性无关的,变换后的情况与元素组和线性变换有关。若线性变换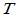 将所有的元素组仍变换为线性无关的元素组,则称之为满秩的线性变换,其变换矩阵为满秩矩阵。
将所有的元素组仍变换为线性无关的元素组,则称之为满秩的线性变换,其变换矩阵为满秩矩阵。
3. 线性变换的运算
- 恒等变换
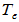 :
: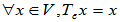
- 零变换
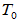 :
: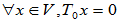
- 变换的相等:
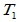 、
、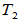 是
是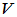 的两个线性变换,
的两个线性变换,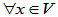 ,均有
,均有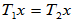 ,则称
,则称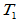 =
=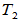
- 线性变换的和
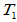 +
+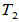 :
: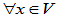 ,
,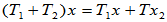
- 线性变换的数乘
 :
: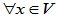 ,
,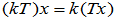
负变换:
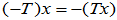
- 线性变换的乘积
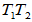 :
: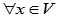 ,
,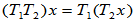
- 逆变换
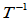 :
: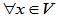 ,若存在线性变换
,若存在线性变换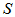 使得
使得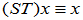 ,则称
,则称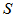 为
为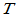 的逆变换
的逆变换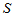 =
=
- 线性变换的多项式:
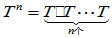 ,并规定
,并规定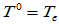
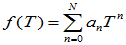
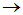

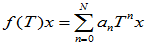
需要说明的是:
1)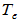 也称为单位变换,它的矩阵表示为单位矩阵
也称为单位变换,它的矩阵表示为单位矩阵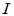 ;
;
2)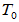 对应的矩阵表示为零矩阵;
对应的矩阵表示为零矩阵;
3)和矩阵的乘积一样,线性变换的乘积不满足交换律;
4)不是所有的变换都具有逆变换,只有满秩变换才有逆变换,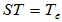 ;
;
5)恒等变换、零变换、线性变换的和、乘积多项式及逆变换(若存在)均为线性变换。
二、线性变换的矩阵表示
线性变换用矩阵表示,将抽象的线性变换转化为具体的矩阵形式。
设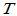 是线性空间
是线性空间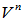 的一个线性变换,且
的一个线性变换,且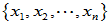 是
是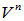 的一个基,
的一个基,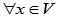 n,存在唯一的坐标表示
n,存在唯一的坐标表示
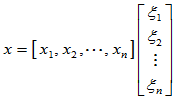 =
=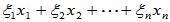
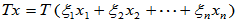
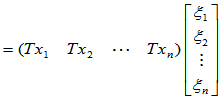
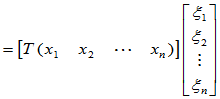
因此,要确定线性变换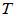 ,只需确定基元素在该变换下的象就可以了。
,只需确定基元素在该变换下的象就可以了。
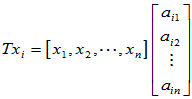
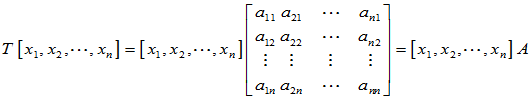
对于任意元素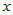 ,在该基下,变换后
,在该基下,变换后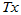 的坐标表示为
的坐标表示为
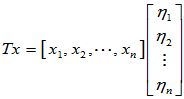
同时
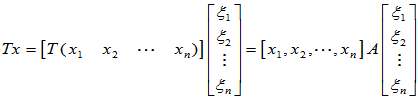
对比可知:
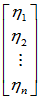 =
=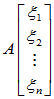
即: 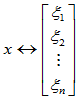
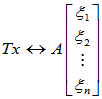
- 定义:把
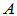 称为
称为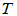 在基
在基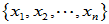 下的矩阵。
下的矩阵。
- 定理:设
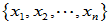 是
是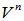 的一个基,
的一个基,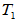 、
、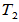 在该基下的矩阵分别为
在该基下的矩阵分别为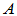 、
、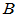 。则有
。则有
(1)
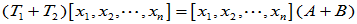
(2)
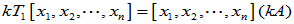
(3)
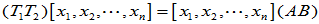
(4)
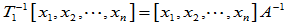
推论1. 设
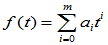 为纯量t的m次多项式,
为纯量t的m次多项式,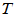 为线性空间
为线性空间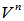 的一个线性变换,且在
的一个线性变换,且在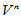 的基
的基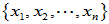 下的矩阵为
下的矩阵为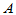 ,则
,则
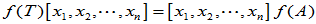
其中
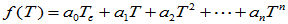
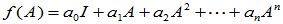
推论2. 设线性变换
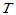 在
在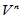 的基
的基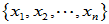 下的矩阵为
下的矩阵为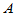 ,元素
,元素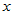 在该基下的坐标为
在该基下的坐标为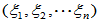 ,则
,则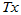 在该基下的坐标
在该基下的坐标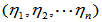 满足
满足
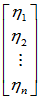 =
=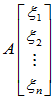
3.相似矩阵
设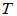 在
在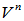 的两个基
的两个基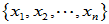 及
及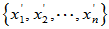 的矩阵分别为
的矩阵分别为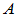 和
和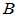 ,且
,且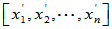 =
=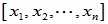
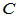 ,则
,则
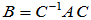
即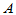 和
和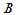 为相似矩阵。
为相似矩阵。
[证明] 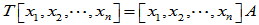
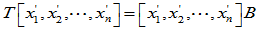
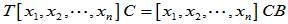
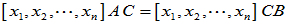
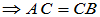 即
即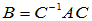
定理: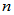 阶方阵
阶方阵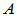 和
和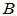 相似的充要条件是
相似的充要条件是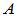 和
和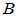 为同一线性变换在不同基下的矩阵。
为同一线性变换在不同基下的矩阵。
[证明] 必要性:已知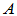 和
和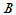 相似,即存在可逆矩阵
相似,即存在可逆矩阵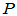 使
使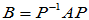
选取一个基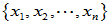 ,定义
,定义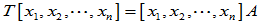
考虑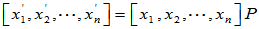 可作为基,且
可作为基,且
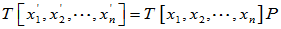
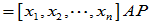
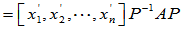
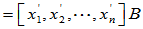
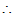
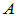 和
和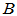 为同一线性变换在不同基下的矩阵。
为同一线性变换在不同基下的矩阵。
充分性的证明由相似矩阵定义的证明给出。
三、线性变换及矩阵的值域和核
- 定义:设
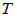 是线性空间
是线性空间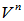 的线性变换,称
的线性变换,称
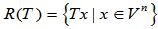 为
为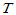 的值域;
的值域;
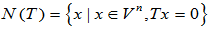 称为
称为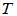 的核。
的核。
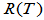 和
和 均为
均为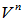 的子空间。
的子空间。
设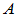 为
为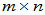 阶矩阵,称
阶矩阵,称
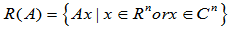 为矩阵
为矩阵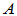 的值域;
的值域;
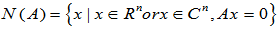 为
为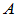 的核。
的核。
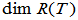 、
、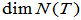 称为
称为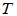 的秩和零度;
的秩和零度;
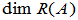 、
、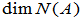 称为
称为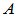 的秩和零度。
的秩和零度。
- 定理:(1)
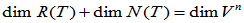
(2)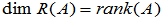
(3)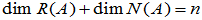 ,
,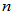 为
为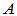 的列数。
的列数。
若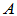 是线性变换
是线性变换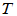 的矩阵,则
的矩阵,则
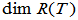 =
=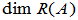 ,
,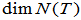 =
=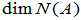
作业:P77-78,1、26、7
