§1 复元素的引进,二次曲线与直线的交点
一 平面上的复元素
设在平面上建立了一个直角坐标系{O;i,j},今将平面上点的概念扩充如下:任意一对有序复数(x,y)都是平面上一点p的坐标,若x,y全为实数,则称p为实点,否则称p为虚点,实点和虚点统称为复点。点的概念扩充以后,原来的实平面即变为复平面。
今在复平面上引入下列复元素:
(1)复矢量:以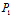 (
( ,
,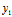 )为始点,
)为始点,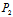 (
(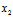 ,
,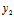 )为终点的复矢量定义为:
)为终点的复矢量定义为:
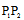 =(
=(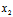 -
-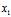 )i+(
)i+( -
- )j,其中
)j,其中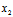 -
-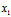 ,
,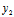 -
-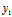 称为它的分量,记作
称为它的分量,记作
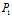
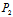 {
{ -
-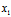 ,
,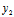 -
- },分量不全为实数的矢量称为虚矢量,否则称为实矢量;若二矢量的对应分量成比例,则称这二矢量是平行的。
},分量不全为实数的矢量称为虚矢量,否则称为实矢量;若二矢量的对应分量成比例,则称这二矢量是平行的。
(2)复直线:在直角系下,一次方程
ax+by+c=0 (a,b为复数)
所表示的图形,称为复直线;若a,b,c与三实数对应成比例,则称其为实直线,否则称其为虚直线。 注意:实直线可以有虚点。
注:实直线上有无穷多个复点,但虚直线上只有一个实点。
(3)定此分点:
设有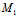 (
( ,
,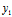 ),
),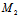 (
(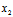 ,
,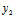 ),若点M(x,y)的坐标满点
),若点M(x,y)的坐标满点
x=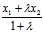 , y=
, y=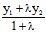 (λ≠-1)
(λ≠-1)
则称M为线段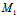
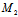 的定比分点,λ——定比,特别地,
的定比分点,λ——定比,特别地,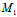
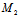 的中点为(
的中点为(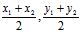 )
)
(4)共轭复元素:
若 与
与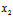 ,
,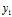 与
与 分别为共轭复数,则称P(
分别为共轭复数,则称P(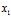 ,
,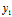 )与
)与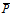 (
(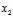 ,
,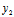 )为一对共轭复点。显然实点与其自身共轭;二共轭复点连接线段的中点为实点。若二直线
)为一对共轭复点。显然实点与其自身共轭;二共轭复点连接线段的中点为实点。若二直线
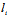 :
: x+
x+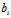 y+
y+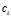 =0,i=1,2满足
=0,i=1,2满足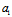 与
与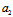 共轭,
共轭,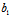 与
与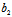 共轭,
共轭,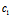 与
与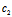 共轭,则称
共轭,则称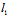 与
与 是一对共轭复直线,若二矢量的对应分量为共轭复数,则称这二矢量为共轭复矢量。
是一对共轭复直线,若二矢量的对应分量为共轭复数,则称这二矢量为共轭复矢量。
注:在复平面上无法推广实平面上的距离公式,这是因为,在实平面上
d²=(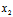 -
-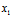 )²+(
)²+( -
-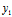 )²
)²
而在复平面上,上式右端为一复数,其平方根有两个地位均等的值,无法确定其中一个为二点间的距离。
二 二次曲线与与(实)直线的交点:
设有二次曲线 C:F(x,y)≡ x²+2
x²+2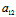 xy+
xy+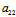 y²+2
y²+2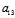 x+2
x+2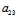 y+
y+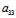 =0 及直线
=0 及直线
l:
为研究l与c的交点情况,另需研究满足下述方程的t的取值情况
(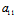 X²+2
X²+2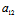 XY+
XY+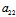 Y²)t²+2{(
Y²)t²+2{(
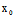 +
+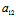
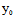 +
+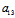 )X+(
)X+(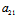
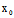 +
+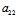
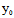 +
+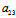 )Y}
)Y}
+F(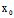 ,
, )=0
)=0
即Φ(X,Y)t²+2[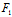 (
(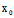 ,
,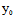 )X+
)X+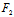 (
( ,
, )Y]t+F(
)Y]t+F( ,
,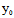 )=0 (*)
)=0 (*)
(1)若Φ(X,Y)≠0
(*)的判别式
△=4{[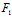 (
(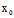 ,
, )X+
)X+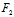 (
(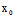 ,
,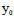 )Y]²-Φ(X,Y)F(
)Y]²-Φ(X,Y)F(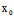 ,
,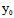 )}
)}
当△>0时,l与C交于二不同实点;
当△<0时,l与C交于二不同虚点;
当△=0时,l与C交于二重合实点——相切
(ii )若Φ(X,Y)=0
当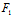 (
(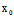 ,
,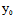 )X+
)X+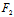 (
(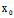 ,
,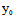 )Y≠0时,(*)有一实根,从而C与l仅交于一个实点(并非相切)
)Y≠0时,(*)有一实根,从而C与l仅交于一个实点(并非相切)
当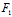 (
(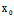 ,
,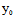 )X+
)X+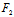 (
( ,
, )Y=0,但F(
)Y=0,但F(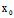 ,
,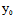 )≠0时,(*)为矛盾方程
)≠0时,(*)为矛盾方程
∴C与l不交
当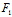 (
(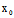 ,
,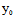 )X+
)X+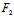 (
(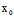 ,
,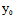 )Y=F(
)Y=F(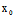 ,
,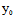 )=0时,(*)为恒等式
)=0时,(*)为恒等式
∴l在二次曲线C上——相切
