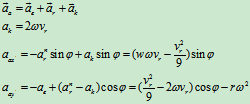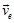第九章点的复合运动
教学目标
1 深刻理解三种运动、三种速度和三种加速度的定义,运动的合成与分解以及运动相对性的概念。
2 对具体问题能恰当地选择动点、动系和定系,进行运动轨迹、速度和加速度分析。并能正确计算科氏加速度的大小并确定它的方向。
3 会推导速度合成定理、牵连运动为平动时点的加速度合成定理,弄懂牵连运动为转动时的加速度合成定理。并能熟练地应用上述三个定理。
本章重点
运动的合成与分解,速度合成定理及加速度合成定理及其应用。
本章难点
牵连点、牵连速度、牵连加速度及科氏加速度的概念,动点、动系的选择和相对运动的分析。
教学过程
- 三种运动的概念
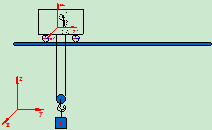
动点:M
动系:车
静系:地面(地球)
绝对运动:动点相对于静系的运动。运动主体是动点。
相对运动:动点相对于动系的运动。
牵连运动:动系相对于静系的运动。运动主体是动系。
例1当自行车沿直线行驶时,以地面为静系,车架为动系,观察脚蹬的运动。
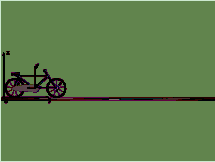

例2 当直升飞机直上天空时,
以地面为静系,飞机机身为动系,观察直升飞机螺旋桨
上叶片端点上的一点的运动。
- 速度合成定理
- 三种速度的概念
绝对速度
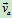 :动点相对于静系的速度。
:动点相对于静系的速度。
相对速度
 :动点相对于动系的速度。
:动点相对于动系的速度。
牵连速度
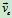 :牵连点相对于静系的速度。
:牵连点相对于静系的速度。
牵连点:某瞬时动系上与动点相重合的那一点称为动
点的牵连点。
牵连点举例之一:
狗熊在车上行走。
牵连点举例之二:
蜗牛沿转动杆爬行。
- 速度合成定理
绝对位移
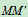
相对位移

牵连位移:
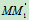

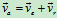
- 在凸轮顶杆机构中已知凸轮以速度
 直线平动,已知半径为
直线平动,已知半径为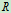 ,求图示
,求图示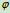 角时顶杆AB的速度。
角时顶杆AB的速度。
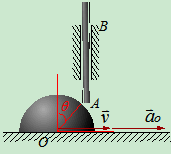
解:
1 选动点、动系:动点A,动系凸轮。
2 三种运动分析:
绝对运动:直线
相对运动:圆周运动
牵连运动:直线平动
3 速度分析: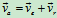
4 求解: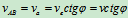
思考:如选AB杆为动系,凸轮上的点为动点,怎样分析?
例2 曲柄摇杆机构,设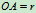 ,以匀角速度
,以匀角速度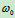 转动图中
转动图中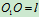 。求
。求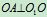 时,摇杆
时,摇杆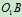 的角速度。
的角速度。

解:1 选动点、动系:动点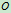 ,动系
,动系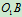 。
。
2 三种运动分析:
绝对运动:圆周运动直线
相对运动:直线
牵连运动:圆周运动
3 速度分析: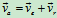
4 求解:
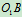

思考:如选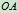 杆为动系,
杆为动系, 上的点为动点,怎样分析?
上的点为动点,怎样分析?
例3:半径为R,偏心距OC= 的轮C以
的轮C以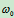 绕转轴O匀速转动,从而推动
绕转轴O匀速转动,从而推动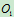 轴转动当OC在同一铅直线上时
轴转动当OC在同一铅直线上时 =
= 时,试求该
时,试求该 杆的角速度。
杆的角速度。
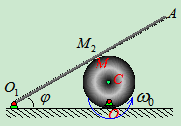
解:分析:设 、
、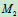 分别为轮与杆的接触点。选
分别为轮与杆的接触点。选 为动点,
为动点,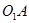 为动系,相对运动为未知曲线(让机构运动画出其相对轨迹);选
为动系,相对运动为未知曲线(让机构运动画出其相对轨迹);选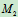 点为动点,轮C为动系相对运动也为未知曲线(让机构运动画出相对轨迹)
点为动点,轮C为动系相对运动也为未知曲线(让机构运动画出相对轨迹)
- 选C点为到点,动系为
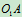 杆
杆
- 分析运动:绝对运动:以O为圆心OC长为半径的圆。
牵连运动:定轴转动
相对运动:平行于 直线
直线
- 速度分析:

|
|
| |
方向 |
|
| // |
大小 |
|
| 未知 |
- 求解:
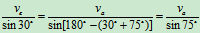
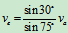
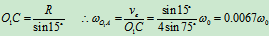
(思考题:为什么例1、例2能选接触点为动点进行分析,而本题不能选接触点为动点进行分析?)
例4、直线AB以大小为 的速度沿垂直于AB的方向向上移动,而直线CD以大小为
的速度沿垂直于AB的方向向上移动,而直线CD以大小为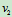 的速度沿垂直于CD的方向向左上方移动,如图所示。设两直线间的夹角为
的速度沿垂直于CD的方向向左上方移动,如图所示。设两直线间的夹角为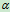 ,试求两直线的交点M的速度。
,试求两直线的交点M的速度。
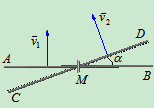
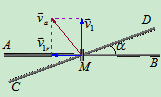

解:在M点设一小环,套着两杆,两杆交点的速度,即为小环M的速度。
1、动点:M 动系:AB
2、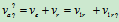
3、有3 个未知量,求不出。
2、动点:M动系CD
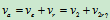 (B)
(B)
联立式(A)和(B)有

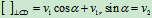
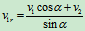

例5、车A沿半径R=150cm的圆弧道路以速度 km/h行驶,车B沿直线道路以速度
km/h行驶,车B沿直线道路以速度 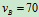 km/h匀速行驶,运动至图9.30所示位置时A、B两车相距100m。试求(1)A车相对B车的速度。(2)B车相对A车的速度。
km/h匀速行驶,运动至图9.30所示位置时A、B两车相距100m。试求(1)A车相对B车的速度。(2)B车相对A车的速度。
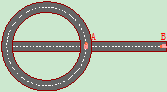

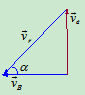
解:(1)求A车相对B车的速度
选动点A车动系B车
牵连运动:随B车平动
绝对运动:圆运动
相对运动:未知

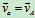 ,
,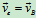

其大小为
与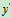 轴夹角
轴夹角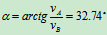
(2)求B车相对A车的速度选动点B车,动系A车
牵连运动:绕圆弧道路的圆心O的定轴转动,转动角速度
绝对运动:直线运动;
相对运动:未知;
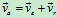
其中 ,
,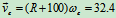 m/s
m/s
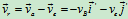
其大小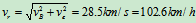
与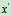 轴夹角
轴夹角
如图9.3c所示
- 加速度合成定理
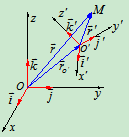
1、速度的概念
绝对加速度:动点相对静系的加速度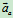
牵连加速度:牵连点相对静系的加速度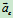
相对加速度:动点相对动系的加速度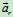
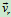 、
、 的坐标表示:
的坐标表示:
相对运动方程: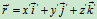
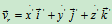

2、运动为平动时加速度合成定理
在图9.4中设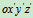 为平动坐标系,则
为平动坐标系,则 、
、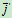 、
、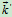 的大小,方向均不变,是常矢量
的大小,方向均不变,是常矢量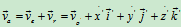 (a)
(a)
在静系中,将式(a)对时间t求一阶导数,有:

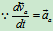 ,
, ,
,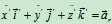
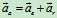
3、牵连运动为转动时合成定理
为方便,可将动系 的坐标原点选在转轴上,即在图9.4中设
的坐标原点选在转轴上,即在图9.4中设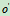 点不动,此时牵连速度、牵连加速度可表示为:
点不动,此时牵连速度、牵连加速度可表示为:
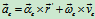
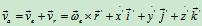
在静系中,将式(b)对时间t求一阶导数,有:

在图中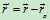 ,
,  是常矢量,有
是常矢量,有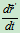 =
=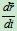 =
= =
=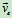 +
+
由泊桑公式: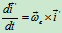

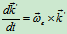
式(c)的最后三项可表示为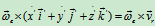
将式(d)(e)代入式(c),有: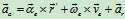
其中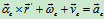
令 称为哥氏加速度
称为哥氏加速度
所以牵连运动为转动时的加速度合成定理为
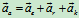
4、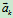 的计算及产生的原因分析:
的计算及产生的原因分析:
参看图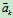 =
=
当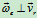 时有
时有 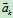 =
= 时。
时。
产生的原因分析:
设动点M沿直杆OA的速度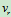 匀速运动,而杆又以
匀速运动,而杆又以 匀速转动,如图所示。
匀速转动,如图所示。
在静系中观察, 的方向发生了改变,其中变化率
的方向发生了改变,其中变化率

方向垂直与OA杆,
产生原因:由于牵连运动改变了 的方向所致。当M点运动到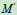 位置的时候时,牵连速度的大小发生了变化,其变化率为
位置的时候时,牵连速度的大小发生了变化,其变化率为
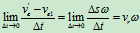
方向垂直于OA杆
产生原因:由于相对运动改变了牵连点,改变了牵连点,牵连速度的大小而所致。
总之是由于牵连运动和相对运动的相互影响而造成的。
用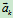 说明地球上的一些自然现象。
说明地球上的一些自然现象。
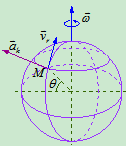
例如:在北半球,沿经线流动的江河,若顺着河水流动的方向看,河的左半岸被冲刷得较为厉害。这时因为:选河水为动点,地球为动系,地心系(地球中心为坐标原点,三个坐标轴指向三颗恒星)为静系。若设河水向北流,如图9。7
则河水的哥氏加速度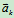 指向左侧(如图),有动力学知,河的右岸对水作用了向
指向左侧(如图),有动力学知,河的右岸对水作用了向
左的力。根据作用于反作用定律,河水对右岸必作用反力,因而右岸被左岸冲刷厉
害。在北纬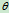 角位置。河水的哥氏加速度为
角位置。河水的哥氏加速度为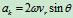 (
( 地球
地球
的角速度)由此可知:沿经线运动时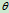 =0(赤道上)
=0(赤道上)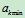 =0,
=0,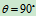 北极(南极)
北极(南极) 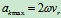
例6曲线OA绕固定轴O转动,丁字形杆BC沿水平方向往复平动,如图9.8所示。铰接在曲柄端A的滑块,可在丁字形的铅直槽DE内滑动。设曲柄的转动规律为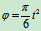 ,OA=r,试求t=1s时,杆BC的加速度。
,OA=r,试求t=1s时,杆BC的加速度。

解:1、动点A动系BC杆。
分析运动:
绝对运动:A点作圆运动,OA杆作定轴转动。
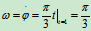
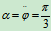

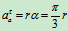 ,
,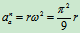
牵连运动水平直线平动
相对运动沿DE直线运动
2、加速度分析
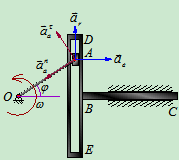


例7:(在例1中的已知条件中,若已知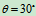 凸轮的加速度为
凸轮的加速度为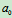 方向如图9.9所示,试求AB杆的加速度
方向如图9.9所示,试求AB杆的加速度
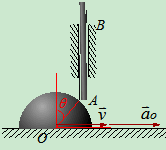
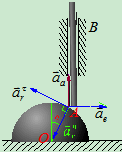
解:在例1中已选动点A,动系凸轮可求得: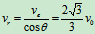
加速度分析:
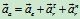
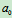

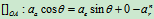
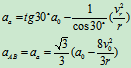
例8:在例2中求图示瞬时 杆的角速度
杆的角速度

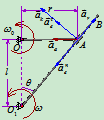
解:在例2中选动点A,动系 杆则动系为转动,相对运动为直线求得
杆则动系为转动,相对运动为直线求得 杆角速度
杆角速度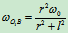 和相对速度
和相对速度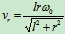
加速度分析: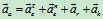 (方向如图9.10)
(方向如图9.10)

其中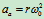 ,
, 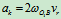
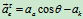 ,
, 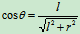
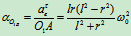
例9:空气压缩机的工作轮以角速度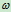 绕垂直于图面的O轴匀速转动,空气以相对速度
绕垂直于图面的O轴匀速转动,空气以相对速度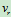 沿弯曲的叶片匀速流动,如图9.11所示,如曲线AB在C点的曲率半径为9,通过点C的法线与半径间所夹的角为
沿弯曲的叶片匀速流动,如图9.11所示,如曲线AB在C点的曲率半径为9,通过点C的法线与半径间所夹的角为 ,CO=r,求气体微团在点C的绝对加速度
,CO=r,求气体微团在点C的绝对加速度
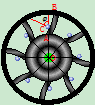

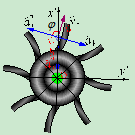
解:1、选动点:微团气体C,动系:工作轮
2、分析运动:
牵连运动:定轴转动: ,
,
相对运动:匀速曲线运动: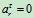 ,
,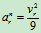
绝对运动:未知。
3、加速度分析: