第五章摩擦平衡问题
教学目标
1 能区分滑动摩擦力与极限滑动摩擦力。对滑动摩擦定律有清晰的理解。
2 能熟练计算考虑摩擦力的物体的平衡问题。
3 理解摩擦角的概念和自锁现象,能用摩擦角解物体的平衡问题。
4 理解滚动摩阻定律。学会解滑动摩擦和滚动摩阻同时存在的平衡问题。
本章重点
滑动摩擦力和极限滑动摩擦力,滑动摩擦定律。
考虑摩擦时物体的平衡问题。平衡的临界状态和平衡范围。
本章难点
用摩擦角解物体、物体系的平衡问题。
教学过程
一.1.概念:两个相互接触的物体,当接触面之见有相对滑动或相对滑动趋势时,彼此阻碍滑动的机械作用。
2.滑动摩擦力的性质和库仑摩擦定律
演示
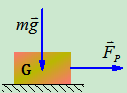
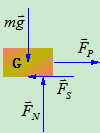
质量为的物体静止地置于水平面上,设两者接触面都是非光滑面。现在物块上施加水平力并令其自零开始增加。
 .静滑动摩擦力的方向与物体相对运动趋势方向相反,大小在零与最大静摩擦力之间,即
.静滑动摩擦力的方向与物体相对运动趋势方向相反,大小在零与最大静摩擦力之间,即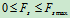 (4-1)
(4-1)
一般静摩擦力又平衡条件确定,最大静摩擦力 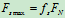
称为库仑摩擦定律,其中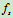 是静摩擦系数。
是静摩擦系数。
 .动滑动摩擦力的方向与相对滑动方向相反,大小
.动滑动摩擦力的方向与相对滑动方向相反,大小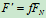 称为库仑动摩擦定律,是动摩擦系数。
称为库仑动摩擦定律,是动摩擦系数。
二.摩擦角与自锁现象
- 摩擦角
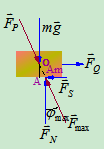
考察图中所示的物体受力,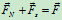 称为全反力,全反力与法向约束力的夹角用
称为全反力,全反力与法向约束力的夹角用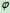 来表示,
来表示,
在保持物块静止的前提下,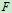 、
、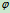 随
随 的增大而增大,当
的增大而增大,当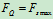 时,
时,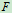 达到最大值,其作用点由
达到最大值,其作用点由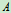 移至
移至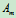 ,这时角度
,这时角度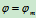 称为摩擦角。一般情形下
称为摩擦角。一般情形下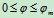
该式表示全约束反力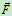 在二维空间的作用范围,(4-2)和(4-4)分别为静滑动摩擦力有最大限定值
在二维空间的作用范围,(4-2)和(4-4)分别为静滑动摩擦力有最大限定值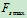 这一概念的解析与几何表达式,因而二者等价。
这一概念的解析与几何表达式,因而二者等价。
当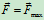 时,有
时,有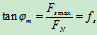
故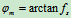 (4-5)
(4-5)
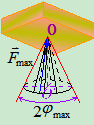
它表明,摩擦角的正切等于静摩擦系数。在图5.3中,若将作用线过点 的力
的力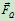 连续改变它在水平面内的方向,则全约束反力
连续改变它在水平面内的方向,则全约束反力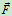 的方向也随之改变。假定两物体接触面沿任意方向的静摩擦系数均相同,这样,在两物体处于领结平衡状态时,全约束力
的方向也随之改变。假定两物体接触面沿任意方向的静摩擦系数均相同,这样,在两物体处于领结平衡状态时,全约束力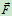 的作用线将再空间形成一个顶角为
的作用线将再空间形成一个顶角为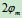 的正圆锥面,称之为摩擦锥。摩擦锥是全约束力
的正圆锥面,称之为摩擦锥。摩擦锥是全约束力 在三维空间内的作用范围。
在三维空间内的作用范围。
- 自锁
如果作用在物体上的全部主动力的合力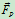 的作用线在摩擦锥之内,则无论这个力怎么大,物体总能保持平衡,这种现象称为摩擦自锁。反之,如果全部主动力的合力的作用线在摩擦锥外,无论这个力怎么小,物体一定不能平衡。
的作用线在摩擦锥之内,则无论这个力怎么大,物体总能保持平衡,这种现象称为摩擦自锁。反之,如果全部主动力的合力的作用线在摩擦锥外,无论这个力怎么小,物体一定不能平衡。
演示:重为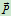 的物体放在斜面上,当斜面倾角
的物体放在斜面上,当斜面倾角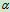 逐渐增大,物体与斜面的摩擦角为
逐渐增大,物体与斜面的摩擦角为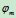 ,物体的运动状态
,物体的运动状态
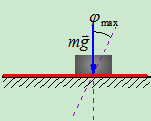
从图中可以看出,  物体保持平衡
物体保持平衡
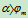 物体发生运动
物体发生运动
 物体处于平衡与运动的临界状态
物体处于平衡与运动的临界状态
由此可知:物体在有摩擦的斜面上的自锁条件是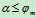
三.考虑摩擦的平衡问题
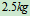 的物体与倾角为
的物体与倾角为 的斜面间的静滑动摩擦系数
的斜面间的静滑动摩擦系数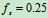 ,求当水平力
,求当水平力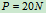 时,摩擦力的大小,方向。
时,摩擦力的大小,方向。

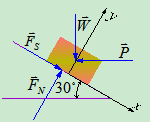
解:
- 取研究对象:物块
- 受力分析:假定物体处于静止状态且有沿斜面向上的运动趋势,所以摩擦力方向如图,其它受力如图。当然也可以假定物体有沿斜面向下运动趋势,于是摩擦力方向与图示相反。
- 列方程求解:

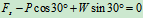
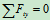
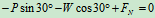
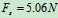
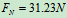
- 检验:

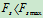
所以物体处于静止状态 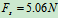
- 在斜面上放一重为
 的物体,已知斜面的倾角
的物体,已知斜面的倾角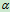 大于摩擦角
大于摩擦角 ,试求维持物体在斜面上静止所需水平力
,试求维持物体在斜面上静止所需水平力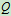 的大小
的大小
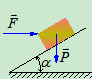
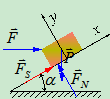
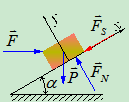
- 解析法
- 取研究对象:物块
- 分析受力:因为
 ,如果没有力作用,物体将沿斜面下滑,故要使物体在斜面上静止,必须有
,如果没有力作用,物体将沿斜面下滑,故要使物体在斜面上静止,必须有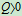 。若力
。若力 较小时,物体有下滑趋势,摩擦力沿斜面向上;反之,若力
较小时,物体有下滑趋势,摩擦力沿斜面向上;反之,若力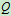 较大时,物体有上滑趋势,摩擦力沿斜面向下。
较大时,物体有上滑趋势,摩擦力沿斜面向下。
- 物体有下滑趋势,受力如图5.7
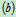
图5.7
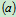
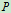

图5.7
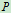
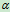
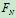

图5.7

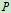
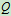
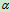
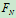
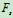
列方程:

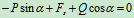
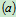
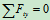
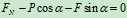

物理条件: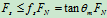

联立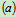
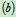
 可得:
可得: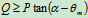
- 物体有下滑趋势,受力如图5.7

列方程 :

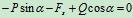
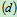

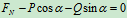
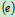
物理条件:
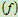
联立

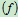 可得:
可得: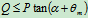
综上所述,物体要在斜面上保持静止,应满足 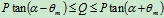
- 几何法
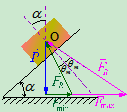
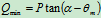
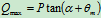

例三.图 所示为攀登电线杆时所采用脚套钩。已知套钩的尺寸
所示为攀登电线杆时所采用脚套钩。已知套钩的尺寸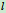 ,电线杆的直径
,电线杆的直径 ,摩擦系数
,摩擦系数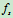 。试求套钩不致下滑时脚踏力
。试求套钩不致下滑时脚踏力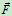 的作用线与电线杆中心线的距离
的作用线与电线杆中心线的距离 。
。
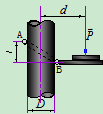


解:
- 解析法:
- 取研究对象:套钩
- 受力分析:如图
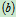
- 列方程
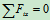
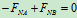
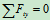
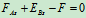
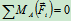
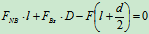
物理条件: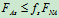

联立以上各式可得:
- 几何法:
分别作出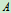 、
、 两处的摩擦角,相应得到两处的全约束反力
两处的摩擦角,相应得到两处的全约束反力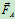 和
和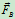 的方向。于是,套钩应在
的方向。于是,套钩应在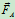 、
、 和
和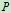 三个力作用下处于临界平衡,故三力必交于一点
三个力作用下处于临界平衡,故三力必交于一点 。
。
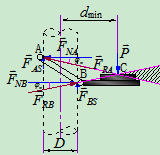


由此解得: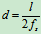 由图可知:
由图可知:
- 滚动摩阻
- 滚动摩阻力偶:滚动摩阻是指一物体沿另一物体表面作相对滚动或有滚动趋势时,接触面间产生的一种阻碍滚动的机械运动。从实例分析,水平面有滚子处于平衡状态,滚子无运动趋势,接触面间无摩擦力。
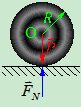
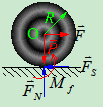
在滚子中心加一较小的力,滚子仍平衡。说明存在摩擦力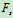 ,由
,由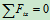 :
: 知
知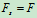 力
力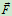 与
与 形成一对力偶,使滚子滚动。由于滚子静止,所以接触面间产生一个阻碍滚子滚动的力偶
形成一对力偶,使滚子滚动。由于滚子静止,所以接触面间产生一个阻碍滚子滚动的力偶 ,该力偶称为滚动摩阻力偶,简称滚阻力偶,它的转向与滚子滚动的趋势相反。
,该力偶称为滚动摩阻力偶,简称滚阻力偶,它的转向与滚子滚动的趋势相反。
- 滚动摩阻力偶的成因:滚子和路面有接触变形
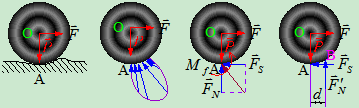
受到较小的水平拉力 ,约束力分布不均匀。
,约束力分布不均匀。
将此分布力系向点简化,得到主矢 和主矩
和主矩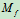 ,此
,此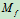 即是滚动摩阻力偶,
即是滚动摩阻力偶,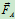 可分解为
可分解为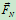 和
和 ,将
,将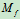 和
和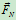 合成为点的一个力,偏离一段微小距离
合成为点的一个力,偏离一段微小距离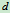 ,
,
当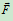 增大,
增大, 增大,滚子处于临界状态时,滚子达到最大偏离量
增大,滚子处于临界状态时,滚子达到最大偏离量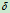 ,这时滚动摩阻力偶也达到最大,可表示为
,这时滚动摩阻力偶也达到最大,可表示为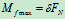 ,
, 称为滚动摩阻系数
称为滚动摩阻系数
一般情况下,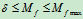
- 滑动摩擦力在滚动运动中的作用
上述分析表明,物体滚动前后,除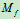 存在外,还存在
存在外,还存在 ,力
,力 阻碍轮与接触面在接触处的相互滑动,但不阻碍滑动,相反还是轮产生滚动的条件。如图5.13
阻碍轮与接触面在接触处的相互滑动,但不阻碍滑动,相反还是轮产生滚动的条件。如图5.13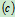 所示,只有足够大的
所示,只有足够大的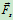 与拉力
与拉力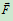 形成足够大的主动力偶才能克服滚动摩阻力偶
形成足够大的主动力偶才能克服滚动摩阻力偶
 ,使滚子滚动。
,使滚子滚动。
下面说明为什么滚动比滑动省力。
使重为 的物块滑动所需拉力
的物块滑动所需拉力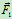 为
为 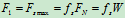
使重为的滚子滚动所需的拉力 为
为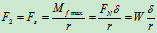
一般情况下: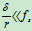 故有
故有
 ,
,
上面两式说明,滚子在较小的主动力作用下产生滚动,其滑动摩擦力远远小于最大静摩擦力。
