第四节 线性方程组的解
线性方程组的一般形式为
（Ⅰ）
还可表示为 Ax=b,
其中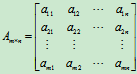
被称为系数矩阵。
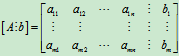称为增广矩阵。
， 
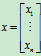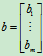
当b =0时，称方程组Ax=0为齐次线性方程组，
当b≠0时，称方程组Ax=b为非齐次线性方程组。
如
的系数矩阵是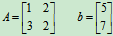
，是非齐次线性方程组。
如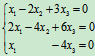
的系数矩阵是
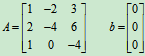，是齐次线性方程组。
第一章介绍了利用行列式的性质来讨论线性方程组的解，下面我们将介绍利用矩阵的性质来讨论线性方程组的解。
定理5 设线性方程组（Ⅰ）的增广矩阵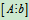
可由初等变换化为
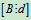，则Ax=b与Bx=d是同解的方程组
注意：如果是齐次线性方程组b =0，只需对其系数矩阵进行初等变换换。
定理5可知求解线性方程组无论是齐次线性方程组还是非齐次线性方程组，首先将其系数矩阵A或增广矩阵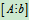
施以初等行变换化简成为行最简形矩阵，再利用系数矩阵的秩数讨论其解。下面分别讨论齐次线性方程组和非齐次线性方程组解的情况。
1. 齐次线性方程组的解
定理6 齐次线性方程组
有非零解的充分必要条件是R(A)<n 。
证明：必要性
已知方程组Ax=0有非零解，用反证法证明。设R（A）=n，则在A 中必有一个n阶非零子式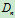
，从而
所对应的n个方程只有零解，这与已知矛盾。
因此R（A）≠n，即R（A）<n。
充分性
已知R（A）=r<n，则A的行最简形矩阵只含r个非零行，其余n-r行都为零，这n-r个行所对应的变量是自由变量，可以任意取值，所以，可知方程组有非零解。
例7 求解线性方程组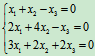
解：系数矩阵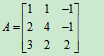
将A施以初等行变换
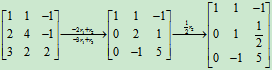
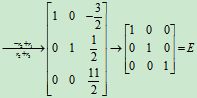
可知R（E）=3，方程组Ex=0只有零解。
又知方程组Ax=0与Ex=0是同解的，所以Ax=0只有零解。
例8 求解齐次线性方程组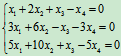
解：系数矩阵
将A施以初等行变换
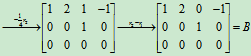
B为最简形矩阵，R（B）=2〈3，由定理6知，方程组Bx=0有非零解
B所对应的方程组为
这个方程组中有4个未知量，两个方程，故应有4-2=2个自由未知量。
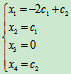
用向量表示为
此解是方程组Bx=0的通解，再由定理5知，它也是方程组Ax=0的通解。
2. 非齐次线性方程组解
对于非齐次线性方程组
如果系数矩阵A是可逆矩阵（或满秩矩阵），其解为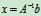
如果系数矩阵A是非满秩矩阵，其解的情况较复杂，可能无解，可能有唯一解，也可能有无穷多解。
定理7 对于非齐次线性方程组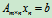
有解的充分必要条件是R(A)= R
当R(A)=R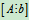
=n时，方程组有唯一解
当R(A)=R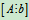 
<n时，方程组有无限多解
当R(A)<R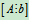
时，方程组无解
证明：必要性
已知方程组Ax=b 有解，用反证法证明。设R(A)<R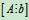
，则将
化为行最简形矩阵，可得其最后一个非零行所对应的方程为0=1，这与方程组有解相矛盾，因此R(A)=R
充分性
当R(A)=R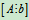
=n时，方程组没有自由未知量，只有唯一解。
当R(A)=R 
<n时，将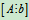
化为行最简形矩阵可知，方程组有n-r个自由未知量，可令它们分别取
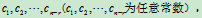则方程组解中含有n-r个任意常数，因而，有无穷多个解。
当R(A)<R
时，可得方程组无解。证毕。
求解非齐次线性方程组，只要将增广矩阵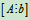
化为行阶梯形矩阵，即可判断其是否有解；若有解，再进一步将化为行最简形矩阵，写出其通解。
例9 求解非齐次线性方程组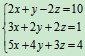
解：其增广矩阵为
，对其进行初等行变换
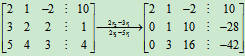
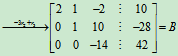
B是行阶梯形矩阵，R（B）=3，即R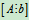
=3。
由于R（A）=R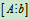
=3=n，可得方程组有唯一解。
再将B化为行最简形矩阵，
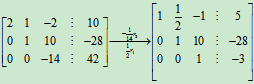
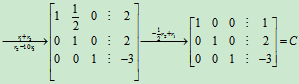
C为行最简形矩阵，其对应的方程组的解为
方程组Ax=b 与之同解，所以Ax=b 有唯一解x=1，y=2，z=-3。
例10 求解非齐次线性方程组
解：其增广矩阵为
，对其进行初等行变换
可见R（A）=R（B）=2〈3，由定理7可得方程组有无穷多解。
再将B化为行最简形矩阵
C为行最简形矩阵，其对应的方程组为
这个方程组中有3个未知量，两个方程，则必有1个自由未知量。
设z=c（c为任意常数）
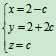
所以原方程组有无穷多个解，其通解为x=2-c，y=2+2c，z=c。
用向量表示为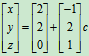
例11 求解方程组
解：其增广矩阵为
，
对其进行初等行变换
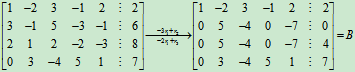
观察B的第2，3行，即可看出R（A）=3，R（B）= R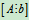
=4
R（A）〈R
所以原方程组无解。
例12 确定λ的值，使下列线性方程组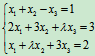
（1）有唯一解；（2）有无穷多解；（3）无解。
解：其增广矩阵为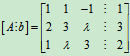
，对其进行初等行变换
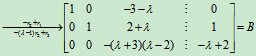
由此可得，如果λ≠2和λ≠-3，R（A）=R
=3，方程组有唯一解；
如果λ=2，则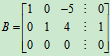
，R（A）=R
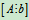=2〈3，方程组有无穷多解；
如果λ=-3，则
，R（A）=2〈R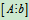
=3，方程组有无解。
