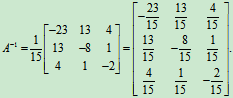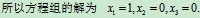矩阵论基础 2.3 方阵的几种运算

第三节 方阵的几种运算

一、方阵的幂

k个n阶方阵连乘，称为方阵A的k次幂，记为A^k.

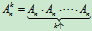
规定

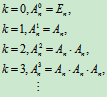
由于矩阵乘法适合结合律，所以方阵的运算满足下列运算规律：

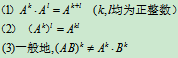
例9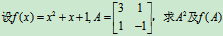

解：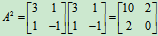

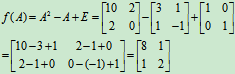
二、方阵的行列式

定义6 由n阶方阵A的元素所构成的行列式称为方阵A的行列式, 记作|A|或detA.

例10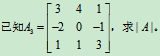

解：

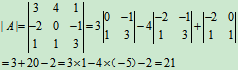
注意：n阶方阵是个数表，n阶行列式是个数值。

方阵的行列式满足以下规律：

(1)|A^T|=|A|;

(2)|lA|=lⁿ|A|;

(3)|AB|=|A||B|，同样地， |BA|=|B||A|

由（3）可知，对于n阶行列式A，B，一般来说AB≠BA，但|BA|=|AB|。

例11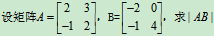

解：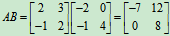

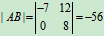
还可以解为

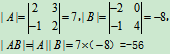
定义7 由n阶方阵A的行列式|A|的各个元素的代数余子式A_ij所构成的n阶方阵的转置矩阵，称为矩阵A的伴随矩阵, 简称伴随阵.记为。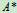

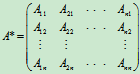
注意：|A|中第i行各元素的代数余子式位于中的第i列，（i=1,2,…，n）。

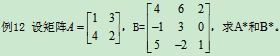
解：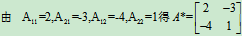

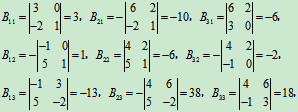
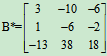
由行列式中的定理可知

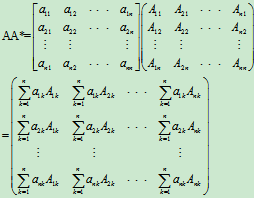
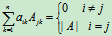
所以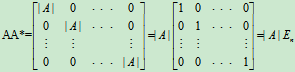

同理可证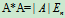

于是有如下结论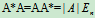

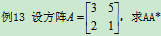
解：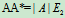

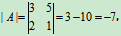
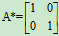
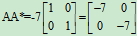
三、方阵的逆

定义8 对于n阶矩阵A, 如果存在n阶矩阵B, 使得AB=BA=E_n,

则矩阵A是可逆矩阵或非奇异矩阵, 并称B为A的逆矩阵, 简称逆阵.

A的逆阵B记为B=A^-1.

可逆矩阵是相互的，B是A的逆矩阵，同样地A也是B的逆矩阵，A与B是互为逆矩阵的

即若AB=BA=E , 则B=A^-1，A=B^-1。

例如，对于二阶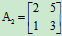方阵与二阶方阵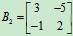，因为

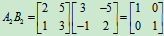
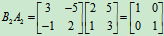
A与B是可逆矩阵，且互为逆矩阵。

逆矩阵具有如下性质：

（1）唯一性: 如果矩阵A是可逆的, 那么A的逆阵是唯一的.

证明：因为如果B_n和C_n都是A的逆矩阵, 则有

AB=BA=E, AC=CA=E,

于是 B=BE=B(AC)=(AB)C=EC=C

即 B=C

所以逆矩阵是唯一的.

(2)若A可逆, 则A^-1也可逆, 且(A^-1)^-1=A;

(3)若A可逆, 数k¹0, 则kA 可逆, 且;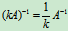

证明：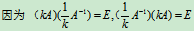

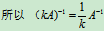
(4)若A可逆, 则A^T也可逆, 且(A^T )^-1=(A^-1)^T .

证明：因为

A^T(A^-1)^T=(A^-1A)^T=E^T=E.

(A^-1)^T A^T =( A A^-1)^T=E^T=E.

所以 (A^T )^-1=(A^-1)^T .

(5)若A、B为同阶可逆矩阵, 则AB亦可逆, 且(AB )^-1=B ^-1A^-1.

这是因为

(AB)(B^-1A^-1)=A(BB^-1)A^-1=AEA^-1=AA^-1=E.

(B^-1A^-1) (AB) = B^-1 (A^-1 A) B = B^-1EB=B^-1B=E.

所以 (AB )^-1=B ^-1A^-1.

该性质也可以推广到有限个矩阵，设A，B，…，C都是可逆的方阵，则有

（AB…C）^-1=C^-1…B^-1A^-1。

定理1 n阶方阵A可逆的充分必要条件是|A|≠0，且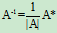

证 必要性：

由已知A可逆，知存在一个n 阶方阵A^-1，使得

AA^-1=A^-1A=E_n，

又因为 |AA^-1|=|A^-1||A|=|E_n|=1，

所以 |A|¹0,

由伴随矩阵的性质 AA* =A*A=|A|E,

得 ,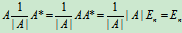

同理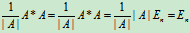

所以, 按逆阵的定义, 即知A可逆, 且有

.

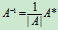充分性（略）

综合起来, 矩阵A可逆Û|A|¹0; 若A可逆, 则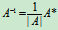

定理1不仅给出了逆矩阵存在的冲要条件，而且给出了求逆矩阵的一种方法，即先求出已知方阵的行列式|A|，如果|A|¹0，可知A可逆，进一步计算出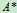，那么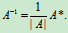

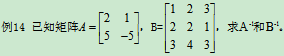
解：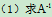

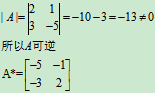
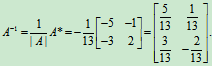
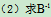
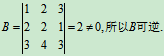
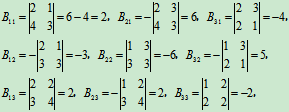
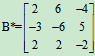
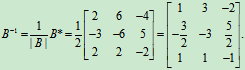
利用矩阵可逆的性质，可以解决许多复杂的问题。

例如：设线性方程组Ax=b，如果A是n阶可逆方阵，那么将方程两边同时左乘A^-1，得

A^-1 Ax= A^-1 b

则x= A^-1 b 就是线性方程组Ax=b的解。

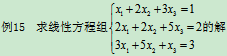
解：已知系数矩阵

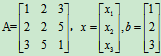
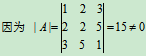
所以A是三阶可逆方阵。