一、矩阵的加法
设A,B是m行,n列的同型矩阵
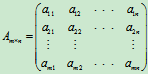 ,
,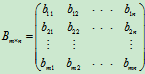
把它们对应位置上的元素相加得到的矩阵,称为A与B的和,记作A+B
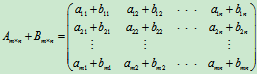
例1 已知矩阵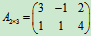 ,
,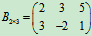 ,求A+B。
,求A+B。
解: A+B=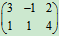 +
+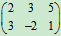 =
=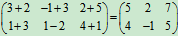
注意:只有同型矩阵才能进行加法运算。
二、数与矩阵相乘
用数l乘以矩阵A的每一个元素而得到的矩阵,称为l与A的乘积, 记为lA或Al, 规定为lA=(laij). 即
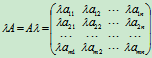
特别地,l=-1时,
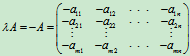 ,
,
该矩阵称为矩阵A的负矩阵。
两个同型矩阵的减法运算可看成A-B=A+(-B)
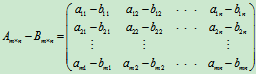
矩阵的加减运算与数和矩阵相乘的运算统称为矩阵的线性运算。
线性运算满足下列运算规律:
(1)加法交换律: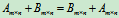
(2)加法结合律: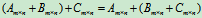
(3)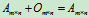
(4)
(5)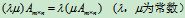
(6)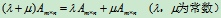
(7)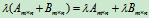
例2 已知矩阵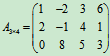 ,
, ,求
,求
(1)A+B;(2)3A;(3)3A-2B
解(1)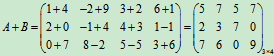
(2)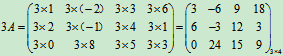
(3)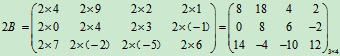
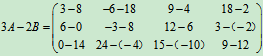
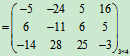
三、矩阵的乘法运算
设有两个线性变换:
设x1,x2,与y1,y2,y3有如下线性关系:
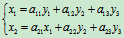 ——(1)
——(1)
其系数矩阵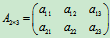
又设y1,y2,y3与z1,z2有如下线性关系:
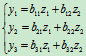 . ——(2)
. ——(2)
其系数矩阵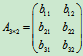
若想求出从x1、x2与z1、z2的线性变换, 可将(2)代入(1), 便得
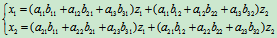 . ——(3)
. ——(3)
其系数矩阵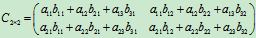
线性变换(3)可看成是先作线性变换(2)再作线性变换(1)的结果. 我们把线性变换(3)叫做线性变换(1)与(2)的乘积, 相应地把所对应的矩阵定义为(1)与(2)所对应的矩阵的乘积, 即
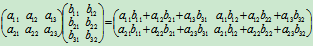 .
.
定义4 设Am×p=(aij) m×p是一个m´p矩阵, B p×n =(Bij) p×n是一个p´n矩阵, 那么矩阵A与矩阵B的乘积记为AB, 规定为m´n矩阵Cm´n=(cij) m´n, 其中
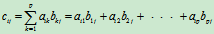 (i=1, 2,
×
×
×, m; j=1, 2,
×
×
× n).
(i=1, 2,
×
×
×, m; j=1, 2,
×
×
× n).
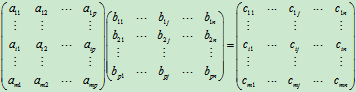
例3 设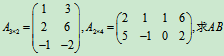
解: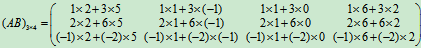
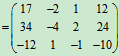
必须注意: 只有当左矩阵的列数等于右矩阵的行数时, 两个矩阵才能相乘.
矩阵乘法的几种特殊情况:
(1)如果A是n元行矩阵,B是n元列矩阵,那么AB是一个数值,BA是一个n阶方阵。
 ,
,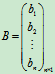
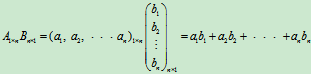 ,
,
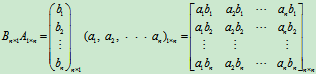
(2)如果A是m×n阶矩阵,
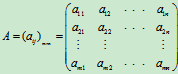 ,B是n元列向量
,B是n元列向量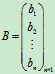 ,那么
,那么
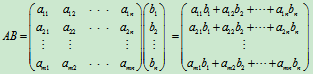
(3)单位矩阵乘以任意矩阵还等于原矩阵。
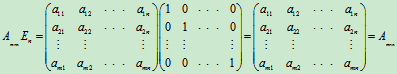
同理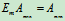
单位矩阵相当于数中的"1"。
矩阵的乘法满足下列运算规律:
(1)结合律 (AB)C=A(BC);
(2) l(AB)=( lA)B=A(lB). (其中l为数);
(3) 分配律 A(B+C)=AB+AC, (B+C)A=BA+CA。
例4 设矩阵A=[1,3,5],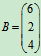 ,
,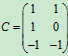 ,求AB,BA,AC
,求AB,BA,AC
解: 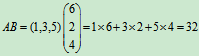
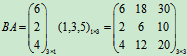
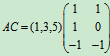
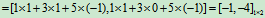
例5 设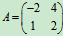 ,
,
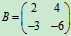 , 求AB及BA.
, 求AB及BA.
解 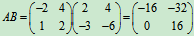 ,
,
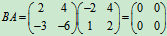
由上面的例子可以得出如下结论:
1.矩阵的乘法一般不满足交换律,即AB≠BA,可从下面几个方面说明
(1)当AB可以相乘时,BA未必可以相乘,如A2×3与B3×4,AB有意义,但BA无意义。
(2)即使A=Am×n ,B=Bn×m,AB和BA都有意义,但AB是m阶方阵,BA是n阶方阵,所以AB≠BA。
(3)即使A,B都是n阶方阵,AB也不一定等于BA,见例5。
2.两个非零矩阵相乘可以是零矩阵,即A≠O,B≠O,但AB=O;反之,即使AB=O,也不能得出A=O或B=O的结论。
四、矩阵的转置运算
定义3 把m×n阶矩阵A的行换成同序数的列得到一个n×m阶新矩阵, 叫做A的转置矩阵, 记作AT 或A′
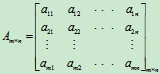 ,
,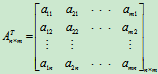
例6 设矩阵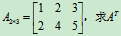
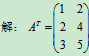
矩阵的转置运算有如下运算规律:
(1)(O)T =O, 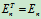 ;
;
(2)(A+B)T=AT+BT;
(3)(AT)T=A;
(4)(kA)T=kAT; (k为常数)
(5)(AB)T=BTAT.
下面证明(5)
设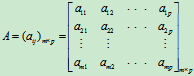
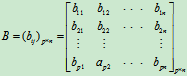
再设
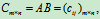
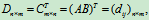
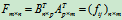
由矩阵的乘法规则,fij等于BT的第i行乘以AT的第j列,BT的第i行即B的第i列
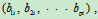 AT的第j列即A的第j 行
AT的第j列即A的第j 行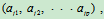 所以
所以
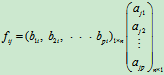
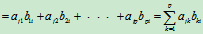
又因为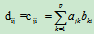
所以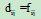
即 (AB)T=BTAT.
例7 设矩阵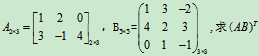
解: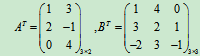
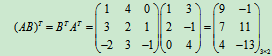
定义4 设A为n阶方阵, 如果满足AT=A, 即aij=aji(i, j=1, 2, × × ×, n)则称A为对称矩阵, 简称对称阵.
例如,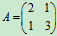 是二阶对称矩阵。
是二阶对称矩阵。
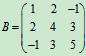 是三阶对称矩阵。
是三阶对称矩阵。
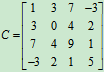 是四阶对称矩阵。
是四阶对称矩阵。
对称阵的特点是: 除主对角线上元素外,其它的元素都以主对角线为对称轴对应相等。
例8 设A,B 都是n阶对称矩阵,证明AB是对称阵的充分必要条件是AB=BA。
证明:由A,B 都是对称矩阵,得AT=A,BT=B,
先证必要性:
设AB都是对称阵,则(AB)T=BTAT=BA=AB
再证充分性:
设AB=BA,于是(AB)T=BTAT=BA=AB,所以AB是对称阵。
