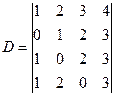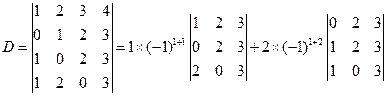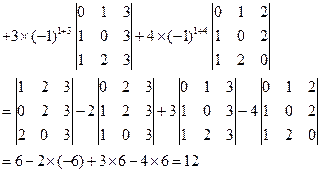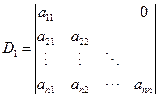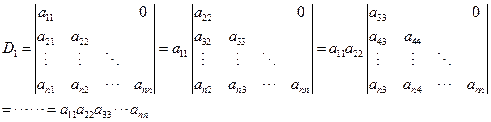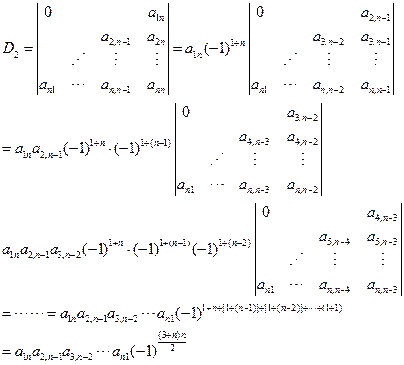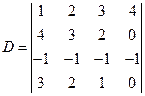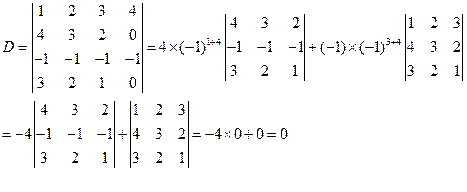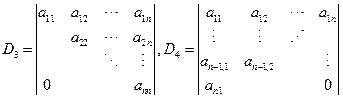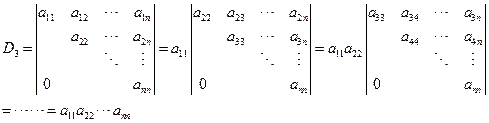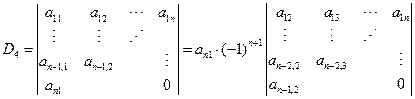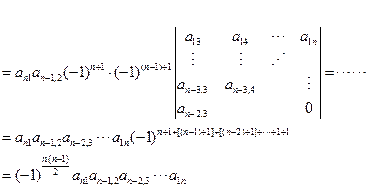第三节 n阶行列式
画n条水平的直线,再画n条铅直的直线,有n2个交叉点,每个交叉点上填上一个数,这样构成n2个数组成的数表。
定义2 由n行,n列共n2个数组成的数表,用下列符号来记
特别规定:当n=1时,一阶行列式D=|a11|= a11
其中Aij为元素aij的代数余子式.
注意:n阶行列式最终是一个数值。
解:按第一行展开
例6 计算下三角行列式(对角线以上的元素全为0)
解:连续按第一行展开
注意:这种下三角行列式的值为主对角线上所有元素之积。此结论以后作公式用
注意:这种下三角行列式的值为副对角线上所有元素之积,再乘以![]() ,此结论以后也作公式用
,此结论以后也作公式用
在n阶行列式中,所有的行与列地位相同,因此,与三阶行列式一样,n阶行列式也可以按任一行或任一列展开。结果如下:
定理2 n阶行列式等于它的任一行(或任一列)的每个元素与其对应的代数余子式的乘积之和,即
或
解:第四列零元素较多,可按第四列展开
例8 计算上三角行列式(对角线以下的元素全为0)
解:连续按第一列展开
先后按第n行,第n-1行,第n-2行,…第二行,第一行展开
由上面的结论知:D1与D3的值为主对角线上所有元素之积;
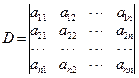
![clip_image002[1] clip_image002[1]](https://images.cnblogs.com/cnblogs_com/begtostudy/WindowsLiveWriter/1.3n_B0B4/clip_image002%5B1%5D_thumb.gif)