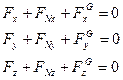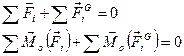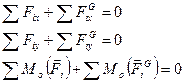教学目标:
1、 对惯性力的概念有清晰的理解。
2、 掌握质点系惯性力简化的方法,能正确地计算平动、定轴转动和平面运动刚体的惯性力主矢和主矩。
3、 能熟练地应用达朗伯原理求解动力学问题。
4、 会计算刚体对任意轴的转动惯量、惯性积(离心转动惯量)和求定轴转动刚体对轴承的附加动压力。
5、 了解惯性主轴、中心惯性主轴、静平衡与动平衡等概念。
本章重点:
1、 惯性力的概念,平动、定轴转动和平面运动刚体惯性力系的简化。
2、 达朗伯原理。
3、 用达朗伯原理求解动力学问题。
本章难点:
1、 惯性力系的简化。
2、 惯性积和惯性主轴的概念。
本章介绍的是求解动力学问题的一种方法。达朗伯原理是通过引入惯性力的概念,把动力学问题用列平衡方程的方法求解。这种方法又称为“动静法”。
一、惯性力
设质点的质量为![]() ,在
,在![]() 力的作用下产生加速度
力的作用下产生加速度![]() ,则定义
,则定义![]() 为质点的惯性力。它是当质点的运动状态发生改变时,由于惯性反抗,对施力物体的一种反抗作用。
为质点的惯性力。它是当质点的运动状态发生改变时,由于惯性反抗,对施力物体的一种反抗作用。
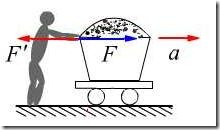
例如:质量为![]() 的小车,在人的推动下沿光滑的直线轨道运动,如图14.1所示。
的小车,在人的推动下沿光滑的直线轨道运动,如图14.1所示。
图14.1
此种情况,小车对人的作用力恰好就是小车本身的惯性力。
二、达朗伯原理
1、质点的达朗伯原理
设质量为![]() 的非自由质点
的非自由质点![]() ,在主动力
,在主动力![]() 和约束力
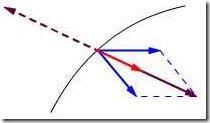
和约束力![]() 的作用下,作曲线运动(图14.2),
的作用下,作曲线运动(图14.2),
图14.2
将上式移项,有:
上式表明:在质点运动的任一瞬时,若把质点的惯性力假想地加在质点上,则作用在质点上的主动力、约束力以及质点的惯性力在形式上组成平衡力系。这称为质点的达朗伯原理。
式(14.1)的投影方程为
2、质点系的达朗伯原理
设由![]() 个质点组成的质点系,其中第
个质点组成的质点系,其中第![]() 个质点的质量为
个质点的质量为![]() ,加速度为
,加速度为![]() ,所受的力为:
,所受的力为:
质点的惯性力为:
由质点的达朗伯原理,有:
表示成力系形式为:
上式表明:在质点系运动的任一瞬时,若假想地把各个质点的惯性力加在各个质点上,则作用在质点系上的外力系和质点系的惯性力系在形式上组成一平衡力系。这称为质点系的达朗伯原理。
一般情况下,式(14.2)有六个投影方程:
对于平面力系,有: