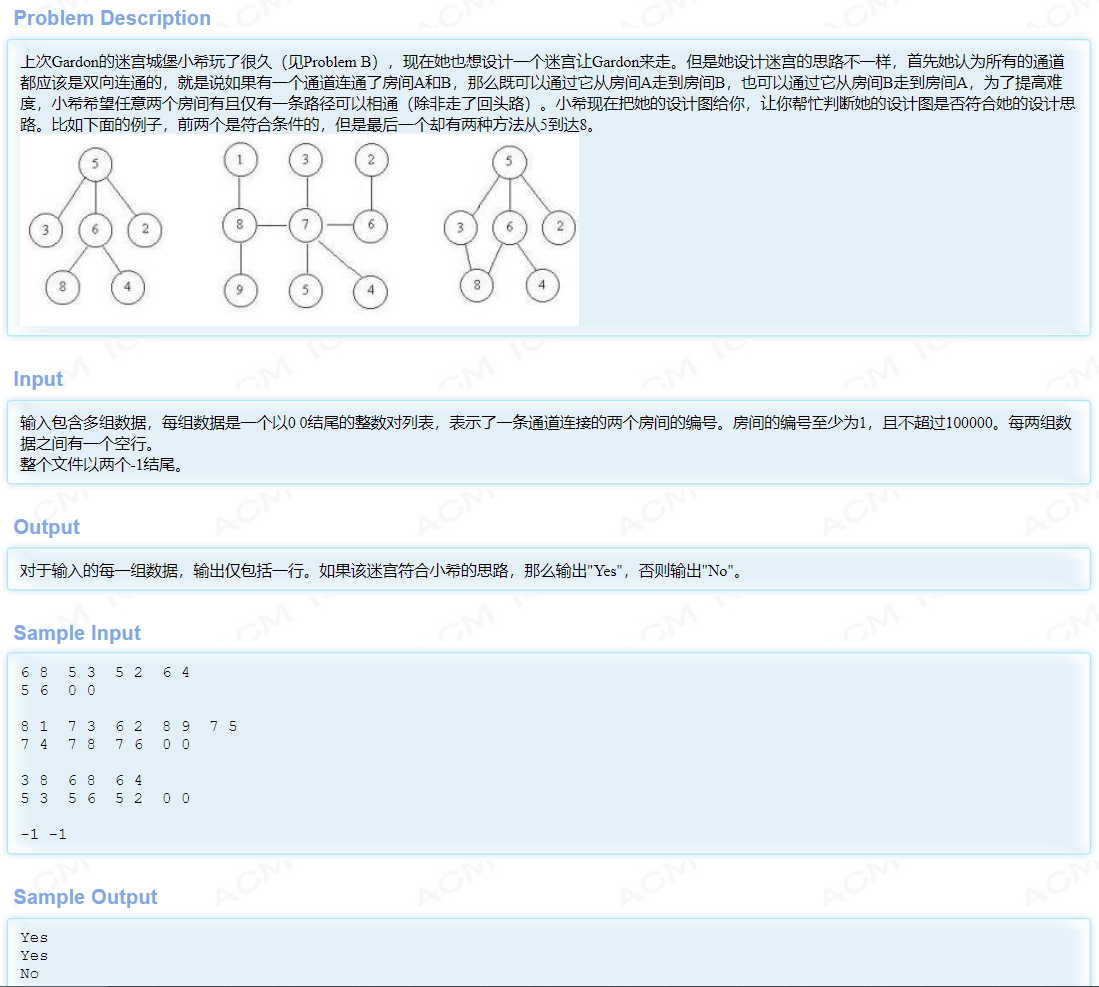
并查集判环
思路: 并查集判环,挺简单的,如果刚开始就指向了一个根,后面又指向了他,说明就成环了(这里不考虑数据重复,比如2->3,2->3)。这个题还有一个点要注意,单次数据可能不止一张图!
package 记录.HDU;
import java.util.HashSet;
import java.util.Scanner;
public class H1272 {
public static int []F;
public static int []vis;
public static int findFather(int x) {
int a = x;
while (x != F[x]) x = F[x];
while (a != F[a]) {
int z = a;
a = F[a];
F[z] = x;
}
return x;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int a, b;
int sum = 0;
F = new int[100010];
vis = new int[100010];
for (int i = 1; i < 100010; i++) {
F[i] = i;
}
boolean flag = false;
while (true) {
a = sc.nextInt();
b = sc.nextInt();
if (a == b && a == 0) {
sum = 0;
for (int i = 1; i < 100010; i++) {
if (vis[i] == 1 && F[i] == i) {
sum++;
if (sum > 1) {
flag = true;
break;
}
}
}
System.out.println(flag == true ? "No" : "Yes");
// 初始化
F = new int[100010];
vis = new int[100010];
for (int i = 1; i < 100010; i++) {
F[i] = i;
}
flag = false;
continue;
}
if (a == b && a == -1) {
break;
}
int fa = findFather(a);
int fb = findFather(b);
vis[a] = 1;
vis[b] = 1;
if (flag == false) {
// 如果a和b的节点的根不一致,那么让他们相连
if (fa != fb) {
F[fa] = fb;
// 如果他们的节点一致的话,说明之前已经连接过,那么此时成环?
} else {
flag = true;
}
}
}
}
}
dfs判环,代码来自
思路: 首先保证图的连通性,然后再判断边 + 1 == 点(这样能判断成环,思考为什么?)。
#include<bits/stdc++.h>
using namespace std;
int T, n, m;
const int maxn = 100000 + 10;
vector<int>G[maxn];
bool vis[maxn];
void init() {
for(int i = 0; i < maxn; i++) G[i].clear(), vis[i] = 0;
}
void dfs(int u) {
if(vis[u])return;
//cout<<u<<endl;
vis[u] = 1;
for(int i = 0; i < G[u].size(); i++) {
dfs(G[u][i]);
}
}
int main() {
int x, y, c;
while(cin >> x >> y && (x + y >= 0)) {
m = 1;
n = 0;
set<int>s;
s.insert(x);
s.insert(y);
if(x == 0 && y == 0) {
cout<<"Yes"<<endl;
continue;
}
init();
G[x].push_back(y);
G[y].push_back(x);
while(cin >> x >> y && (x + y)) {
s.insert(x);
s.insert(y);
G[x].push_back(y);
G[y].push_back(x);
m++;
c = x;
}
dfs(c);
for(set<int>::iterator it = s.begin(); it != s.end(); ++it) {
if(vis[*it])n++;
}
if(n == m + 1)cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
return 0;
}