JZ12 矩阵中的路径
描述
请设计一个函数,用来判断在一个n乘m的矩阵中是否存在一条包含某长度为len的字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入该格子。例如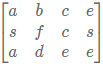 矩阵中包含一条字符串"bcced"的路径,但是矩阵中不包含"abcb"路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入该格子。
矩阵中包含一条字符串"bcced"的路径,但是矩阵中不包含"abcb"路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入该格子。
示例1
输入:[[a,b,c,e],[s,f,c,s],[a,d,e,e]],"abcced"返回值:true
分析
先说一下这道题使用的方法是深度优先算法dfs和回溯
dfs
深度优先算法就是一种图的遍历算法,简单来说就是从某个顶点的分支开始,尽可能深沿图的深度访问没有访问过的节点直至此分支全都访问完毕
解题
本人代码使用非递归实现了dfs+回溯,其中,一开始需要寻找矩阵中所有符合初始节点的字符位置,通过两个while循环完成算法
代码
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param matrix char字符型二维数组
* @param word string字符串
* @return bool布尔型
*/
public boolean hasPath (char[][] matrix, String word) {
/**
* 访问节点对象
*/
class HasPathNode{
char letter;
int x;
int y;
//标志其节点周围是否访问过
boolean visitUp = false;
boolean visitDown = false;
boolean visitLeft = false;
boolean visitRight = false;
HasPathNode(char letter,int x,int y) {
this.letter = letter;
this.x = x;
this.y = y;
//给出边界节点的判定
if (x == 0){
this.visitUp = true;
}
//给出边界节点的判定
if (y == 0) {
this.visitLeft = true;
}
//给出边界节点的判定
if (x == matrix.length -1) {
this.visitDown = true;
}
//给出边界节点的判定
if (y == matrix[0].length -1) {
this.visitRight = true;
}
}
}
// write code here
char words[] = word.toCharArray();
//把需要判断的字符放入链表
LinkedList<Character> wordsQueue = new LinkedList<>();
for (char item : words) {
wordsQueue.offer(item);
}
//已经经过判断的字符
Stack<Character> usedWords = new Stack<>();
//符合条件的初始节点
Queue<HasPathNode> firstLetterQueue = new LinkedList<>();
//寻找符合条件的初始节点
for (int i = 0;i<matrix.length;i++) {
for (int j = 0;j<matrix[0].length;j++) {
if (matrix[i][j] == wordsQueue.peek()) {
HasPathNode node = new HasPathNode(matrix[i][j],i,j);
firstLetterQueue.offer(node);
}
}
}
//如果没有符合的则返回false
if (firstLetterQueue.size() == 0)
return false;
//初始节点放入已使用
usedWords.push(wordsQueue.poll());
while (firstLetterQueue.size() >0) {
Stack<HasPathNode> nodeStack = new Stack<>();
nodeStack.push(firstLetterQueue.poll());
while (nodeStack.size() >0) {
if (nodeStack.peek().visitUp == false && matrix[nodeStack.peek().x - 1][nodeStack.peek().y] == wordsQueue.peek()) {
//上
HasPathNode node = new HasPathNode(wordsQueue.peek(),nodeStack.peek().x - 1,nodeStack.peek().y);
nodeStack.peek().visitUp = true;
nodeStack.push(node);
nodeStack.peek().visitDown = true;
usedWords.push(wordsQueue.poll());
}else if (nodeStack.peek().visitDown == false && matrix[nodeStack.peek().x + 1][nodeStack.peek().y] == wordsQueue.peek()) {
//下
HasPathNode node = new HasPathNode(wordsQueue.peek(),nodeStack.peek().x + 1,nodeStack.peek().y);
nodeStack.peek().visitDown = true;
nodeStack.push(node);
nodeStack.peek().visitUp = true;
usedWords.push(wordsQueue.poll());
}else if (nodeStack.peek().visitLeft == false && matrix[nodeStack.peek().x][nodeStack.peek().y - 1] == wordsQueue.peek()) {
//左
HasPathNode node = new HasPathNode(wordsQueue.peek(),nodeStack.peek().x,nodeStack.peek().y - 1);
nodeStack.peek().visitLeft = true;
nodeStack.push(node);
nodeStack.peek().visitRight = true;
usedWords.push(wordsQueue.poll());
}else if (nodeStack.peek().visitRight == false && matrix[nodeStack.peek().x][nodeStack.peek().y + 1] == wordsQueue.peek()) {
//右
HasPathNode node = new HasPathNode(wordsQueue.peek(),nodeStack.peek().x,nodeStack.peek().y + 1);
nodeStack.peek().visitRight = true;
nodeStack.push(node);
nodeStack.peek().visitLeft = true;
usedWords.push(wordsQueue.poll());
}else {
nodeStack.pop();
if (usedWords.size() != 1) {
wordsQueue.addFirst(usedWords.pop());
}
}
if (wordsQueue.size() == 0)
return true;
}
}
return false;
}