剑指offer：JZ8 二叉树的下一个结点

JZ8 二叉树的下一个结点

描述

给定一个二叉树其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点，同时包含指向父结点的next指针。下图为一棵有9个节点的二叉树。树中从父节点指向子节点的指针用实线表示，从子节点指向父节点的用虚线表示

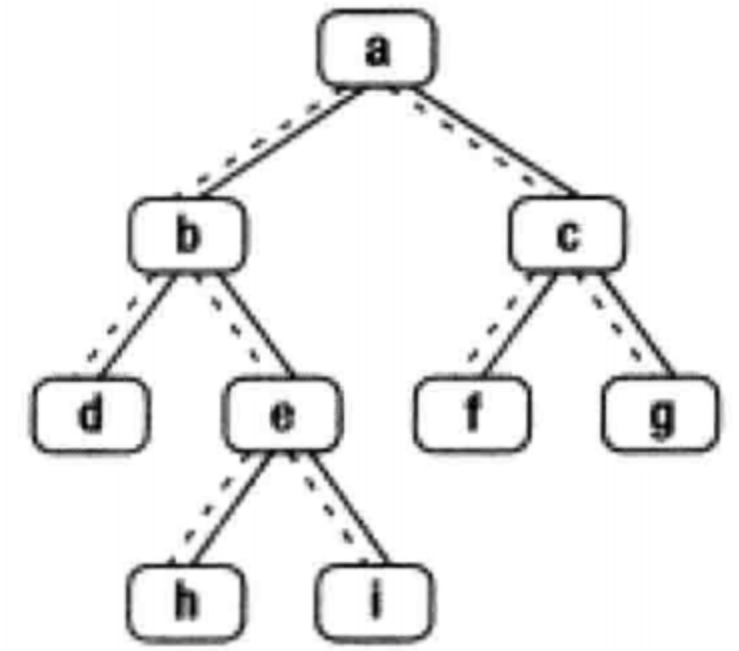
示例:
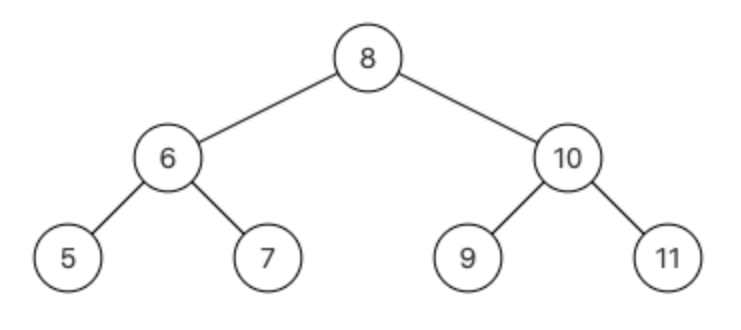
输入:{8,6,10,5,7,9,11},8
返回:9
解析:这个组装传入的子树根节点，其实就是整颗树，中序遍历{5,6,7,8,9,10,11}，根节点8的下一个节点就是9，应该返回{9,10,11}，后台只打印子树的下一个节点，所以只会打印9，如下图，其实都有指向左右孩子的指针，还有指向父节点的指针，下图没有画出来

分析

初拿到这道题，很明显看出是一个二叉树的中序遍历就可以解决的问题，但是仔细看了题目之后，发现，题目会给两个参数，而这两个参数组装成的是一个二叉树节点（可以是其中树的任意节点），这样的话，如果使用普通的遍历方法直接做，就会有问题，需要多一步遍历这个节点的next找到整棵树的根节点，之后使用dfs进行中序遍历得到结果。

代码

      /**
     * JZ8 二叉树的下一个结点
     * @param pNode
     * @return
     */
    public TreeLinkNode GetNext(TreeLinkNode pNode) {
        //提出题目中要求对比的值
        Integer value = pNode.val;
        //通过不断的寻找next找到整棵树的根节点
        while (pNode.next != null) {
            pNode = pNode.next;
        }
        //结果队列
        Queue<TreeLinkNode> queue = new LinkedList<>();
        //dfs遍历使用的栈，储存没有遍历过的节点用
        Stack<PosNode> treeStack = new Stack<>();
        //根节点
        PosNode rootNode = new PosNode(pNode);
        //根节点加入栈
        treeStack.push(rootNode);
        //如果所有节点都已经遍历过就跳出循环
        while (treeStack.size() > 0) {
            //中序遍历，先遍历左子树
            if (treeStack.peek().node.left != null && treeStack.peek().visitLeft == false) {
                PosNode posNode = new PosNode(treeStack.peek().node.left);
                //证明左子树访问过
                treeStack.peek().visitLeft = true;
                treeStack.push(posNode);
            }else {
                //把节点值值存储在结果队列中
                queue.offer(treeStack.peek().node);
                //证明左子树访问过
                treeStack.peek().visitLeft = true;
                //开始遍历右子树
                if (treeStack.peek().node.right != null && treeStack.peek().isVisitRight == false) {
                    PosNode posNode = new PosNode(treeStack.peek().node.right);
                    treeStack.peek().isVisitRight = true;
                    treeStack.push(posNode);
                }else {
                    //如果右子树也遍历过或者为空的话
                    treeStack.peek().isVisitRight = true;
                    //通过出栈寻找左右子树都没有遍历过的节点
                    while (treeStack.size() != 0 && treeStack.peek().isVisitRight == true && treeStack.peek().visitLeft == true)
                        treeStack.pop();
                }
            }
        }

        //存储的中序遍历结果进行值的比较找出结果
        while (queue.size() != 0) {
            if (queue.peek().val != value) {
                queue.poll();
            }else {
                queue.poll();
                return queue.peek();
            }
        }

        //找不到的话返回空值
        return null;
    }

    /**
     * 保存节点以及记录节点的左右子树是否访问过的表质量
     */
    class PosNode{
        TreeLinkNode node;
        boolean visitLeft = false;
        boolean isVisitRight = false;

        PosNode(TreeLinkNode node) {
            this.node = node;
        }
    }

总结

需要熟练使用代码来遍历二叉树，本人的方法使用内存占用较高，后续可以去除结果队列，直接在遍历中使用标志量记录结果返回。