二维数组中的最大联通子数组

题目：

输入一个二维整形数组，数组里有正数也有负数。

求所有子数组的和的最大值。

思路：

实现思路如下：

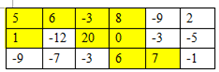
1.先找出二维数组中不包含负数的直接相邻（上下左右相邻）的正整数块。如下图

2.然后转化建模，将该“二维表”与“图”转化，转化方法如下：将每个正整数块看做一个“正元素，将每一个负数看做一个“负元素”，将每一个“正元素”和每一个“负元素”分别作为“图”的结点，其中每个正整数块的和的相反数作为相应“正元素”结点的权值，每个负数的值的相反数作为“负元素”结点的权值，具有直接相邻关系的表中元素，具有双向连通性，结点A与结点B的权值的和定义为从结点A到结点B的“代价”，则该题求最大联通子数组的问题成功转化为求图中的最短路径问题，用弗洛伊德算法可以求出图中每对结点之间的最短路径，遍历求出其中的“代价”最小的一组，再还原出其最短路径，即可找出最大联通子图。

源代码：

#include<iostream>
using namespace std;
int zuida(int n, int a[], int *sm, int *mm);

void main()
{
    int m, n, i, j, sm, mm, t2;
    int sum, max;
    int up[100], down[100], t[100];
    int a[100][100], b[100];
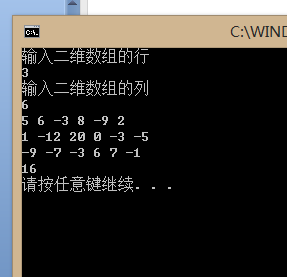
    cout << "输入二维数组的行" << endl;
    cin >> m;
    cout << "输入二维数组的列" << endl;
    cin >> n;
    for (i = 0; i<m; i++)
    {
        for (j = 0; j<n; j++)
        {
            cin >> a[i][j];
        }
    }

    for (i = 0; i<m; i++)
    {
        for (j = 0; j<n; j++)
        {
            b[j] = a[i][j];
        }
        sum = zuida(n, b, &sm, &mm);
        up[i] = sum;
        down[i] = mm;
        t[i] = sum;

    }
    t2 = t[0];
    for (i = 0; i + 1<m; i++)
    {
        if (up[i] <= down[i + 1] && down[i] >= up[i + 1])
        {
            t2 += t[i + 1];
        }
        for (j = up[i]; j<up[i + 1]; j++)
        {
            if (a[i + 1][j]>0) t2 += a[i + 1][j];                   //判别独立正数
        }

    }
    cout << t2 << endl;

}


int zuida(int n, int a[], int *sm, int *mm)
{
    int b[100] = { 0 };
    int i, sum1 = 0, max1 = 0;
    for (i = 0; i<n; i++)
    {
        if (sum1<0)
        {
            sum1 = a[i];
        }
        else
        {
            sum1 = sum1 + a[i];
        }
        b[i] = sum1;
    }
    max1 = b[0];
    for (i = 0; i<n; i++)
    {
        if (max1<b[i])
        {
            max1 = b[i];
            *mm = i;
        }
    }
    for (i = *mm; i >= 0; i--)
    {
        if (b[i] == a[i])
        {
            *sm = i;
            break;
        }
    }
    return max1;
}

4程序截图

总结：

思路应该是可行的，但是工作量比较大，所以当时没有实现。