重拾(manacher),真切感受到了他的妙处
首先,考虑到回文串分奇数和偶数两种情况,需要分类讨论,所以我们可以考虑在所有字符之间插入一个没有用过的符号'#'
然后边界问题不好处理,所以可以在字符串的开头加上一些奇怪的符号'~'
接下来就是(manacher)的正文部分了
我们定义(p_i)表示以i为对称中心,能拓展的回文数量
发现我们可以(O(N^2))的暴力做法:一直向外拓展,直到不匹配
在定义(mr)表示我们经过的,最靠右边的点,在记录一个(mid)表示这个最靠右的点是由哪一个对称轴转移过来的
然后发现,对于每一个(i),我们没有必要都去拓展,我们分几种情况讨论:
(Case1: mid<i<mr)
由于([mid - mr, mid + mr])是回文的,设(j)为(i)以(mid)为中心的对称点,根据对称性那么我们有:([j-p_j, j+p_j]=[i-p_i, i+p_i])
但是当(i+p_i>mr)时,我们无法保证上述情况相等(设(mr)以$ mid(为中心的对称点为)x(,因为)j-p_j<x(,所以无法保证相等,详见下图)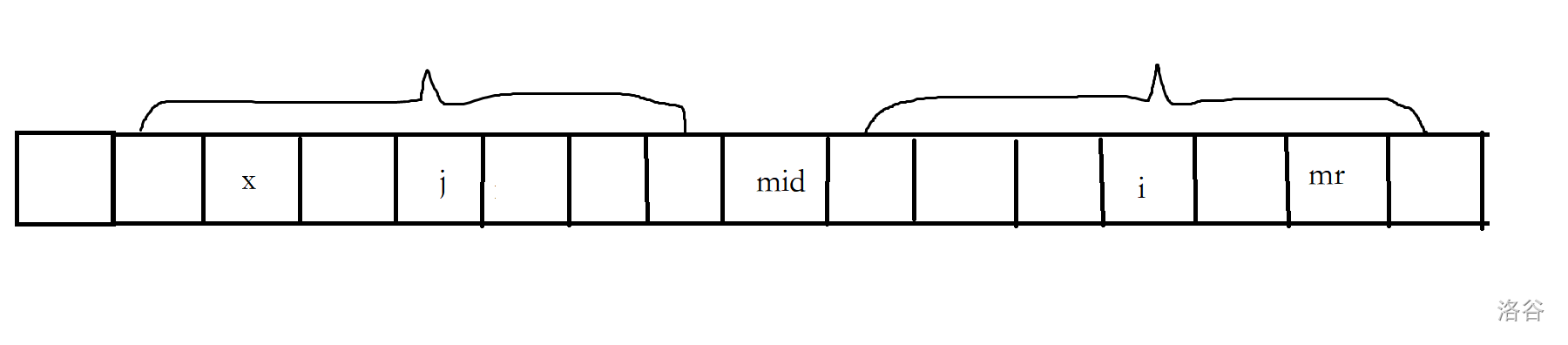 所以对于)Case1(,我们可以直接让)p[i]=min(p[j], mr - i + 1)$,然后暴力拓展即可
(Case2:i<mr)
这个时候我们不能求出i的对称点,直接暴力拓展即可
由于(mr)和$ mid$,不断右移,所以复杂度线性
(Code:)
#include<bits/stdc++.h>
using namespace std;
#define rep(i, s, t) for(int i = s; i <= t; ++ i)
#define maxn 22000005
int n, m, cnt, p[maxn], mid, mr, Ans;
char c[maxn], s[maxn];
void build() {
scanf("%s", c + 1), n = strlen(c + 1), s[++ cnt] = '~', s[++ cnt] = '#';
rep(i, 1, n) s[++ cnt] = c[i], s[++ cnt] = '#';
s[++ cnt] = '!';
}
void solve() {
rep(i, 2, cnt - 1) {
if(i <= mr) p[i] = min(p[mid * 2 - i], mr - i + 1);
else p[i] = 1;
while(s[i - p[i]] == s[i + p[i]]) ++ p[i];
if(i + p[i] > mr) mr = i + p[i] - 1, mid = i;
Ans = max(Ans, p[i]);
}
printf("%d", Ans - 1);
}
int main() { return build(), solve(), 0; }