题面要求小于等于K的路径数目,我么很自然的想到点分治(不会的就戳我)
这道题的统计答案与模板题不一样的地方是由等于K到小于等于K
那么我们可以把每一个子节点到当前根(重心)的距离排序,然后用类似双指针的方法来求小于等于K的边的数量
但是如果只是双指针统计的话,那么以下不合法的情况显然也会被算进答案:
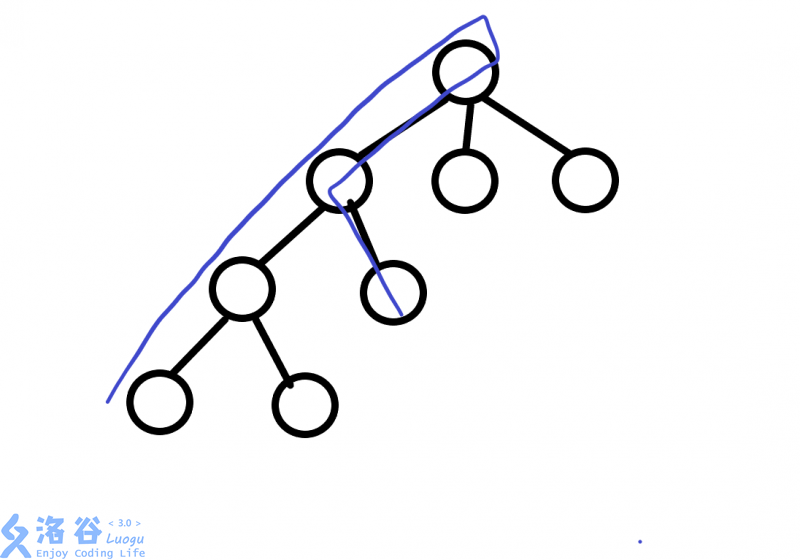
而我们需要的合法路径是长成这样的:
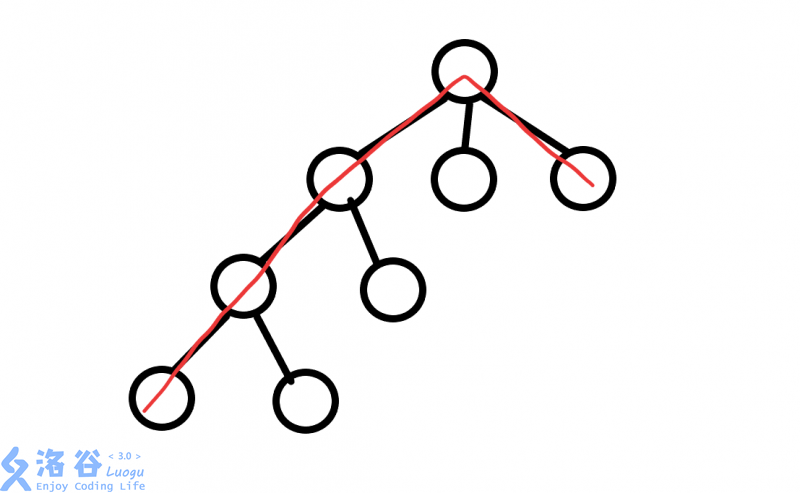
所以我们需要减去上述不合法的路径,怎么减呢?
不难发现,对于所有不合法的路径,都是在当前跟的某一棵子树上的(没有跨越两个子树)
所以我们可以对当前跟节点的每一条边进行遍历,利用容斥的思想减去不合法的路径。
具体操作为:当遍历重心节点的每一个节点时,我们可以重新计算dis,然后把经过了从重心到新遍历的点的边两次的路径剪掉(就是上述不合法路径),最后统计答案即可
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define re register
#define inf 123456789
il int read()
{
re int x = 0, f = 1; re char c = getchar();
while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar();}
while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
return x * f;
}
#define rep(i, s, t) for(re int i = s; i <= t; ++ i)
#define drep(i, s, t) for(re int i = t; i >= s; -- i)
#define Next(i, u) for(re int i = head[u]; i; i = e[i].next)
#define mem(k, p) memset(k, p, sizeof(k))
#define maxn 40005
struct edge{int v, w, next;}e[maxn << 1];
int n, m, head[maxn], cnt, k, ans;
int dp[maxn], vis[maxn], sum, dis[maxn], rt, size[maxn], rev[maxn], tot;
il void add(int u, int v, int w)
{
e[++ cnt] = (edge){v, w, head[u]}, head[u] = cnt;
e[++ cnt] = (edge){u, w, head[v]}, head[v] = cnt;
}
il void getrt(int u, int fr)
{
size[u] = 1, dp[u] = 0;
Next(i, u)
{
int v = e[i].v;
if(v == fr || vis[v]) continue;
getrt(v, u);
size[u] += size[v], dp[u] = max(dp[u], size[v]);
}
dp[u] = max(dp[u], sum - size[u]);
if(dp[u] < dp[rt]) rt = u;
}
il void getdis(int u, int fr)
{
rev[++ tot] = dis[u];
Next(i, u)
{
int v = e[i].v;
if(v == fr || vis[v]) continue;
dis[v] = dis[u] + e[i].w;
getdis(v, u);
}
}
il int doit(int u, int w)
{
tot = 0, dis[u] = w, getdis(u, 0);
sort(rev + 1, rev + tot + 1);
int l = 1, r = tot, ans = 0;
while(l <= r) (rev[l] + rev[r] <= k) ? (ans += r - l, ++ l) : (-- r);
return ans;
}
il void solve(int u)
{
vis[u] = 1, ans += doit(u, 0);
Next(i, u)
{
int v = e[i].v;
if(vis[v]) continue;
ans -= doit(v, e[i].w);
sum = size[v], dp[0] = n, rt = 0;
getrt(v, u), solve(rt);
}
}
int main()
{
n = read();
rep(i, 1, n - 1){int u = read(), v = read(), w = read(); add(u, v, w);}
k = read(), dp[0] = sum = n, getrt(1, 0), solve(rt);
printf("%d", ans);
return 0;
}