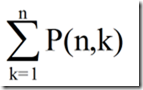Project Euler 76：Counting summations

题目链接

原题：

It is possible to write five as a sum in exactly six different ways:

4 + 1
3 + 2
3 + 1 + 1
2 + 2 + 1
2 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1

How many different ways can one hundred be written as a sum of at least two positive integers?

翻译：

加和计数

将5写成整数的和有6种不同的方式：

4 + 1
3 + 2
3 + 1 + 1
2 + 2 + 1
2 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1

将100写成整数的和有多少种不同的方式？

翻译来源

解题思路：

将100能够拆成整数的和能够有多少种？

1.利用动态规划求解

2.利用数的拆分求解<组合数学中有讲解>

数的拆分法

理论基础，链接中讲到了拆分的理论

P（n，k）的意思就是n拆分成k份的数量

有递推公式：

P（n，k）= P（n-1，k-1） + P（n-k，k）

初始值：

k>n时：P（n，k） = 0

对所有的n，P（n，n）=1，P（n，0）=0

也很显然的发现：

对所有的n，P（n，1）=n，P（n，2） = n/2 的向下取整

证明：P（n，k）= P（n-1，k-1） + P（n-k，k）

忘了。。。

求出所以的P（n，k）矩阵

则n的所以拆分的和是

Java程序：

//  整数n 拆分k份
    void partitions(){
        int limit = 100;
        int count = 0;
        int[][] p = new int[limit+1][limit+1];
        for(int n=0;n<=limit;n++){
            p[n][n] = 1;
            p[n][1] = 1;
            p[n][0] = 0;
        }
        for(int n=1;n<=limit;n++){
            for(int k=1;k<=n;k++){
                p[n][k] = p[n-1][k-1] + p[n-k][k];
                    if(n==limit)
                        count+=p[n][k];
                }
        }
        count = count - 1;
        System.out.println(count);
    }

结果：

//    190569291
//    running time=0s0ms

利用递归程序：

void getPar(){
        int limit = 100;
        int count = 0;
        for(int k=1;k<=limit;k++)
            count+=Par(100,k);
        count = count-1;
        System.out.println(count);
    }

    //递归形式 整数n 拆分k分
    int Par(int n,int k){
        if(k==1||n==k) return 1;
        if(k>n) return 0;
        return Par(n-1,k-1)+Par(n-k,k);
    }

结果：

//    190569291
//    running time=1s869ms

递归时间明显长了许多

动态规划求解

//动态规划求解
    void dp(){
        int limit = 100;
        int[] ways = new int[limit+1];
        ways[0] = 1 ;
        for(int i=1;i<=limit-1;i++){
            for(int j = i;j<=limit;j++)
                ways[j] += ways[j-i];
        }
        System.out.println(ways[limit]);
    }

//    190569291
//    running time=0s0ms

还看不懂

完整java程序：

package Level3;
public class PE076{
    
    void run(){

//        dp();
//        partitions();
//        getPar();
        int res = partitions3(100,100);
        res = res - 1;
        System.out.println(res);
    }
    int  partitions3(int n,int m ){
        if(n<=1) return 1;
        if(m>n) return partitions3(n,n);
        int sum = 0;
        for(int k=1;k<=m;k++)
            sum+=partitions3(n-k,k);
        return sum;
    }
//    190569291
//    running time=10s845ms
    void getPar(){
        int limit = 100;
        int count = 0;
        for(int k=1;k<=limit;k++)
            count+=Par(100,k);
        count = count-1;
        System.out.println(count);
    }
//    190569291
//    running time=1s869ms
    //递归形式 整数n 拆分k分
    int Par(int n,int k){
        if(k==1||n==k) return 1;
        if(k>n) return 0;
        return Par(n-1,k-1)+Par(n-k,k);
    }
    //  整数n 拆分k份
    void partitions(){
        int limit = 100;
        int count = 0;
        int[][] p = new int[limit+1][limit+1];
        for(int n=0;n<=limit;n++){
            p[n][n] = 1;
            p[n][1] = 1;
            p[n][0] = 0;
        }
        for(int n=1;n<=limit;n++){
            for(int k=1;k<=n;k++){
                p[n][k] = p[n-1][k-1] + p[n-k][k];
                    if(n==limit)
                        count+=p[n][k];
                }
        }
        count = count - 1;
        System.out.println(count);
//        for(int n=1;n<=6;n++){
//            for(int k=1;k<=n;k++)
//                System.out.print(p[n][k]+" ");
//            System.out.println();
//        }
        
//        for(int k=0;k<=limit;k++)
//            count+= p[limit][k];
//        count = count - 1;
//        System.out.println(count);
        
    }
//    190569291
//    running time=0s0ms
    //动态规划求解
    void dp(){
        int limit = 100;
        int[] ways = new int[limit+1];
        ways[0] = 1 ;
        for(int i=1;i<=limit-1;i++){
            for(int j = i;j<=limit;j++)
                ways[j] += ways[j-i];
        }
        System.out.println(ways[limit]);
    }
//    190569291
//    running time=0s0ms
    
    
    public static void main(String[] args){
        long t0 = System.currentTimeMillis();
        new PE076().run();
        long t1 = System.currentTimeMillis();
        long t = t1 - t0;
        System.out.println("running time="+t/1000+"s"+t%1000+"ms");
        
    }
}

Python实现

动态规划的效率很高

递归的已经不能忍了

import time 

def PE076():
    res = dp();
#     res = partitions(100,100)
    print res 
def partitions(n,m):
#     limit = 100 
    count = 0 
    if n<=1 : return 1
    if m>n : return partitions(n,n)
    for k in range(1,m+1):
        count = count + partitions(n-k,k)
    return count
#     190569292
# running time=1073.04099989s
def dp():
    limit = 100
    ways = [0]*(limit+1)
    ways[0] = 1 
    for n in range(1,limit):
        for k in range(n,limit+1):
            ways[k] +=ways[k-n]
    return ways[limit]
if __name__=='__main__':
    t0 = time.time()
    PE076()
    print "running time={0}s".format((time.time()-t0))