1. 为什么要初始化权重
为了使网络中的信息更好的传递,每一层的特征的方差(标准差)应该尽可能相等,否则可能会导致梯度爆炸或者消失。
权重初始化的目的是在深度神经网络中前向传递时,阻止网络层的激活函数输出爆炸(无穷大)或者消失(0)。如果网络层的输出爆炸或者消失,损失函数的梯度
也会变得很大或者很小,无法有效后向传递,使得神经网络需要更长的时间才能收敛甚至无法收敛。
矩阵乘法是神经网络中的基本数学操作。在深度神经网络中,前向传递需要在每一层的输入与权重之间执行矩阵相乘,前一层的相乘结果作为后面一层的输入。
举个简单的例子,假设我们有一个网络的输入向量x。训练神经网络的标准做法,是对输入x归一化,让它的值落入一个均值为0,标准差为1的正态分布中。
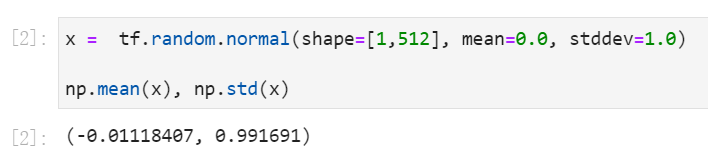
x正态分布
假设我们有一个不含激活函数的100层网络,并且每层都有一个权重矩阵w。为了完成前向传递,我们使每层的输入和权重相乘,总共100次。
事实证明,把网络层的权重值用标准正态分布进行初始化并不好。为了弄明白其原因,我们可以模拟网络的前向传播。
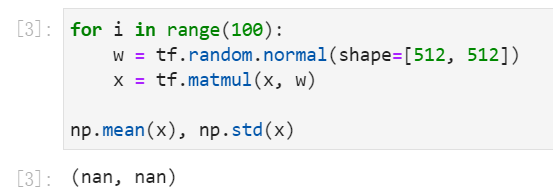
输出爆炸
在100次的矩阵相乘后,输出爆炸(nan)。
看一下前向传递多久会输出爆炸。第28次的输出就为nan了,显然权重初始化的值偏大。
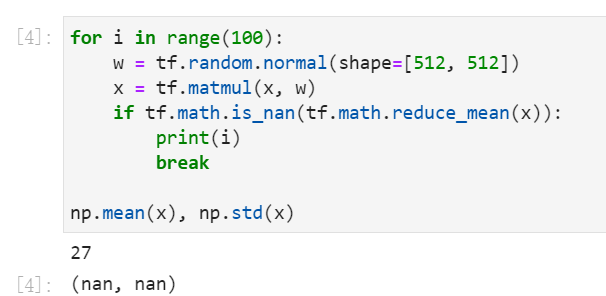
第28次输出爆炸, i=0,...,27
不过我们还得考虑网络层的输出消失的问题。当权重w的初始化值太小的时候,观察一下效果。使用均值为0,标准差0.01的正态分布去初始化权重。

输出消失
上面的前向传递,激活输出消失了。
总结就是,如果权重初始化的值太大或者太小,网络无法有效学习。
2. 如何找到最优的初始化值
如前所述,一次完整的前向传递只需要连续地使网络层的输入和权重进行矩阵相乘就可以。如果输出y是输入x和权重w的矩阵乘积,那么y中第(i)个元素(y_i)如下,
其中(i)是权重w给定行的索引,(k)既是给定列的索引又是输入向量x的元素索引,(n)是x中元素的个数。这个公式可以在Python中表示为:
y[i] = sum([c*d for c,d in zip(a[i], x)])
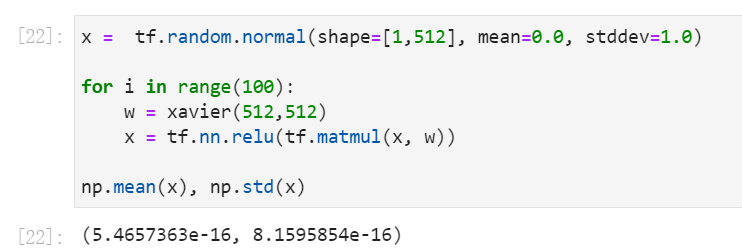
可以证明,在给定的某一层,利用标准正态分布初始化的输入x和权重w的乘积,平均情况下,这个乘积的标准差非常接近网络层的输入单元的数目(如512)的平方根,本例中是(sqrt{512})。

10000次矩阵相乘的平均标准差
如果我们从矩阵乘法的定义来看待这个值就再正常不过了:为了计算y,我们将输入x乘以权重矩阵w的一列512个元素的点积求和,得到y中的一个元素。
在我们下面的例子中使用了标准正态分布来初始化x和w,所以y的每个元素(y_i)都是均值为0,标准差为1。

标准正态分布的2个元素相乘10000次
因此,y的均值为0,方差为512,标准差就为(sqrt{512})。
因此在上面的例子中,经过27次传递后网络层的输出就爆炸了。在我们100层的网络结构中,我们想要的是对于每一层的输出,其标准差为1,这样就可以连续地在网络层之间
进行矩阵相乘,而层的输出不会爆炸或者消失。
如果我们将权重初始值除以(sqrt{512})进行缩小,那么y中各元素值的方差会变成({1} over {512}),即标准差({1} over {sqrt{512}}),如下。
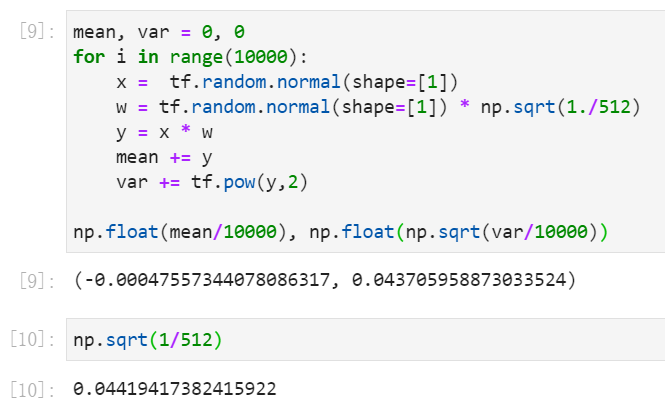
标准差sqrt(1/512)
这意味着y的标准差为1,因为y有512个标准差为({1} over {sqrt{512}})的元素。实验证实如下,

y的标准差1
再运行一下这个100层的网络。首先初始化权重w,用标准正态分布初始化,再除以(1 over sqrt{n}),(n)是网络层的输入数目,本例是(n=512)。
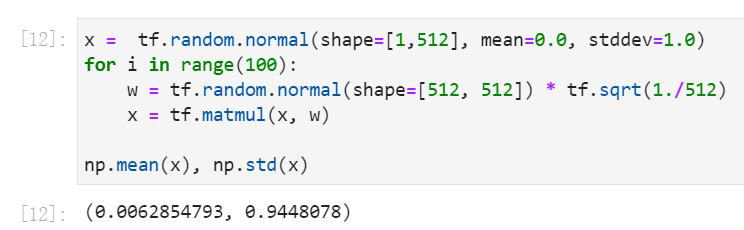
100层网络的输出既不爆炸,也不消失。
可见,100层网络的输出既不会爆炸,也不会消失。
虽然乍一看似乎真的搞定了,但是真正的神经网络模型并不像我们这个例子那么简单。为了简单起见,我们省略了激活函数。但是,在实际中我们永远不会这样做。正是因为有了这些非线性激活函数,深度神经网络才能非常近似地模拟真实世界那些错综复杂的现象,并且生成那些令人惊讶的预测,例如手写样本的分类。
3. Xavier初始化
直到几年前,最常用的激活函数是关于某个给定的值对称的,双曲正切函数和softsign函数就是这类激活函数。
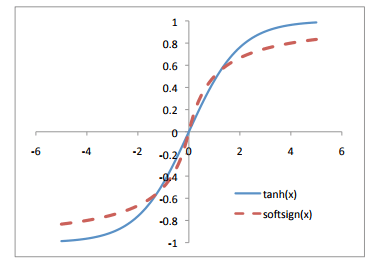
Tanh和softsign激活函数
我们在假设的100层网络中每一层添加双曲正切激活函数,然后观察使用我们的权重初始化方案时会发生什么,这里层的权重按(1 over sqrt{n})缩小。
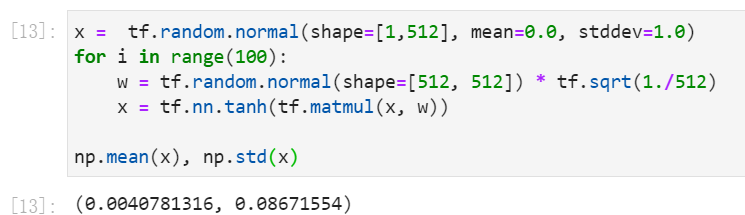
使用random.normal正态分布随机初始化,100次后输出
第100层的输出的标准差约为0.087,这个值是偏小的,但至少激活并没有完全消失!
现在回想起来,发现我们自己的权重初始化策略还是很直观的。但你可能会发现,就在2010年,这还不是初始化网络层权重的传统方法。当Xavier Glorot和Yoshua Bengio发表了他们的
标志性文章《Understanding the difficulty of training deep feedforward neural networks》,
他们在实验中对比的“启发式”方法是:使用[-1,1]的均匀分布来初始化权重,然后按(1 over sqrt{n})的比例缩放权重。事实证明,这种“标准”方法实际上并不能很好地发挥作用。
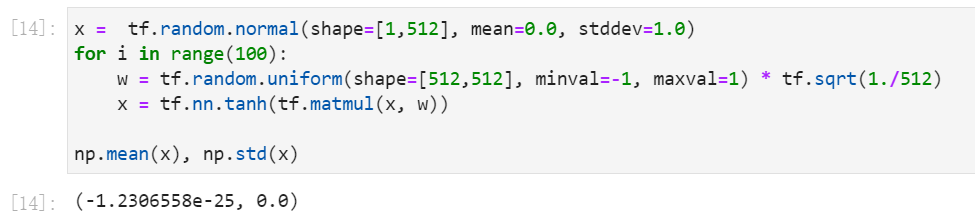
使用[-1,1)均匀分布来初始化,100次后输出消失
使用这种“标准”权重初始化方法重新运行我们的100层(tanh)网络会导致激活梯度变得无限小--就像消失了一样。
这种糟糕的结果促使Glorot和Bengio提出他们自己的权重初始化策略,他们在论文中称之为“normalized initialization”,现在通常被称为“Xavier初始化”。
Xavier初始化策略是使用以(pm sqrt{6} over {sqrt{n_i+n_{i+1}}})为边界的随机均匀分布对权重进行初始化。 其中(n_i)是输入数目("fan-in"),(n_{i+1})是输出数目("fan-out")。
Glorot和Bengio认为Xavier权重初始化将保持激活函数的前向传播的方差和梯度反向传播的方差。在实验中,他们观察到Xavier初始化使一个5层网络能够将每层的权重梯度维持在几乎同样的方差。

使用Xavier初始化
相反,若不使用Xavier初始化,而是直接使用“标准”初始化,会导致网络的下层权重梯度(较大)与最上层(接近零)的权重梯度之间的差异更大。
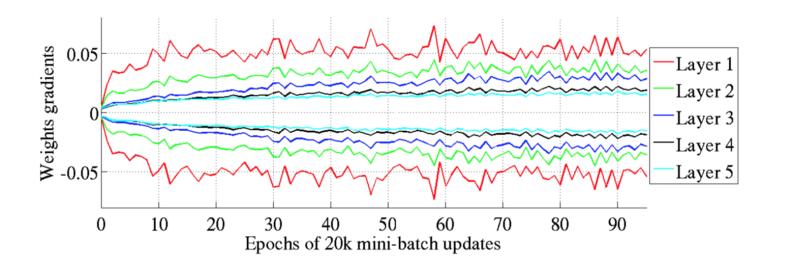
不使用Xavier初始化
重点就是,Glorot和Bengio证明了使用Xavier初始化的网络在CIFAR-10图像分类任务上实现了更快的收敛速度和更高的精度。
让我们再次重新运行我们的100层(tanh)网络,这次使用Xavier初始化:

使用Xavier初始化
在我们所做的实验中,Xavier初始化方法与我们之前自定义的方法非常相似,之前的方法是从随机正态分布中采样,并使用输入数目(n)的平方根进行缩放。
4. Kaiming初始化
理论上,当使用关于0对称并且在[-1,1]内有输出的激活函数(例如softsign和tanh)时,我们希望每层的输出平均值为0,平均标准差为1。这正是我们的自定义方法和Xavier都能实现的。
但是,如果我们使用(ReLU)激活函数呢?以同样的方式缩放初始权重值是否仍然有意义?

ReLU激活函数
为了弄明白会发生什么,让我们在先前假设的100层网络层中使用(ReLU)激活来代替(tanh),并观察其输出的标准差。

使用ReLU激活函数
事实证明,当使用(ReLU)激活时,单层的平均标准差非常接近输入数目的平方根除以2的平方根,在我们的例子中也就是(sqrt{512} over sqrt{2})。
使用该值缩放权重w将会导致每个(ReLU)层的输出具有1的标准差,如下例,

使用sqrt(2/512)缩放初始化权重
研究如何最优的初始化以(ReLU)为激活函数的网络的权重,何凯明提出他们自己的方案,专门用来处理这些非对称、非线性激活的深层神经网络。
在他们的2015年论文中何凯明等人证明了如果采用以下输入权重初始化策略,深层网络(例如22层CNN)会更快收敛:
-
创建合适的权重矩阵w,并使用标准正态分布随机初始化权重。
-
将每个随机选择的数字乘以(sqrt{2 over n}),其中(n)是前一层输出到本层的连接数目(也称为“fan-in”)。
-
偏差bias初始化为零。
我们可以按照这些指示来实现Kaiming初始化,并验证在100层网络所有层使用(ReLU),它确实可以防止输出爆炸或消失。

使用kaiming初始化,ReLU激活
最后再来对比,对所有层使用(ReLU)激活函数,但是用Xavier初始化,
使用Xavier初始化,ReLU激活
使用Xavier初始化,输出在第100非常接近0,几乎消失了。
当他们使用(ReLU)训练更深层的网络时,何凯明等人发现使用Xavier初始化的30层CNN完全停止并且不再学习。然而使用上面的He初始化相同的网络时,它的收敛效果非常好。

当我们从头开始训练的任何网络,特别是计算机视觉应用,几乎肯定会包含(ReLU)激活函数,并且是深度网络。在这种情况下,Kaiming初始化应该是我们首选的权重初始化策略。
-----------------------------------------------------------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------------------------
第1部分参考: https://towardsdatascience.com/weight-initialization-in-neural-networks-a-journey-from-the-basics-to-kaiming-954fb9b47c79
第2部分参考: