字符串匹配
转载,作者洛谷网校 阮行止
https://www.zhihu.com/question/21923021/answer/1032665486
前导
这里用到的数组下标都是从0开始的
1.思想
最朴素的算法就是一个一个地进行比较,但是有一种算法,它将信息运用到了极致,**它就是kmp
它最核心的思想就是尽可能利用残余的信息。**
2.优化
在** Brute-Force **中,如果从 S[i] 开始的那一趟比较失败了,算法会直接开始尝试从 S[i+1] 开始比
较。这种行为,属于典型的“没有从之前的错误中学到东西”。我们应当注意到,一次失败的匹配,会给
我们提供宝贵的信息——如果 S[i : i+len(P)] 与 P 的匹配是在第 r 个位置失败的,那么从 S[i] 开始的
(r-1) 个连续字符,一定与 P 的前 (r-1) 个字符一模一样!
3.跳过不可能成功的字符串比较
有些趟字符串比较是有可能会成功的;有些则毫无可能。我们刚刚提到过,优化 Brute-Force 的路线是“尽
量减少比较的趟数”,而如果我们跳过那些绝不可能成功的字符串比较,则可以希望复杂度降低到能接受的范
围。
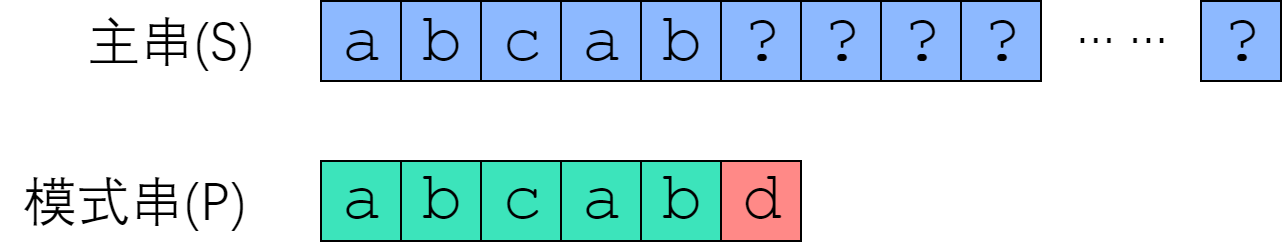
首先,利用上一节的结论。既然是在 P[5] 失配的,那么说明 S[0:5] 等于 P[0:5],即"abcab". 现在我
们来考虑:从 S[1]、S[2]、S[3] 开始的匹配尝试,有没有可能成功? 从 S[1] 开始肯定没办法成功,
因为 S[1] = P[1] = 'b',和 P[0] 并不相等。从 S[2] 开始也是没戏的,因为 S[2] = P[2] = 'c',
并不等于P[0]. 但是从 S[3] 开始是有可能成功的——至少按照已知的信息,我们推不出矛盾。

4.带着“跳过不可能成功的尝试”的思想,我们来看next数组。
next数组是对于模式串而言的,是要进行匹配的。P 的 next 数组定义为:next[i] 表示 P[0] ~
P[i] 这一个子串,使得 前k个字符恰等于后k个字符 的最大的k. 特别地,k不能取i+1(因为这个子串一共
才 i+1 个字符,自己肯定与自己相等,就没有意义了)。
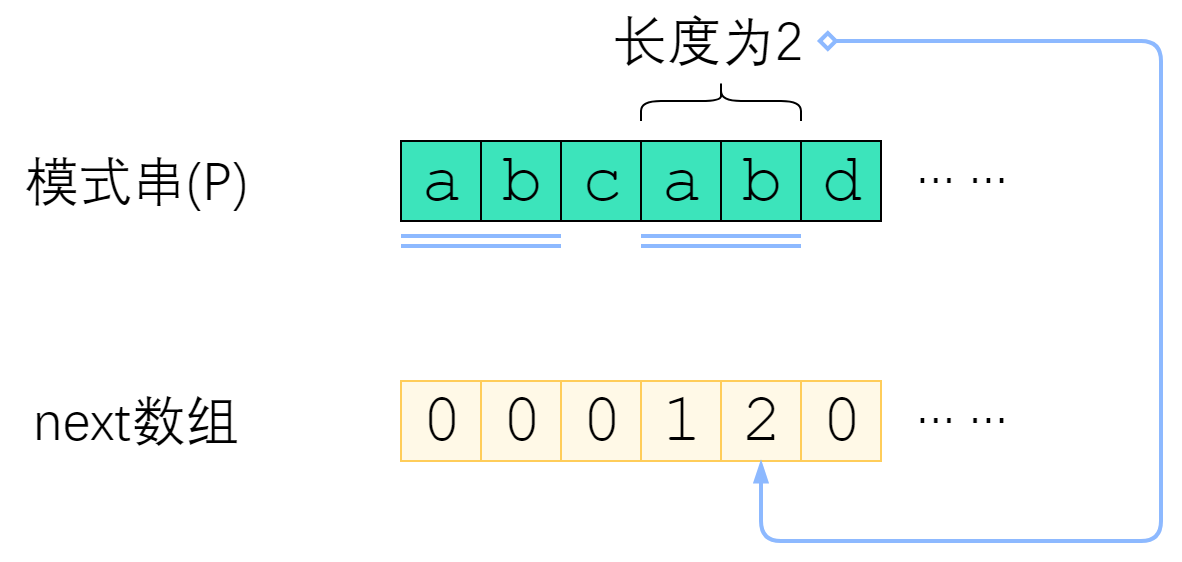
上图给出了一个例子。P="abcabd"时,next[4]=2,这是因为P[0] ~ P[4] 这个子串是"abcab",前两个字
符与后两个字符相等,因此next[4]取2. 而next[5]=0,是因为"abcabd"找不到前缀与后缀相同,因此只能
取0. 如果把模式串视为一把标尺,在主串上移动,那么 Brute-Force 就是每次失配之后只右移一位;
改进算法则是每次失配之后,移很多位,跳过那些不可能匹配成功的位置。但是该如何确定要移多少位呢?

在 S[0] 尝试匹配,失配于 S[3] <=> P[3] 之后,我们直接把模式串往右移了两位,让 S[3] 对准 P[1].
接着继续匹配,失配于 S[8] <=> P[6], 接下来我们把 P 往右平移了三位,把 S[8] 对准 P[3]. 此后继
续匹配直到成功。 我们应该如何移动这把标尺?很明显,如图中蓝色箭头所示,旧的后缀要与新的前缀一
致(如果不一致,那就肯定没法匹配上了)! 回忆next数组的性质:P[0] 到 P[i] 这一段子串中,前
next[i]个字符与后next[i]个字符一模一样。既然如此,如果失配在 P[r], 那么P[0]~P[r-1]这一段里
面,前next[r-1]个字符恰好和后next[r-1]个字符相等——也就是说,我们可以拿长度为 next[r-1] 的那一
段前缀,来顶替当前后缀的位置,让匹配继续下去! 您可以验证一下上面的匹配例子:P[3]失配后,把
P[next[3-1]]也就是P[1]对准了主串刚刚失配的那一位;P[6]失配后,把P[next[6-1]]也就是P[3]对准了
主串刚刚失配的那一位。

如上图所示,绿色部分是成功匹配,失配于红色部分。深绿色手绘线条标出了相等的前缀和后缀,其长度为
next[右端]. 由于手绘线条部分的字符是一样的,所以直接把前面那条移到后面那条的位置。因此说,next
数组为我们如何移动标尺提供了依据。接下来,我们实现这个优化的算法。
利用next数组进行匹配
了解了利用next数组加速字符串匹配的原理,我们接下来代码实现之。分为两个部分:建立next数组、
利用next数组进行匹配。
首先是建立next数组。我们暂且用最朴素的做法,以后再回来优化:
void calc_next()
{
next[1]=0;
for(int i=2,j=0;i<=n;i++)
{
while(j>0&&a[i]!=a[j+1])
j=next[j];
if(a[i]==a[j+1])
j++,next[j]=j;
}
}
快速求next数组 终于来到了我们最后一个问题——如何快速构建next数组。 首先说一句:快速构建
next数组,是KMP算法的精髓所在,核心思想是“P自己与自己做匹配”。 为什么这样说呢?回顾next数组
的完整定义:定义 “k-前缀” 为一个字符串的前 k 个字符; “k-后缀” 为一个字符串的后 k 个字符。k 必
须小于字符串长度。 next[x] 定义为: P[0]~P[x] 这一段字符串,使得k-前缀恰等于k-后缀的最大的
k. 这个定义中,不知不觉地就包含了一个匹配——前缀和后缀相等。接下来,我们考虑采用递推的方式求出
next数组。如果next[0], next[1], ... next[x-1]均已知,那么如何求出 next[x] 呢? 来分情况讨
论。首先,已经知道了 next[x-1](以下记为now),如果 P[x] 与 P[now] 一样,那最长相等前后缀的长
度就可以扩展一位,很明显 next[x] = now + 1. 图示如下。
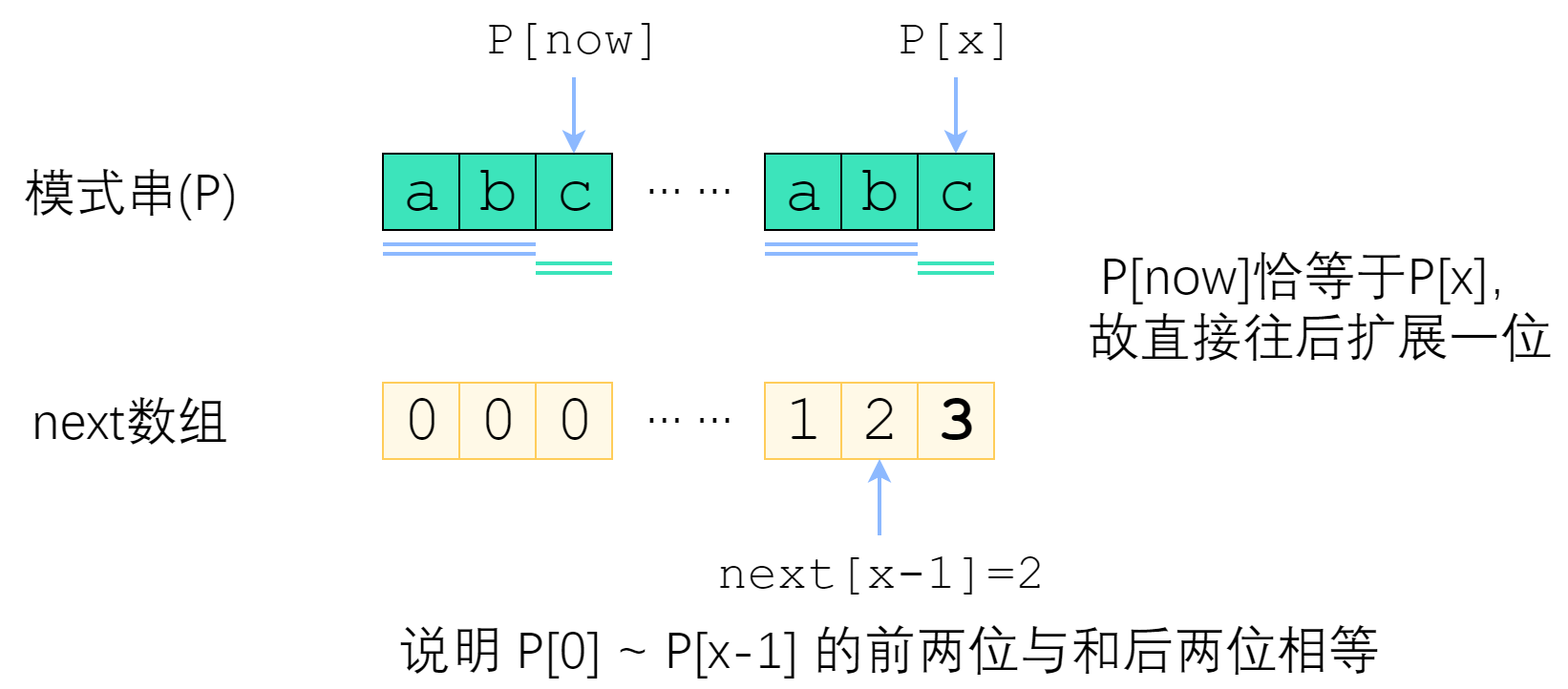
刚刚解决了 P[x] = P[now] 的情况。那如果 P[x] 与 P[now] 不一样,又该怎么办?

如图。长度为 now 的子串 A 和子串 B 是 P[0]~P[x-1] 中最长的公共前后缀。可惜 A 右边的字符和 B 右边的那个字符不相等,next[x]不能改成 now+1 了。因此,我们应该缩短这个now,把它改成小一点的值,再来试试 P[x] 是否等于
P[now]. now该缩小到多少呢?显然,我们不想让now缩小太多。因此我们决定,在保持“P[0]~P[x-1]的now-前缀仍然等于now-后缀”的前提下,让这个新的now尽可能大一点。 P[0]~P[x-1] 的公共前后缀,前缀一定落在串A里面、后缀一定落
在串B里面。换句话讲:接下来now应该改成:使得 A的k-前缀等于B的k-后缀 的最大的k. 您应该已经注意到了一个非常强的性质——串A和串B是相同的!B的后缀等于A的后缀!因此,使得A的k-前缀等于B的k-后缀的最大的k,其实就是串A的最长
公共前后缀的长度 —— next[now-1]!

来看上面的例子。当P[now]与P[x]不相等的时候,我们需要缩小now——把now变成next[now-1],直到P[now]=P[x]为止。P[now]=P[x]时,就可以直接向右扩展了。