Java课程作业02

课后作业3

1.设计思想

输入字串利用递归函数进行循环判断字串的各个位置的字符是否相等

2.程序流程图

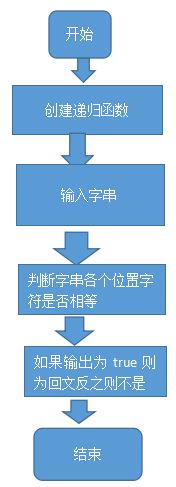
3.源代码

import java.util.Scanner;

public class huiwen {

public static boolean isPalindrome(String s,int i,int j){

     

        if(i == j)

            return true;

        else{

            return (s.charAt(i) == s.charAt(j)) && isPalindrome(s,i+1,j-1);

        }

}

public static void main(String[] args) {

// TODO Auto-generated method stub

  Scanner scanner=new Scanner(System.in);

        String s = scanner.nextLine();

        int i = 0;

        int j = s.length() - 1;

        if(huiwen.isPalindrome(s,i,j))

         System.out.println(s+" 是回文字串");

         else

         System.out.println(s+" 不是回文字串");

}

}

4.结果截图

课后作业2

1.设计思想

思路：将n个圆盘从柱子1移动到柱子3，按照大的圆盘在最下面的顺序依次往上堆放，每一步只能把某个柱子最上面的一个圆盘移到另一个柱子上面，要解决这个问题，由于要把圆盘从柱子1移到柱子3，必须先将最大的盘子移动到柱子3。要达到这个目的此前柱子3必须是空的，而且柱子1上只能有最大的圆盘，因此其余的n-1个圆盘只能在柱子2上。假设函数move能把柱子1上的n-1个圆盘移动到柱子2，并将柱子1上最下面（最大）的圆盘移动到柱子3，那么最后只需再利用move，将柱子2上的n-1个圆盘移动到柱子3就能完成任务了。

2.程序流程图

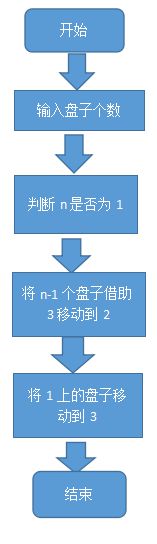
3.源代码

import java.util.*;

public class hannuota {
public static void tower(int n,char one,char two,char three){
if(n==1)
{
move(one,three,1);
}
else
{
tower(n-1,one,three,two);
move(one,three, n);
tower(n-1,two,one,three);
}
}
//输出
public static void move(char x,char y, int n){
System.out.println(x+"的第"+n+"盘移动到"+y);
}
public static void main(String[] args){
int n;
Scanner in = new Scanner(System.in);
System.out.println("请输入盘子个数：");
n = in.nextInt();
hannuota.tower(n,'A','B','C');
}
}

4.结果截图

课后作业1

1.设计思路

使用组合数公式利用n!来计算

使用递推的方法用杨辉三角形计算

2.程序流程图

 

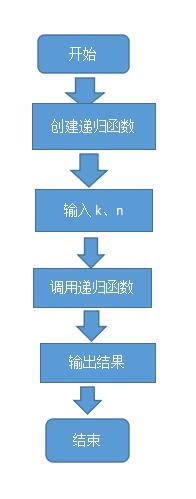
3.源代码

import java.util.*;
import javax.swing.JOptionPane;
public class jiecheng {
public static long fact(int k,int n){
if(k==0||n==0)
return 1;
if(n<k)
return 0;
if(n==k)
return 1;
return fact(k-1,n-1)+fact(k,n-1);
}
public static long jiecheng(int i){
if(i==1||i==0)
return 1;
else
return i*jiecheng(i-1);

}
public static void main(String[] args){
String n1,n2;
int i,j;
Scanner input=new Scanner(System.in);
n1=JOptionPane.showInputDialog( "输入k的值：" );
n2=JOptionPane.showInputDialog( "输入n的值：" );
i= Integer.parseInt(n1);
j= Integer.parseInt(n2);
JOptionPane.showMessageDialog(
null,"利用阶乘计算：" +jiecheng(j)/(jiecheng(i)*jiecheng(j-i)));
JOptionPane.showMessageDialog(
null,"利用杨辉三角计算：" +fact(i,j));
}
}

4.结果截图