1、第一个题:最近邻居
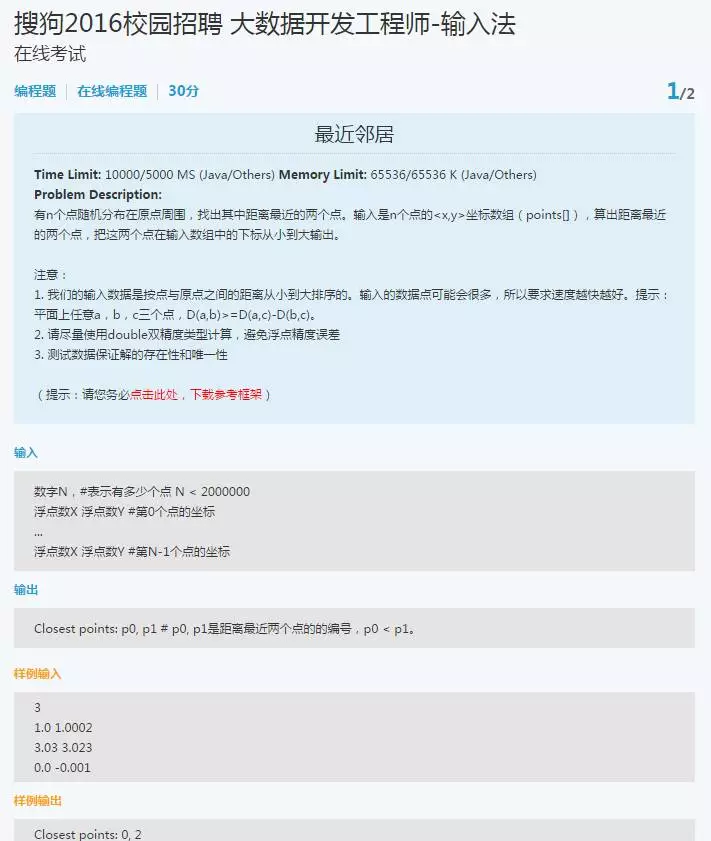
题目:
解题思路:
1)这个题如果用java,相对会好解一些,因为可以直接用JDK中的Point2D类,来定义坐标系空间中的一个点。
2)简单思路:暴力破解,计算任意两个点之间的距离,时间负责度为O(n^2);
3)优化思路:《编程之美》上给出了一个思路,利用分治法,将所有点所在的平面切成点数大致相同的两半,分为Left,Right,则距离最近的两个点,要么在Left区域中,要么在Right区域中,要么在跨两者中间的区域中,时间复杂度可以优化到O(nlgn)。下面给出暴力破解的C++实现。
考察:二维平面求距离,库函数的应用,算法优化。
1 struct Point2D{ 2 double x; 3 double y; 4 Point2D(double x1=0.0, double y1=0.0):x(x1),y(y1) {} 5 }; 6 7 int* ClosetNeighborOfPoint2D(Point2D *pPoint, int n) 8 { 9 if (NULL == pPoint || n < 2) 10 return NULL; 11 12 double minDistance = DBL_MAX; //"float.h, limits.h" 13 int *pRet = new int[2]; 14 15 for (int i = 0; i < n-1; i ++) { 16 for (int j = i + 1; j < n; j ++) { 17 double temp = pow(pPoint[j].x-pPoint[i].x,2)+pow(pPoint[j].y-pPoint[i].y, 2); 18 19 if (temp < minDistance) { 20 minDistance = temp; 21 pRet[0] = i; 22 pRet[1] = j; 23 } 24 } 25 } 26 if (pRet[0] > pRet[1]) { 27 int t = pRet[0]; 28 pRet[0] = pRet[1]; 29 pRet[1] = t; 30 } 31 return pRet; 32 }
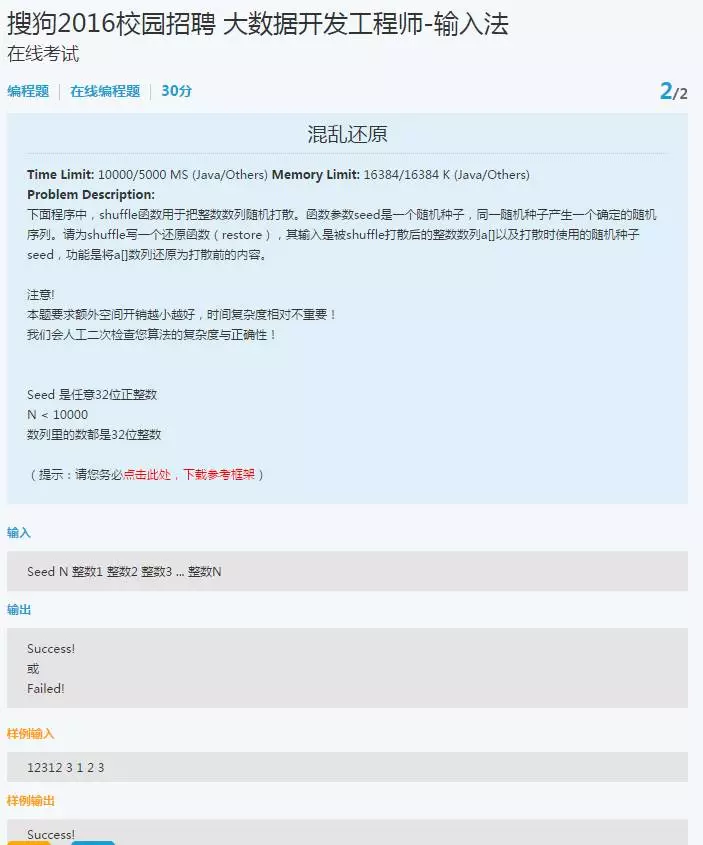
2、第二个题:混乱还原
题目:
解题思路:
1)利用伪随机特性,只要时间种子一样且上限一样,都会产生相同的随机数;
2)保证打乱的序列能被还原,则需要一个额外的栈来保存随机数,把打乱所使用的随机数出栈与对应的元素进行交换就可以恢复。
考察:随机数的应用,栈的应用。
1 void ShufferPhase(vector<int> &ivec, int seed) 2 { 3 if (ivec.size() == 0 || seed <= 0) 4 return; 5 int n = ivec.size(); 6 7 srand(seed); 8 for (int i = n; i > 0; i --) { 9 int r = rand()%i; 10 int t = ivec[i-1]; 11 ivec[i-1] = ivec[r]; 12 ivec[r] = t; 13 } 14 } 15 16 void ReStorePhase(vector<int> &ivec, int seed) 17 { 18 if (ivec.size() == 0 || seed <= 0) 19 return; 20 21 int n = ivec.size(); 22 stack<int> istack; 23 24 srand(seed); 25 for (int i = n; i > 0; i --) { 26 int r = rand()%i; 27 istack.push(r); 28 } 29 30 for (int i = 0; i < n; i ++) { 31 int r = istack.top(); 32 istack.pop(); 33 int t = ivec[r]; 34 ivec[r] = ivec[i]; 35 ivec[i] = t; 36 } 37 }