二叉查找树
它或者是一棵空树;或者是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(2)若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(3)左、右子树也分别为二叉排序树
创建二叉查找树
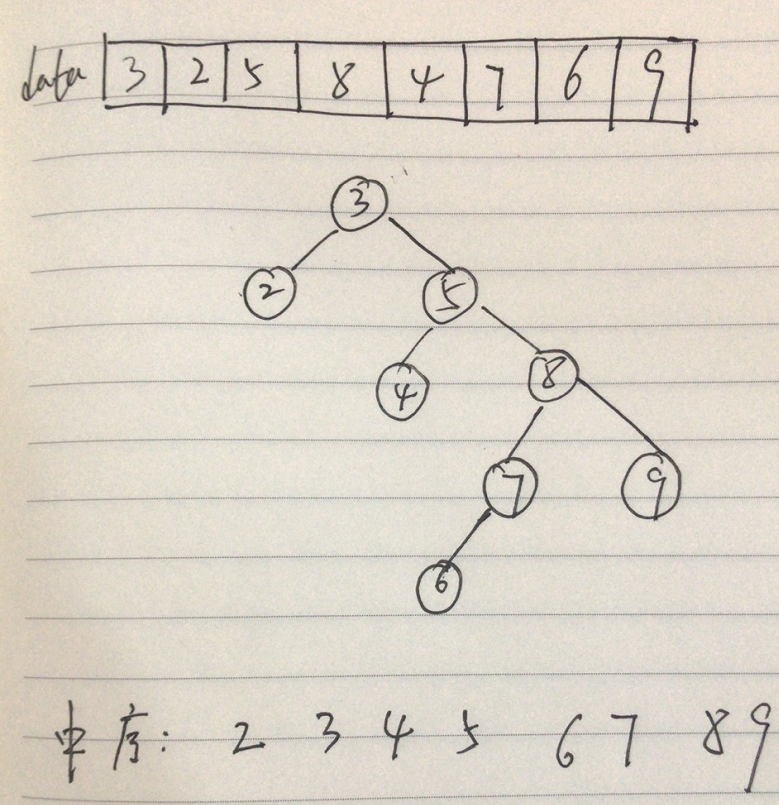
#include<stdio.h> #include<stdlib.h> typedef struct node{ int value; struct node *lchild,*rchild,*parent; }TreeNode; //create Tree TreeNode * createTree(int data[],int n){ TreeNode *root =NULL,*p,*pre=NULL,*tag=NULL; int i; for(i=0;i<n;i++){ p = (TreeNode *)malloc(sizeof(TreeNode)); p->value=data[i]; p->lchild=p->rchild=p->parent = NULL; if(root==NULL){ root = p; }else{ tag = root; for(pre=root;pre!=NULL&&p->value<pre->value;tag=pre,pre=pre->lchild); for(;pre!=NULL&&p->value>=pre->value;tag=pre,pre=pre->rchild); if(pre!=NULL) tag = pre; if(p->value<tag->value){ tag->lchild = p; p->parent = tag; }else{ tag->rchild = p; p->parent = tag; } } } return root; } //print void print(TreeNode *root){ if(root->lchild!=NULL){ print(root->lchild); } printf("[lchild]:%8d [value]:%5d [root]:%8d [rchild]:%8d [parent]:%8d ",root->lchild,root->value,root,root->rchild,root->parent); if(root->rchild!=NULL){ print(root->rchild); } } int main(void){ int data[8] = {3,2,5,8,4,7,6,9}; //createTree TreeNode *root = createTree(data,8); print(root); return 0; }
完整代码
#include<stdio.h> #include<stdlib.h> typedef struct node{ int value; struct node *lchild,*rchild,*parent; }TreeNode; //create Tree TreeNode * createTree(int data[],int n){ TreeNode *root =NULL,*p,*pre=NULL,*tag=NULL; int i; for(i=0;i<n;i++){ p = (TreeNode *)malloc(sizeof(TreeNode)); p->value=data[i]; p->lchild=p->rchild=p->parent = NULL; if(root==NULL){ root = p; }else{ tag = root; for(pre=root;pre!=NULL&&p->value<pre->value;tag=pre,pre=pre->lchild); for(;pre!=NULL&&p->value>=pre->value;tag=pre,pre=pre->rchild); if(pre!=NULL) tag = pre; if(p->value<tag->value){ tag->lchild = p; p->parent = tag; }else{ tag->rchild = p; p->parent = tag; } } } return root; } //print void print(TreeNode *root){ if(root->lchild!=NULL){ print(root->lchild); } printf("[lchild]:%8d [value]:%5d [root]:%8d [rchild]:%8d [parent]:%8d ",root->lchild,root->value,root,root->rchild,root->parent); if(root->rchild!=NULL){ print(root->rchild); } } int main(void){ int data[8] = {3,2,5,8,4,7,6,9}; //createTree TreeNode *root = createTree(data,8); print(root); return 0; }
