红黑树
一、红黑树性质
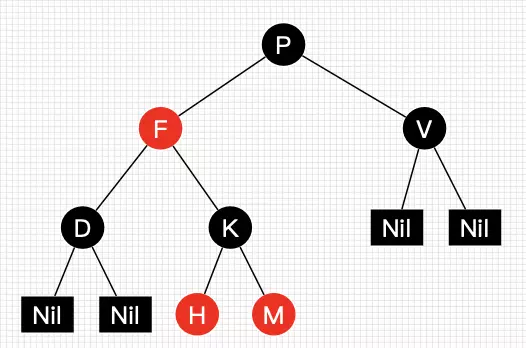
- 每个节点的颜色是红色或者黑色
- 根节点是黑色
- 每个叶子节点是黑色
- 每个红色节点的2个子节点一定是黑色
- 任意一节点出发到每个叶子节点的路径都包含相同数量的黑节点 (因此是 黑色完美平衡二叉树)
红黑树不是一个完美平衡二叉树,但从性质 5 可以总结红黑树是黑色完美平衡
二、红黑树节点
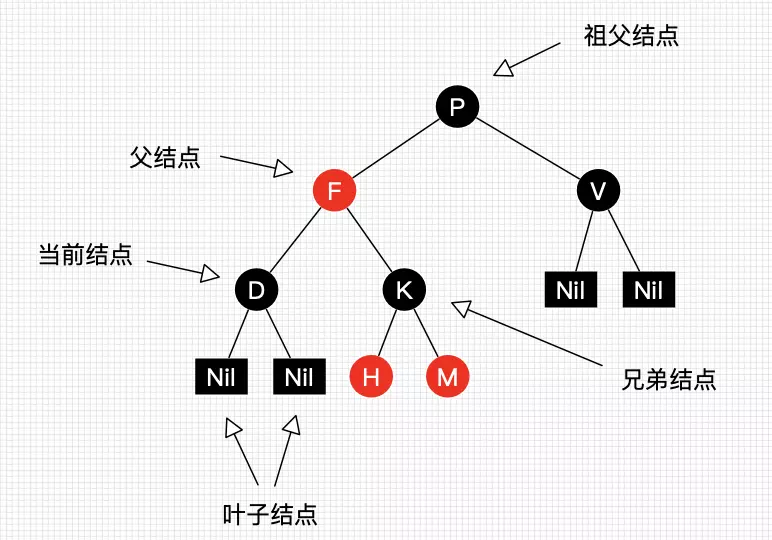
我们把正在处理遍历的节点叫做当前节点如上图的D ,当前节点的上级节点叫父节点,其父亲的另一个子节点叫做兄弟节点,父节点的父节点叫祖父节点。祖父节点的另一个子节点叫叔叔节点
红黑树能够自平衡的依靠 ,三种操作:左旋、右旋、变色
左旋:以某个节点为支点(旋转节点),其右子节点变为旋转节点的父节点,右子节点的左子节点变为旋转节点的右子节点
右旋:以某个节点作为支点/旋转节点,其左子节点变为旋转节点的父节点,左子节点的右子节点变为旋转节点的左子节点,右子节点保持不变
变色:节点的颜色由红变黑或者由黑变红
左旋操作
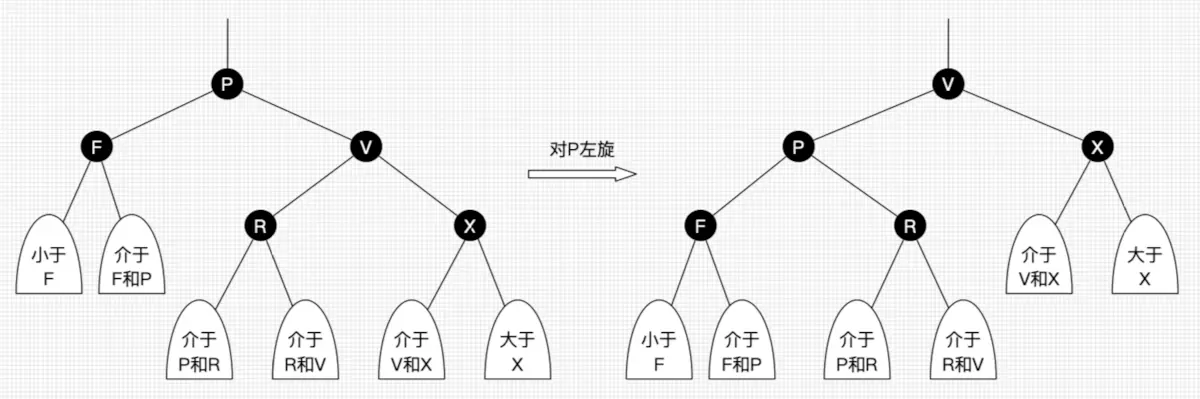
右旋操作

旋转操作是局部的,红黑树总是通过旋转和变色来达到自平衡
扩展:红色节点的父节点一定是黑色的
三、红黑树插入节点
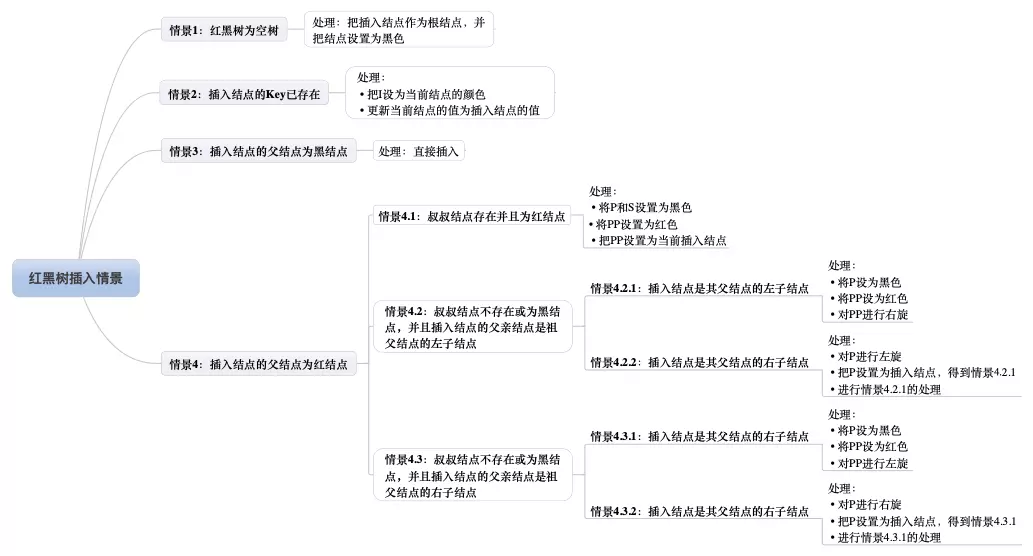
红黑树插入的 八种场景分析,首先对节点进行约定
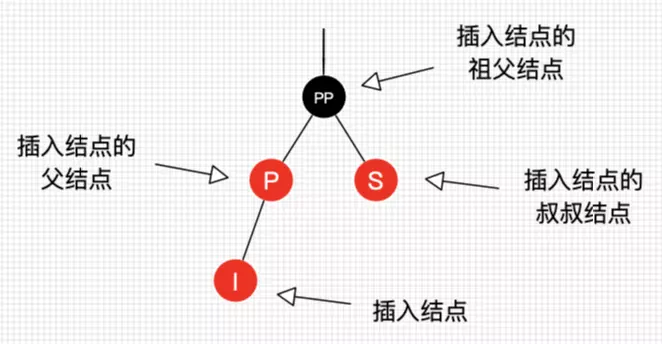
这是一种简单的情景,直接把插入节点作为根节点,但是要注意根节点是黑色的,需要变色
插入节点是红色的,父节点是黑色的,可以直接插入,无需自平衡
该父节点不可能为根节点,所以插入节点总有祖父节点,所以分多种情况
根据性值推断,祖父节点一定为黑节点,此时情况是 黑红红,最简单的处理如下
- 将 P 和 S 设置为黑色
- 将 PP 设置为红色
- 把 PP 设置为当前插入节点
左节点增加

右节点增加

如果设置 PP 节点为红色,如果 PP 节点父节点是黑色,则无需处理。如果 PP 节点的父节点是红色,那么红黑树不再平衡,所以把PP 当作插入节点继续当插入节点做自平衡,直到平衡为止。
红黑树的生长是自低向上的,而普通的二叉树是自顶向下的。
因为叔叔节点为黑节点,而父亲节点为红节点
- 将 P 设为黑色
- 将 PP 设为红色
- 对 PP 进行右旋

当然,可以把 P 设为红色, I 和 PP 设为黑色,也是可以的,但是需要自底向上处理,多做多余的处理,既然能消化就不要麻烦祖辈们
3.6 父节点红,叔叔不存在,插入节点是其父节点的右子节点
- 对 P 进行左旋
- 把 P 设置为插入节点
- 进行上述处理
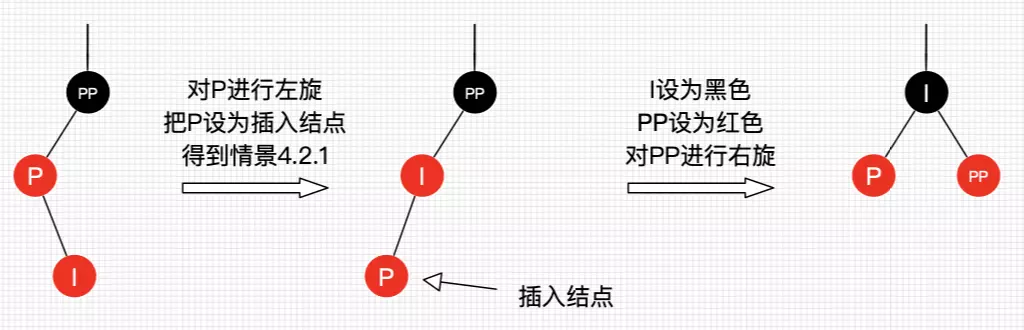
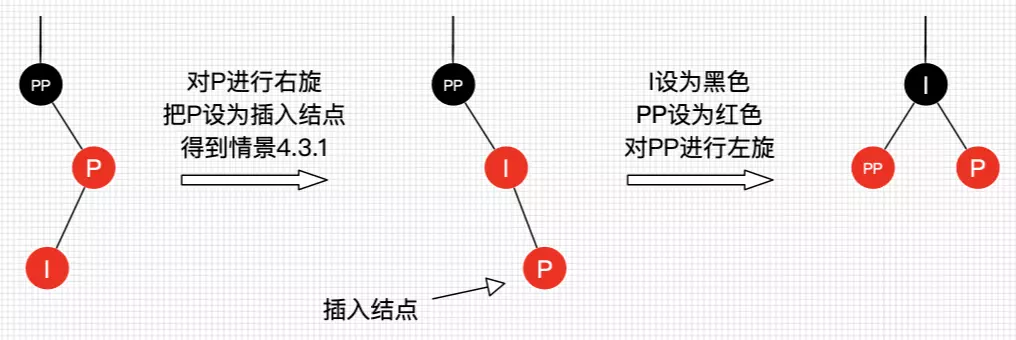
3.7 叔叔节点不存在或者为黑节点,并且插入节点的父亲节点是祖父节点的右子节点
与上述方向相反
- 将 P 设为 黑色
- 将 PP 设为红色】
- 对 PP 进行左旋

#include <stdio.h> #include <stdlib.h> const int RED = 0; const int BLACK = 1; typedef struct rb_node{ struct rb_node* lchild, *rchild, *parent; int key, colour; }rb_node; rb_node* root; rb_node* get_node(rb_node* parent, int key); void rb_insert(int key); rb_node* rb_search(int key); void rb_delete(int key); rb_node* clock_wise(rb_node* node); rb_node* counter_clock_wise(rb_node* node); void show_rb_tree(rb_node* node); rb_node* get_node(rb_node* parent, int key){ rb_node *tmp = (rb_node*)malloc(sizeof(rb_node)); tmp->key = key; tmp->colour = RED; tmp->parent = parent; tmp->lchild = tmp->rchild = NULL; return tmp; } rb_node* clock_wise(rb_node* node){ if(node == NULL || node->lchild == NULL) return NULL; rb_node *rb_1=node, *rb_2=node->lchild, *rb_3=node->lchild->rchild; if(rb_1->parent != NULL){ if(rb_1->parent->lchild == rb_1) rb_1->parent->lchild = rb_2; else rb_1->parent->rchild = rb_2; }else if(rb_1 == root){ root = rb_2; } rb_2->parent = rb_1->parent; rb_1->parent = rb_2; rb_2->rchild = rb_1; rb_1->lchild = rb_3; if(rb_3 != NULL)rb_3->parent = rb_1; return rb_2; } rb_node* counter_clock_wise(rb_node* node){ if(node == NULL || node->rchild == NULL) return NULL; rb_node *rb_1=node, *rb_2=node->rchild, *rb_3=node->rchild->lchild; if(rb_1->parent != NULL){ if(rb_1->parent->lchild == rb_1) rb_1->parent->lchild = rb_2; else rb_1->parent->rchild = rb_2; } else if(rb_1 == root){ root = rb_2; } rb_2->parent = rb_1->parent; rb_1->parent = rb_2; rb_2->lchild = rb_1; rb_1->rchild = rb_3; if(rb_3 != NULL)rb_3->parent = rb_1; return rb_2; } rb_node* rb_search(int key){ rb_node *p = root; while(p != NULL){ if(key < p->key) p = p->lchild; else if(key > p->key) p = p->rchild; else break; } return p; } void rb_insert(int key){ rb_node *p=root, *q=NULL; if(root == NULL){ root = get_node(NULL, key); root->colour = BLACK; return; } while(p != NULL){ q = p; if(key < p->key) p = p->lchild; else if(key > p->key) p = p->rchild; else return; } if(key < q->key) q->lchild = get_node(q, key); else q->rchild = get_node(q, key); while(q != NULL && q->colour == RED){ p = q->parent;//p won't null, or BUG. if(p->lchild == q){ if(q->rchild != NULL && q->rchild->colour == RED) counter_clock_wise(q); q = clock_wise(p); q->lchild->colour = BLACK; } else{ if(q->lchild != NULL && q->lchild->colour == RED) clock_wise(q); q = counter_clock_wise(p); q->rchild->colour = BLACK; } q = q->parent; } root->colour = BLACK; } void show_rb_tree(rb_node* node){ if(node == NULL) return; // printf("(%3d,%3d) ", node->key, node->colour); // if(node->lchild != NULL){ // printf("[-1] "); // show_rb_tree(node->lchild); // } // if(node->rchild != NULL){ // printf("[1] "); // show_rb_tree(node->rchild); // } // printf("[0] "); show_rb_tree(node->lchild); printf("%3d",node->key); show_rb_tree(node->rchild); } void rb_delete(int key){ rb_node *v = rb_search(key), *u, *p, *c, *b; int tmp; if(v == NULL) return; u = v; if(v->lchild != NULL && v->rchild != NULL){ u = v->rchild; while(u->lchild != NULL){ u = u->lchild; } tmp = u->key; u->key = v->key; v->key = tmp; } //u is the node to free. if(u->lchild != NULL) c = u->lchild; else c = u->rchild; p = u->parent; if(p != NULL){ //remove u from rb_tree. if(p->lchild == u) p->lchild = c; else p->rchild = c; } else{ //u is root. root = c; free((void*)u); return; } //u is not root and u is RED, this will not unbalance. if(u->colour == RED){ free((void*)u); return; } free((void*)u); u = c; //u is the first node to balance. while(u != root){ if(u != NULL && u->colour == RED){ //if u is RED, change it to BLACK can finsh. u->colour = BLACK; return; } if(u == p->lchild) b = p->rchild; else b = p->lchild; printf("%d ", b->key); //b is borther of u. b can't be null, or the rb_tree is must not balance. if(b->colour == BLACK){ //If b's son is RED, rotate the node. if(b->lchild != NULL && b->lchild->colour == RED){ if(u == p->lchild){ b = clock_wise(b); b->colour = BLACK; b->rchild->colour = RED; p = counter_clock_wise(p); p->colour = p->lchild->colour; p->lchild->colour = BLACK; p->rchild->colour = BLACK; } else{ p = clock_wise(p); p->colour = p->rchild->colour; p->rchild->colour = BLACK; p->lchild->colour = BLACK; } return; } else if(b->rchild != NULL && b->rchild->colour == RED){ if(u == p->rchild){ b = counter_clock_wise(b); b->colour = BLACK; b->lchild->colour = RED; p = clock_wise(p); p->colour = p->rchild->colour; p->rchild->colour = BLACK; p->lchild->colour = BLACK; } else{ p = counter_clock_wise(p); p->colour = p->lchild->colour; p->lchild->colour = BLACK; p->rchild->colour = BLACK; } return; } else{//if b's sons are BLACK, make b RED and move up u. b->colour = RED; u = p; p = u->parent; continue; } } else{ if(u == p->lchild){ p = counter_clock_wise(p); p->colour = BLACK; p->lchild->colour = RED; p = p->lchild; } else{ p = clock_wise(p); p->colour = BLACK; p->rchild->colour = RED; p = p->rchild; } } } root->colour = BLACK; } int main(){ int i; root = NULL; rb_insert(3); rb_insert(2); rb_insert(5); rb_insert(8); rb_insert(4); rb_insert(7); rb_insert(6); rb_insert(9); // rb_delete(2); // rb_delete(5); // rb_delete(8); show_rb_tree(root); printf(" "); return 0; }
#include<stdio.h> #include<stdlib.h> typedef struct node{ int key; struct node *left,*right,*parent; int color; }TreeNode; const int BLACK = 1; const int RED = 0; TreeNode *root = NULL; //函数声明 TreeNode* newNode(TreeNode *parent,int key); //创建新的节点 TreeNode* newNode(TreeNode *parent,int key){ TreeNode *temp = (TreeNode *)malloc(sizeof(TreeNode)); temp->color = RED; temp->left = temp->right = NULL; temp->parent = parent; temp->key = key; return temp; } //子节点在右 TreeNode* isRight(TreeNode *node){ if(node == NULL || node->right ==NULL){ return NULL; } TreeNode *p1 = node,*p2 = node->right,*p3 = node->right->left; if(p1->parent!=NULL){ if(p1->parent->left = p1){ p1->parent->left = p2; }else{ p1->parent->right = p2; } }else if(p1 == root){ root = p2; } p2->parent = p1->parent; p1->parent = p2; p2->left = p1; p1->right = p3; if(p3!=NULL){ p3->parent = p1; } return p2; } //子节点在左 TreeNode* isLeft(TreeNode *node){ if(node == NULL || node->left ==NULL){ return NULL; } TreeNode *p1 = node,*p2 = node->left,*p3 = node->left->right; if(p1->parent!=NULL){ if(p1->parent->left == p1){ p1->parent->left = p2; }else{ p1->parent->right = p2; } }else if(p1 == root){ root = p2; } p2->parent = p1->parent; p1->parent = p2; p2->right = p1; p1->left = p3; if(p3!=NULL){ p3->parent = p1; } return p2; } void insertNode(int key){ TreeNode *p = root,*q = NULL; if(root == NULL){ //创建新节点 root = newNode(NULL,key); root->color = BLACK; return; } while(p!=NULL){ q = p; if(key<p->key){ p = p->left; }else if(key > p->key){ p = p->right; }else{ return; } } if(key<q->key){ q->left = newNode(q,key); }else{ q->right = newNode(q,key); } while(q!=NULL && q->color == RED){ p = q->parent; if(p->left == q){ if(q->right!=NULL&&q->right->color ==RED) isRight(q); q = isLeft(p); q->left->color = BLACK; }else{ if(q->left!=NULL&&q->left->color == RED) isLeft(q); q = isRight(p); q->right->color = BLACK; } q = q->parent; } root->color = BLACK; } //输出 void print(TreeNode *root){ if(root==NULL) return; print(root->left); printf("color:%3d root:%8d parent:%8d key:%d ",root->color,root,root->parent,root->key); print(root->right); } int main(void){ //插入 root =NULL; insertNode(3); insertNode(2); insertNode(5); insertNode(8); insertNode(4); insertNode(7); insertNode(6); insertNode(6); print(root); return 0; }
参考:https://www.jianshu.com/p/e136ec79235c