鉴于单峰的状态分布公式是:
f(x)=(1/((2π)^0.5)*σ)exp-((x-a)^2/(2*σ^2))
于是N个平均值。标准差值不同的正态分布公式应当是
f(x)= ∑(ki/((2π)^0.5)*σi)exp-((x-ai)^2/(2*σi^2))
以上求和是针对i的。这里每个i对应一个独立的平均值ai、标准差σi,以及它的概率峰位置,而各个ki是一个系数,并且它们的合计值=1.
显然以上函数对自变量x的积分=1.所以它符合概率密度函数的自然要求。
以下是代码
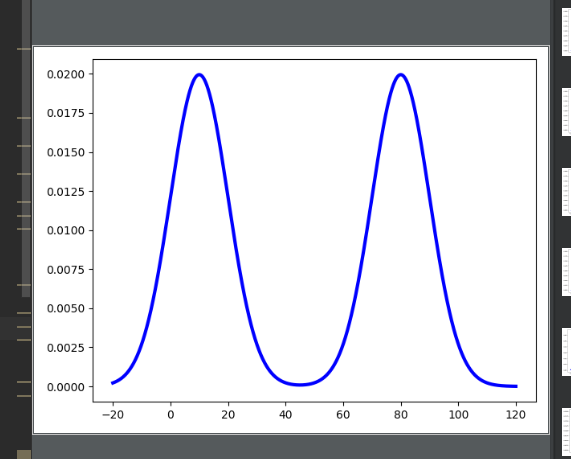
import numpy as np import matplotlib.pyplot as plt class TwoNomal(): def __init__(self,mu1,mu2,sigma1,sigma2): self.mu1 = mu1 self.sigma1 = sigma1 self.mu2 = mu2 self.sigma2 = sigma2 def doubledensity(self,x): mu1 = self.mu1 sigma1 = self.sigma1 mu2 = self.mu2 sigma2 = self.sigma1 N1 = np.sqrt(2 * np.pi * np.power(sigma1, 2)) fac1 = np.power(x - mu1, 2) / np.power(sigma1, 2) density1=np.exp(-fac1/2)/N1 N2 = np.sqrt(2 * np.pi * np.power(sigma2, 2)) fac2 = np.power(x - mu2, 2) / np.power(sigma2, 2) density2=np.exp(-fac2/2)/N2 #print(density1,density2) density=0.5*density2+0.5*density1 return density N2 = TwoNomal(10,80,10,10) #创建等差数列作为X X = np.arange(-20,120,0.05) #print(X) Y = N2.doubledensity(X) #print(Y) plt.plot(X,Y,'b-',linewidth=3) plt.show()