Pearson(皮尔逊)相关系数及MATLAB实现

转自：http://blog.csdn.net/wsywl/article/details/5727327

由于使用的统计相关系数比较频繁，所以这里就利用几篇文章简单介绍一下这些系数。

相关系数：考察两个事物（在数据里我们称之为变量）之间的相关程度。

如果有两个变量：X、Y，最终计算出的相关系数的含义可以有如下理解：

(1)、当相关系数为0时，X和Y两变量无关系。

(2)、当X的值增大（减小），Y值增大（减小），两个变量为正相关，相关系数在0.00与1.00之间。

(3)、当X的值增大（减小），Y值减小（增大），两个变量为负相关，相关系数在-1.00与0.00之间。

相关系数的绝对值越大，相关性越强，相关系数越接近于1或-1，相关度越强，相关系数越接近于0，相关度越弱。

通常情况下通过以下取值范围判断变量的相关强度：
相关系数     0.8-1.0     极强相关
                 0.6-0.8     强相关
                 0.4-0.6     中等程度相关
                 0.2-0.4     弱相关
                 0.0-0.2     极弱相关或无相关

Pearson（皮尔逊）相关系数

1、简介

皮尔逊相关也称为积差相关（或积矩相关）是英国统计学家皮尔逊于20世纪提出的一种计算直线相关的方法。

假设有两个变量X、Y，那么两变量间的皮尔逊相关系数可通过以下公式计算：

公式一：

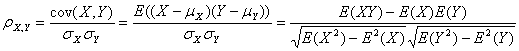
公式二：

公式三：

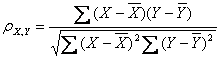
公式四：

以上列出的四个公式等价，其中E是数学期望，cov表示协方差，N表示变量取值的个数。

2、适用范围

当两个变量的标准差都不为零时，相关系数才有定义，皮尔逊相关系数适用于：

(1)、两个变量之间是线性关系，都是连续数据。

(2)、两个变量的总体是正态分布，或接近正态的单峰分布。

(3)、两个变量的观测值是成对的，每对观测值之间相互独立。

3、Matlab实现

皮尔逊相关系数的Matlab实现（依据公式四实现）：

function coeff = myPearson(X , Y)
% 本函数实现了皮尔逊相关系数的计算操作
%
% 输入：
%   X：输入的数值序列
%   Y：输入的数值序列
%
% 输出：
%   coeff：两个输入数值序列X，Y的相关系数
%


if length(X) ~= length(Y)
    error('两个数值数列的维数不相等');
    return;
end

fenzi = sum(X .* Y) - (sum(X) * sum(Y)) / length(X);
fenmu = sqrt((sum(X .^2) - sum(X)^2 / length(X)) * (sum(Y .^2) - sum(Y)^2 / length(X)));
coeff = fenzi / fenmu;

end %函数myPearson结束

也可以使用Matlab中已有的函数计算皮尔逊相关系数：

coeff = corr(X , Y);

4、参考内容

http://zh.wikipedia.org/zh-cn/%E7%9B%B8%E5%85%B3