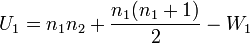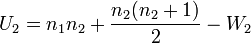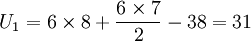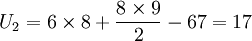曼慧尼特u检验（两个样本数据间有无差异）

曼-惠特尼U检验（Mann-Whitney检验）

How the Mann-Whitney test works

Mann-Whitney检验又叫做秩和检验，是比较没有配对的两个独立样本的非参数检验。思想是这样的：假定要检验两组数据之间有没有差异。首先，不管分组把所有数据排序。按照数值大小给定一个值叫做秩。最小的值秩为1，最大的为N（假定两个样本总共有N个观察值）。如果有相同的值，就得到相同的秩。相同的值的秩是他们的秩的平均值。如果两组的秩的和差距比较大，就会得出较小的p值，认为这两组间有显著差异。

How to think about the results of a Mann-Whitney test

样本量太小的话效度会很低。比如，如果总的数据只有7个或者更少的话，p值总是大于5%的。

Is the Mann-Whitney test the right test for these data?

分析之前要先看一下，Mann-Whitney 检验是否适合手头的问题。

问题	解释
“误差”是独立的吗？	“误差”指的是每个值和中位数的差异。仅当误差的分布是随机的时候Mann-Whitney 检验的结果才有意义。一般要保证独立样本。样本不独立可能会导致误差不随机。
数据是配对的吗？	如果数据是配对的，应该用Wilcoxon成对检验。
是只比较两组数据吗？	Mann-Whitney 检验只用于两组数据的比较。如果要比较多组数据，可以用 Kruskal-Wallis 检验。用几次 Mann-Whitney 检验来比较多个组间的差异是不适合的，就如同ANOVA 不能用多次t检验代替一样。
两个分布的形状是相同的吗？	Mann-Whitney 检验不需要假定数据符合某种分布，但是要求两个分布是相同的。如果两组的分布差异比较大，可能需要数据转换使之相近。
是否比较中位数？	Mann-Whitney 检验比较的是两组的中位数。
数据分布时正态的吗？	非参数检验的好处和弱点是不需要假定数据符合某种分布。非参数检验有时候更适合（当数据分布未知时），有时候效度较低（当已知分布时参数检验效度更高）。所以如果数据能够转换为正态分布，t检验将会有更高的效度。

曼-惠特尼U检验的步骤

Computation of the U test begins by arbitrarily designating two samples as group 1 and group 2.the data from the two groups are combined into one group ,with each data value retaining a group identifier of its original group.the pooled values are then ranked from 1 to n,with the smallest value being assigned a rank of 1.

The sum of the ranks of Values from group 1 is computed and designated as W1 and the sum of the ranks of values from group 2 is designated as W2.^[1]

　　该方法的具体步骤如下：

　　第一步：将两组数据混合，并按照大小顺序编排等级。最小的数据等级为1，第二小的数据等级为2，以此类推（若有数据相等的情形，则取这几个数据排序的平均值作为其等级）。

　　第二步：分别求出两个样本的等级和W₁、W₂。

　　第三步：计算曼-惠特尼U检验统计量，n₁为第一个样本的量，n₂为第二个样本的量：

　　选择U₁和U₂中最小者与临界值U_α比较，当U < U_A时，拒绝H₀，接受H₁。

　　在原假设为真的情况下，随机变量U的均值和方差分别为：

　　　　

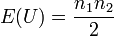
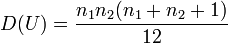
　　当n₁和n₂都不小于10时，随机变量近似服从正态分布。

　　第四步：作出判断。

　　设第一个总体的均值为μ₁，第二个总体的均值为μ₂，则有：

　　1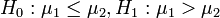），如果Z < − Z_α，则拒绝H₀；

　　2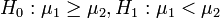），如果Z > Z_α，则拒绝H₀；

　　3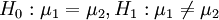），如果Z > − Z_alpha / 2，则拒绝H₀。

[编辑]

曼-惠特尼U检验的应用举例

　　下面是两种不同加工方式的菜粕在黄牛瘤胃内培养16h的干物质降解率，用曼-惠特尼U检验比较其有无差异：

　　　　　　两种加工方式的菜粕瘤胃培养16h的干物质降解率(%)

预压浸出组	等级排序	螺旋热榨组	等级排序
39.33	3	42.91	5
44.10	8	44.69	10
35.89	1	44.54	9
43.35	6	45.31	11
47.61	13	37.73	2
43.71	7	48.75	14
		46.71	12
		41.85	4

　　先按照大小顺序排列等级(见上表)，而后计算W₁ = 38,W₂ = 67,n₁ = 6,n₂ = 8。

　　假设两种菜粕的16h瘤胃干物质降解率除了平均水平以外在其它方面无差异，即检验：

H₀：两种菜粕的16h瘤胃干物质降解率无差异；

H₁：两种菜粕的16h瘤胃干物质降解率有差异。

　　计算U值：

　　U₂值较小，选取U₂与U_α(α=0.05)比较，通过查表(附表)可知U_α = 8,U₂ > U_α，即接受H₀，认为两种加工方式的菜粕瘤胃培养16h的干物质降解率无显著差异。

　

n2	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
n1
1
2								0	0	0	0	1	1	1	1
3					0	1	1	2	2	3	3	4	4	5	5
4				0	1	2	3	4	4	5	6	7	8	9	10
5			0	1	2	3	5	6	7	8	9	11	12	13	14
6			1	2	3	5	6	8	10	11	13	14	16	17	19
7			1	3	5	6	8	10	12	14	16	18	20	22	24
8		0	2	4	6	8	10	13	15	17	19	22	24	26	29
9		0	2	4	7	10	12	15	17	20	23	26	28	31	34
10		0	3	5	8	11	14	17	20	23	26	29	33	36	39
11		0	3	6	9	13	16	19	23	26	30	33	37	40	44
12		1	4	7	11	14	18	22	26	29	33	37	41	45	49
13		1	4	8	12	16	20	24	28	33	37	41	45	50	54
14		1	5	9	13	17	22	26	31	36	40	45	50	55	59
15		1	5	10	14	19	24	29	34	39	44	49	54	59	64

n2	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
n1
1
2								0	0	0	0	1	1	1	1
3					0	1	1	2	2	3	3	4	4	5	5
4				0	1	2	3	4	4	5	6	7	8	9	10
5			0	1	2	3	5	6	7	8	9	11	12	13	14
6			1	2	3	5	6	8	10	11	13	14	16	17	19
7			1	3	5	6	8	10	12	14	16	18	20	22	24
8		0	2	4	6	8	10	13	15	17	19	22	24	26	29
9		0	2	4	7	10	12	15	17	20	23	26	28	31	34
10		0	3	5	8	11	14	17	20	23	26	29	33	36	39
11		0	3	6	9	13	16	19	23	26	30	33	37	40	44
12		1	4	7	11	14	18	22	26	29	33	37	41	45	49
13		1	4	8	12	16	20	24	28	33	37	41	45	50	54
14		1	5	9	13	17	22	26	31	36	40	45	50	55	59
15		1	5	10	14	19	24	29	34	39	44	49	54	59	64

n2	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
n1
1
2								0	0	0	0	1	1	1	1
3					0	1	1	2	2	3	3	4	4	5	5
4				0	1	2	3	4	4	5	6	7	8	9	10
5			0	1	2	3	5	6	7	8	9	11	12	13	14
6			1	2	3	5	6	8	10	11	13	14	16	17	19
7			1	3	5	6	8	10	12	14	16	18	20	22	24
8		0	2	4	6	8	10	13	15	17	19	22	24	26	29
9		0	2	4	7	10	12	15	17	20	23	26	28	31	34
10		0	3	5	8	11	14	17	20	23	26	29	33	36	39
11		0	3	6	9	13	16	19	23	26	30	33	37	40	44
12		1	4	7	11	14	18	22	26	29	33	37	41	45	49
13		1	4	8	12	16	20	24	28	33	37	41	45	50	54
14		1	5	9	13	17	22	26	31	36	40	45	50	55	59
15		1	5	10	14	19	24	29	34	39	44	49	54	59	64