转自:https://blog.csdn.net/sparkkkk/article/details/72598041,感谢分享!
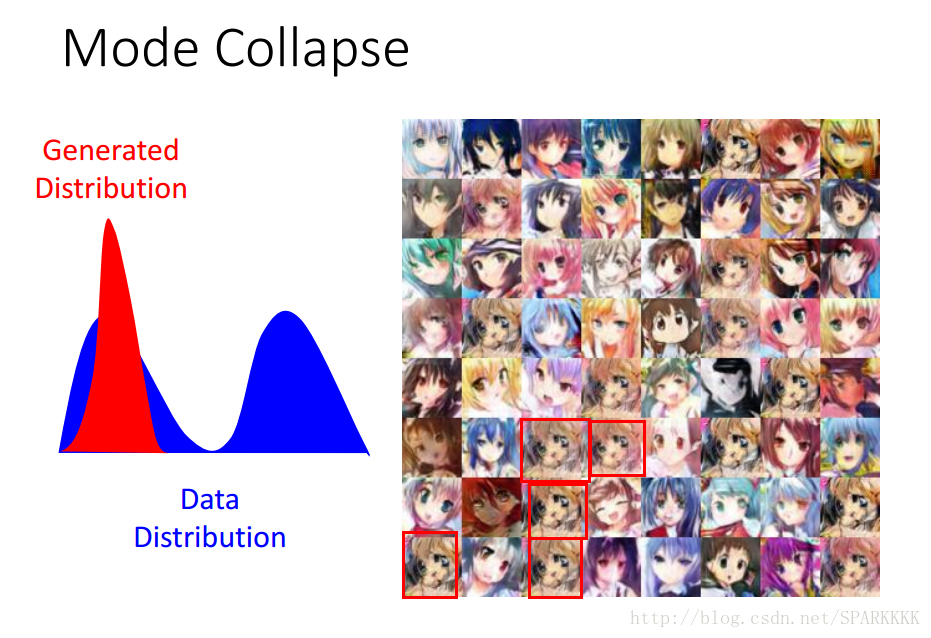
先给一个直观的例子,这个是在我们训练GAN的时候经常出现的
这就是所谓的Mode Collapse
但是实际中ModeCollapse不能像这个一样这么容易被发现(sample中出现完全一模一样的图片)
例如训练集有很多种类别(如猫狗牛羊),但是我们只能生成狗(或猫或牛或羊),虽然生成的狗的图片质量特别好,但是!整个G就只能生成狗,根本没法生成猫牛羊,陷入一种训练结果不好的状态。这和我们对GAN的预期是相悖的。

如上图。PdataPdata是八个高斯分布的点,也就是8个mode。
我们希望给定一个随机高斯分布(中间列中的最左图),我们希望这一个随机高斯分布经过G最后可以映射到这8个高斯分布的mode上面去
但是最下面一列的图表明,我们不能映射到这8个高斯分布的mode上面,整个G只能生成同一个mode,由于G和D的对抗关系,G不断切换mode
李宏毅原话:
在step10k的时候,G的位置在某一个 Gaussian所在位置,然后D发现G只是在这个Gaussian这里了,所以就把这个地方的所有data(无论real还是fake)都给判定为fake
G发现在这个Gaussian待不下去了,只会被D永远判定为fake,所以就想着换到另一个地方。在step15k就跳到了另一个Gaussian上去
然后不断跳跳跳,不断重复上述两个过程,就像猫捉老鼠的过程一样,然后就没有办法停下来,没法达到我们理想中映射到8个不同的Gaussian上面去
为什么会出现模式坍塌
参考资料:https://blog.csdn.net/Forlogen/article/details/89608973
李宏毅原话:
在step10k的时候,G的位置在某一个 Gaussian所在位置,然后D发现G只是在这个Gaussian这里了,所以就把这个地方的所有data(无论real还是fake)都给判定为fake
G发现在这个Gaussian待不下去了,只会被D永远判定为fake,所以就想着换到另一个地方。在step15k就跳到了另一个Gaussian上去
然后不断跳跳跳,不断重复上述两个过程,就像猫捉老鼠的过程一样,然后就没有办法停下来,没法达到我们理想中映射到8个不同的Gaussian上面去
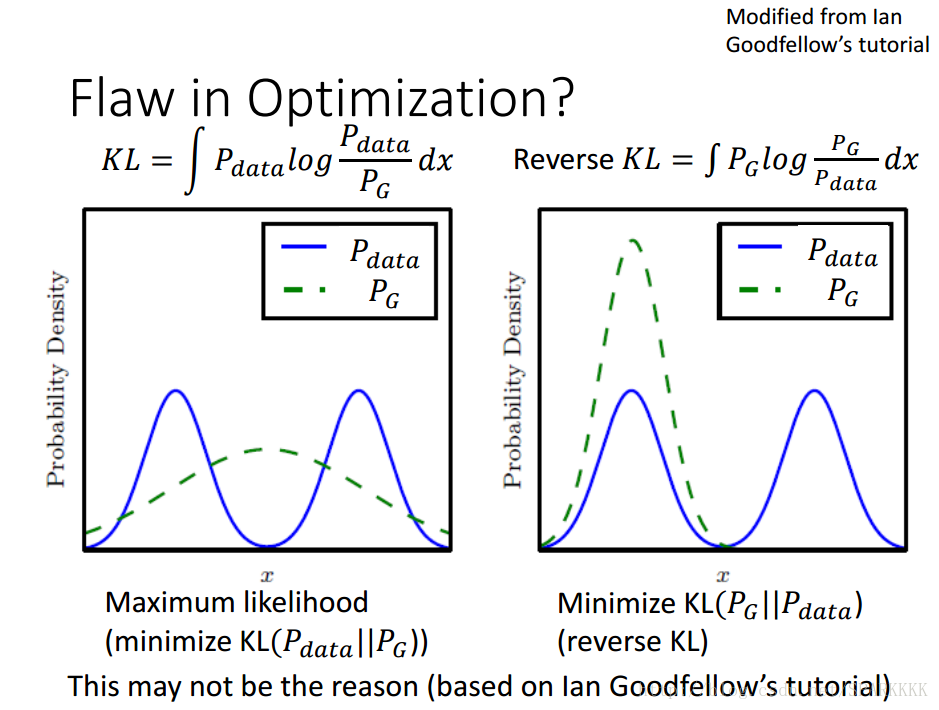
对于左边的KL散度,出现无穷大的KL散度是因为PdataPdata有值而PGPG没有值
也就是说当我们PdataPdata有值的时候,我们必须保证PGPG也有值,这才能保证KL散度不会趋于无穷大。
假设我们的G的capacity不够,只能产生一个Gaussian的时候,那么这个时候的G就会倾向去覆盖所有PdataPdata存在的地方,PdataPdata有值的地方PGPG也要有。
当然,即使PdataPdata没有的地方,有PGPG也无所谓(毕竟这个时候KL散度趋于0,惩罚很小)
虽然这个时候基本上不会出现mode collapse的情况,但是会出现很多无意义的样本
对于右边的reverse KL散度,如果出现了PGPG在某一个没有PdataPdata(Pdata≈0Pdata≈0)的位置产生了值,那就会使得这个reverse KL散度变得特别大。
所以对于在minimize KL散度这个training过程中,就会出现很高的惩罚。为了安全起见,PGPG就会更加倾向于生成同一张安全的一定会被认为是real的image,也不冒险去产生一些不一样的image
而由于我们这里假设PGPG只是一个单一的Gaussian而不是多个Gaussian叠加(如图中的PdataPdata),所以就会趋向于去完全拟合其中一个真实的Gaussian,这样就出现了mode collapse