类偏斜的误差度量
比如在一个肿瘤预测的问题上,当大量的样本为负样本(实际上没有肿瘤99.5%),只有少数的样本为正样本(实际存在肿瘤0.5%)。那么评判一个机器学习模型的指标,就需要调整。
在一个极端的情况,当一个模型为y=0,也就是将所有预测全为负样本,就有了99.5%的正确率,而这种模型忽略了输入,相比于一个良好的模型,本来应该能够预测出一些肿瘤的情况。所以,前者极端的模型,是没有意义的。因此,引入查准率(precision)和查全率(recall)。
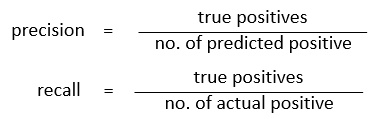
查准率指的是:在所有预测为正样本的结果中,实际上为正样本的比率。TP/(TP+FP)
查全率指的是:在所有实际为正样本的结果中,预测值为正样本的比率。TP/(TP+FN)
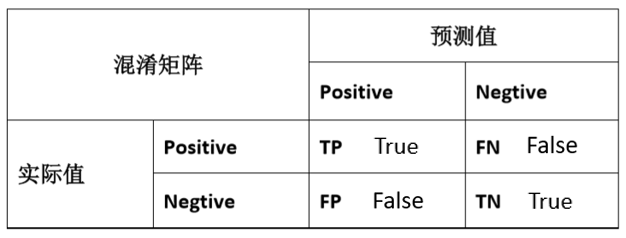
这样的度量方法,在类偏斜方面的,机器学习模型,效果会好一点。不论是查准率或者查全率,当然是越高越好。一般将正样本作为少数类,便于概念统一。以这样的方法度量,极端模型上的查准率和查全率,都为0了。
查准率和查全率之前的权衡
查准率越高,则当预测为正样本后,该预测的实际为正样本,可靠性越高。模型注重一旦预测为正样本,实际就应是正样本。
查全率越高,则该模型对于实际上应该为正样本的条目,预测结果也为正样本,可靠性越高。模型注重,一旦做出判断,该判断的结果集,就应该包含了,尽可能多的实际应该为正样本的条目。
在查准率和查全率做权衡时,使用均值的方案是不可靠的,尤其是算法1和算法3,当使用均值度量,则比较不出结果。使用F1 score的方法,应该是更好的。
分数越高越好,这样可以看,当查准,查全都是1,F1 score也为1,就是最好的结果。

机器学习中的数据
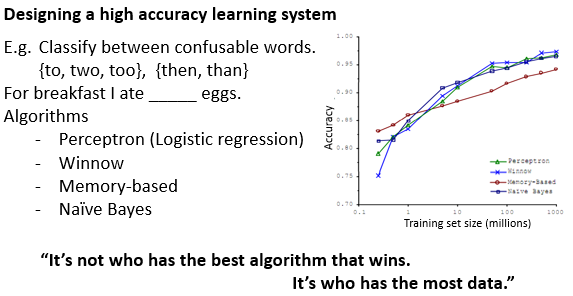
机器学习系统中的算法,有不少都是随着数据量的增大而变优的。这样的原理是,训练集越多,也不容易过拟合(高方差),因为训练误差会更接近测试误差。对于欠拟合问题(高偏差),也对应使用更多的参数和数据解决了。
或者说,更多的训练模型参数,更多的数据特征,学到更多,而输出结果和这些数据中的更多特征有关系吧。
优化目标
为了说明支持向量机SVM的模型构成,说明一下从逻辑回归,到SVM的演变。
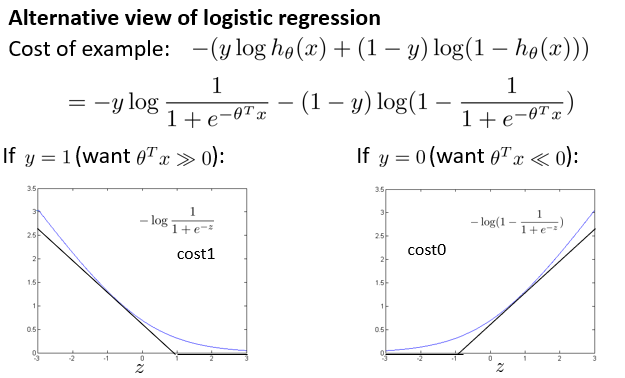
逻辑回归的假设函数h如下,其中,回归模型中的theta与x的乘积得出后,做了非线性变换,得到h的结果。
图中可以看到,表示z的值,与函数h的输出关系,用于预测结果为1(正样本)或者为0(负样本)。

逻辑回归的代价函数cost如下,其中省略了求和与1/m的部分,还有theta正则化等。通过代价函数的最小化,来训练模型中的theta值。
其中的对数部分,是一条曲线,用于降低或者消除局部最优的效果(应该是之前提到过的)。在支持向量机中,使用折线cost函数取代了对数部分。
下面是逻辑回归代价函数和支持向量机的目标函数对比。首先是cost1和cost0的部分,做了替换。
然后是将1/m的部分去掉了。去掉的原因是:在支持向量机中,为了求得式子的最小值,而式子乘除一个常数,最终求得的结果的目标值theta值,应该是不变的。(但是整个式子的值是变了,就是cost本身的大小是变了)
另外修改了lambda的位置到了前项C中。C的控制效果和逻辑回归是一致的,C越小,则类似lambda越大,正则化效果越明显。C置于前项的目的是,思维方式上,更注重前项带来的影响。
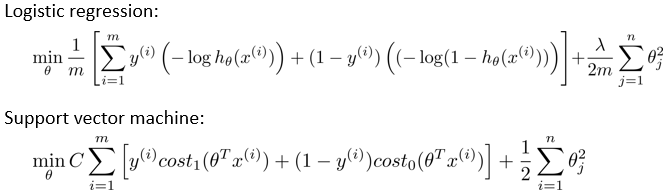
好了,支持向量机的目标函数(也可以说是代价函数吧),在上面的给出了。但是和逻辑回归中使用sigmoid函数得出假设函数(预测函数)h不一样,支持向量机的h函数,是从目标函数中得出的。
最小化目标函数后,若thetaX>=0,则输出h为1,否则输出h为0。
大边界的直观理解
支持向量机的大边界,指的是划分类以后,中间空出的距离。
在实际划分类的时候,使用h函数,当thetaX大于等于0,即可判定该数据为正样本1。但是对应的目标函数(误差函数)来说,仍然存在误差,若果thetaX>=1,则误差才为0。
同理y=0的情况。也就是说,支持向量机在-1和1之间的thetaX上,保留了一定的安全距离。

当C的值越大的时候,支持向量机的目标函数更侧重于第一项的安全距离,所以在下图中,更侧重于黑线的决策边界。其中蓝色为间距。
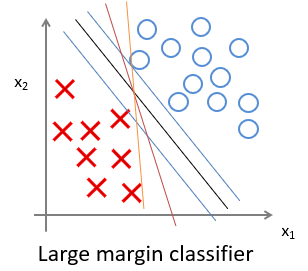
但是极端的C过大,往往会导致一些数据干扰也学习,效果变差。更好的方法是降低C值,这样将边界从蓝线变到黑线处。
当C不是非常非常大的时候,它可以忽略掉一些异常点的影响,得到更好的决策界。(C 较大时,相当于逻辑回归中的lambda 较小,theta影响增强,可能会导致过拟合,高方差。当theta影响减低,就会忽略一些干扰项)

大边界分类背后的数学
向量内积
uT * v = u1*v1+u2*v2 = (u1^2+u2^2)*exp(1/2) * p。其中,p为v向量在u向量上的投影,可以为负。 (u1^2+u2^2)*exp(1/2) 为u向量的长度,记做||u||,为u的范数。
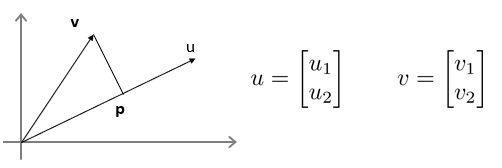
在支持向量机的目标函数中,当C过大,而要求式子为最小化时候,认为前项值则为0,则可以将目标函数简化为如下形式,这时候只要求theta最小。
而theta可以写作范数形式:1/2(||theta||^2)。那么这时候对于目标函数的要求是,让theta代表的范数(或者成为theta的长度)最小。
![]()
其实,在之前的讨论中,当thetaT * X >=1,输出的h函数值为1,且目标函数为最小(为0)。thetaT * X <= -1 ,输出h函数值为0,目标函数最小(为0)。
通过向量内积公式得到: thetaT * X = p * ||theta||,因此有如下的关系。
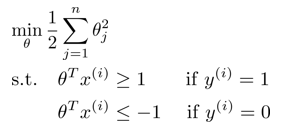
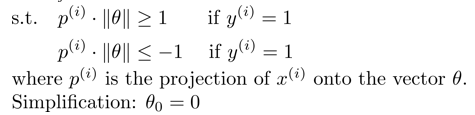
在如下两种分类边界上,蓝线为边界,黑色箭头为theta的方向(这里假设theta过原点的)。
在第一中情况下,thetaT * x的值,表示为p * ||theta||,要得到正样本的h为1的输出,则要求p * ||theta||>=1,theta在目标函数中,要求了最小化,则p需要增大,才能获得输出1。p为样本在theta向量的投影。
而第二种情况下,p样本在theta向量上的投影更长,在theta不够大的情况下,更能够使得p * ||theta||>=1,获得正样本输出。支持向量机的原理,就是寻找使得p更大的theta方向,同时theta的值(范数)足够小。

核函数1
考虑如下的二分类问题,需要一个更好的模型,才能够更正确的分类。而x的特征之间组合形式多种多样。一个个模型尝试(之前也许有提到)虽然是一种方法,但是低效,耗费计算能力。
所以,使用了,高斯核函数,选定地标,然后对于输入样本,计算和地标之间的相似性,判定分类结果。
高斯核函数如下f1,其内部||x-l||,为样本x与地标l的距离。距离越近,则f1输出越接近1,越远则接近0,其中cegma控制了核函数的宽窄。
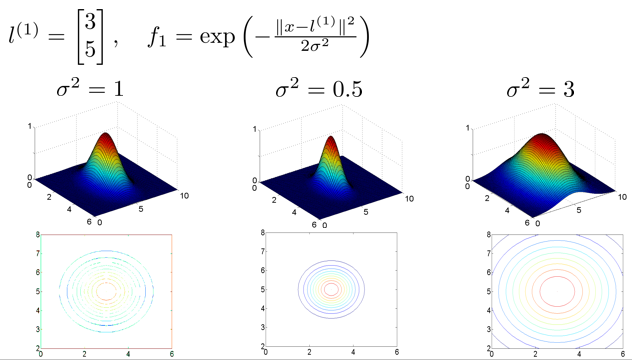
在如下三个地标上,令theta0=-0.5,theta1=1,theta2=1,theta3=0。则有如下效果:
当样本x,接近l1,l2,获得0.5,则认为是正样本输出,对应的输出预测为1。而接近l3,获得-0.5,对应预测输出0,谁也不接近,则预测输出0。
