Octave操作概览


hold on
legend('sin','cos')
title('myplot')
plot(t,y2,’r’)
xlabel('time')
ylabel('value')
print –dpng 'myplot.png' 保存图像
figure(1)
plot(t, y1)
figure(2)
plot(t, y2)
subplot(1,2,1)
plot(t,y1)
subplot(1,2,2)
plot(t,y2)
axis([0.5 1 -1 1]) 设置x轴和y轴的范围
Clf 清除图像
imagesc(A),colorbar,colormap gray 生成方阵图
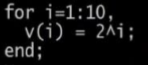
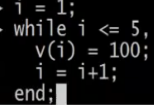
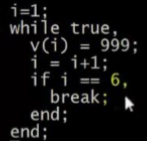
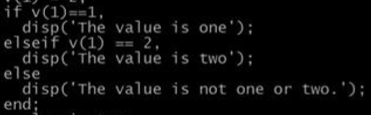
向量化

向量化乘法可以帮助更快更直接的运行乘法并求和。将之前的分别乘法并求和直接转换为一步的矩阵乘法。
从而可以使用向量化的方法计算theta。
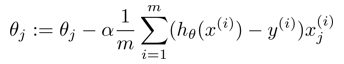
逻辑回归
使用0表示负类,1表示正类。输出值在0到1之间,属于一种分类算法。
线性回归中,预测值可以超出0-1的范围,不适合解决分类的问题,应用上因数据影响也容易出错。
逻辑回归中,限制输出在0-1之间,引入sigmod函数,套在预测输出h外。
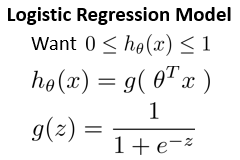
决策边界
在进行分类过程中,建立的模型对分类问题影响很大,不同次方形式的表达式,适应不同特点的数据集。


代价函数
逻辑回归中代价函数J定义为:
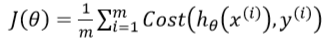
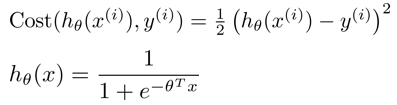
但是其中引入的h函数,使得代价函数J是一个非凸函数?有多个极小值点。
更改其中的cost函数为:
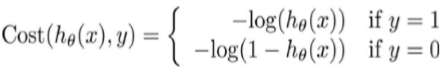
变形:
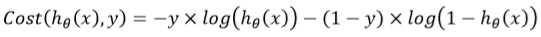
综合:



